Что такое отрицательная степень числа в математике
Содержимое
- 1 Что такое отрицательная степень числа в математике
- 1.1 Что такое отрицательная степень числа?
- 1.2 Понятие отрицательной степени числа
- 1.3 Как вычислить отрицательную степень числа?
- 1.4 Зачем нужна отрицательная степень числа?
- 1.5 Примеры отрицательной степени числа
- 1.6 Отрицательная степень и десятичная форма
- 1.7 Отрицательная степень и умножение
- 1.8 Отрицательная степень и деление
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
Отрицательная степень числа в математике – это способ записи десятичной дроби с использованием отрицательного показателя степени. Узнайте, как работает отрицательная степень и как выполнять операции с числами в такой форме.
Отрицательная степень числа — одно из основных понятий в математике, которое часто используется в различных областях науки и повседневной жизни. Для понимания этого понятия необходимо иметь представление о понятии степени числа.
Степень числа — это результат возведения данного числа в некоторую степень. Если степень положительная, то это означает, что число умножается само на себя несколько раз. Например, число 2 в степени 3 равно 2 * 2 * 2 = 8.
Однако, когда степень числа отрицательная, происходит обратная операция — число делится на себя несколько раз. Например, число 2 в степени -3 равно 1 / (2 * 2 * 2) = 1/8 = 0.125.
Отрицательная степень числа имеет свои особенности и правила, согласно которым она вычисляется. Например, если число a возвести в степень -n, то результат будет равен 1 / (a^n).
Отрицательная степень числа находит применение в различных областях науки, таких как физика, экономика, компьютерные науки и другие. Например, в физике отрицательная степень может использоваться для описания десятичных долей, которые меньше единицы. В экономике она может быть использована для определения коэффициента убывания цен на товары.
Что такое отрицательная степень числа?
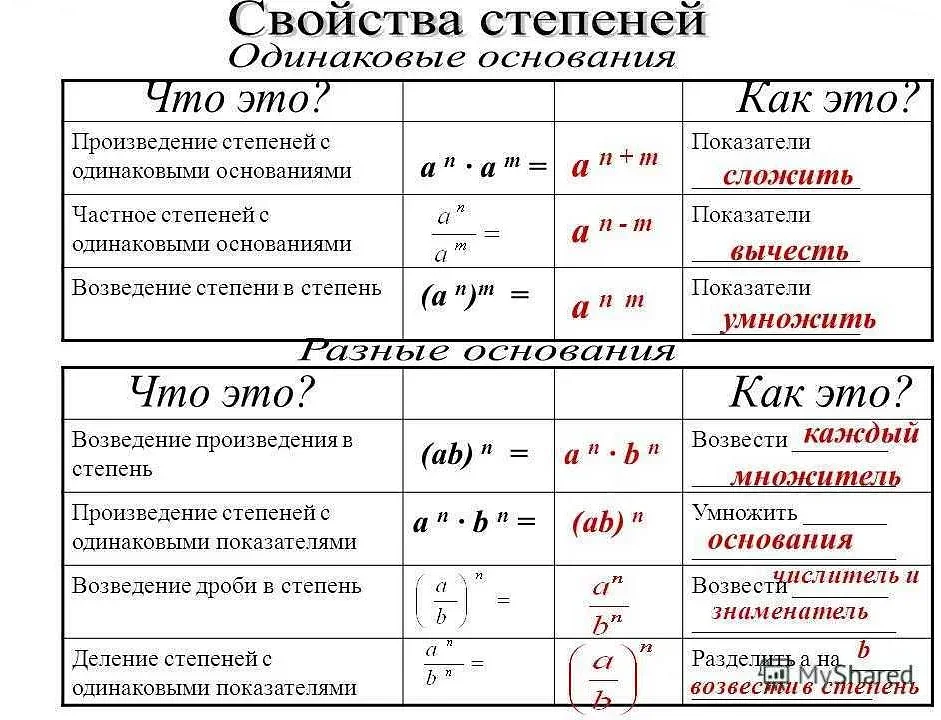
Например, если рассмотреть число 2, то его отрицательные степени будут 1/2, 1/4, 1/8 и так далее. Это означает, что если возвести число 2 в степень 1/2, то получится квадратный корень из 2, возвести в степень 1/4 — получится четвертый корень из 2, и так далее.
Отрицательные степени чисел также используются в математике для обозначения обратных величин. Например, если число 2 возвести в степень -1, то получится 1/2, что является обратной величиной числа 2.
Понятие отрицательной степени числа
Отрицательная степень числа представляет собой математическое понятие, которое определяет, какую дробь образует число, возведенное в отрицательную степень. Если число a возведено в отрицательную степень -n, то результатом будет дробь, равная единице, деленной на число a, возведенное в положительную степень n. Другими словами, a^(-n) = 1/(a^n).
Для примера, рассмотрим число 2, возведенное в отрицательную степень -3. Согласно определению, это будет равно 1/(2^3) = 1/8 = 0.125.
Отрицательная степень числа имеет свои особенности. Например, a^(-n) всегда будет являться дробью, даже если число a — целое или действительное. В таком случае, дробь будет иметь знаменатель равный 1, а числитель — результат возведения числа a в положительную степень n.
Отрицательная степень числа находит применение в различных областях математики и физики, например, при решении задач, связанных с отрицательными величинами, показателями и коэффициентами. Отрицательная степень числа позволяет обращать числа или величины и находить обратное значение к исходному.
Как вычислить отрицательную степень числа?
Отрицательная степень числа представляет собой взятие обратного значения числа и возведение его в положительную степень. Для вычисления отрицательной степени числа можно воспользоваться следующей формулой:
a-n = 1 / (an)
Где a — число, а n — положительное число, указывающее степень.
Например, чтобы вычислить отрицательную степень числа 2-3, нужно возвести число 2 в степень 3, а затем взять его обратное значение:
2-3 = 1 / (23) = 1 / 8 = 0.125
Таким образом, отрицательная степень числа дает десятичную дробь, которая является обратным значением числа, возведенного в положительную степень.
Зачем нужна отрицательная степень числа?
В математике отрицательная степень числа играет важную роль, позволяя нам работать с дробными и очень большими числами. Она позволяет нам обобщить понятие степени и расширить его на все действительные числа.
Отрицательная степень числа определяется как обратная величина положительной степени. Например, если число a возводится в степень -n, то это означает, что мы берем обратное значение числа a в степени n. Таким образом, a^-n = 1/(a^n).
Наличие отрицательных степеней числа позволяет нам записывать дробные значения в виде десятичной дроби с отрицательной показательной степенью. Например, число 0.01 можно записать как 1 * 10^(-2), где -2 — отрицательная степень числа 10.
Отрицательная степень числа также позволяет нам работать с очень большими числами. Например, если мы возводим число 10 в отрицательную степень, то получаем очень маленькое число, близкое к нулю. Это может быть полезно при решении задач, связанных с научными и инженерными расчетами, где точность и масштаб чисел играют важную роль.
В заключение, отрицательная степень числа является важным математическим понятием, которое позволяет нам работать с дробными и очень маленькими числами, а также упрощает запись и вычисления различных математических формул.
Примеры отрицательной степени числа

Отрицательная степень числа представляет собой десятичную дробь, полученную путем деления единицы на это число, возведенное в положительную степень.
Например, если мы возведем число 2 в отрицательную степень, то получим:
- 2-1 = 1/2 = 0.5
- 2-2 = 1/(2*2) = 1/4 = 0.25
- 2-3 = 1/(2*2*2) = 1/8 = 0.125
Таким образом, чем больше отрицательная степень числа, тем меньше результат.
Аналогично, можно вычислить отрицательную степень других чисел. Например:
- 3-1 = 1/3 = 0.3333…
- 10-2 = 1/(10*10) = 1/100 = 0.01
- 5-3 = 1/(5*5*5) = 1/125 = 0.008
Отрицательная степень числа является важным понятием в математике и широко применяется в научных и инженерных расчетах.
Отрицательная степень и десятичная форма
Например, если основание степени равно 10, то число в отрицательной степени будет иметь форму десятичной дроби. Например, 10 в отрицательной второй степени будет равно 0.01, а 10 в отрицательной третьей степени будет равно 0.001. Возведение числа в отрицательную степень значит, что число будет делиться на основание степени.
Отрицательная степень часто используется для представления очень малых значений, которые не могут быть удобно записаны в обычной десятичной форме. Например, скорость света в вакууме равна приблизительно 299792458 метров в секунду. Вместо использования такого большого числа, скорость света в вакууме можно записать как 2.99792458 x 10-8 метров в секунду.
Отрицательная степеньДесятичная форма
| 10-1 | 0.1 |
| 10-2 | 0.01 |
| 10-3 | 0.001 |
| 10-4 | 0.0001 |
Таким образом, отрицательная степень числа позволяет удобно представлять очень малые значения в математике и науке.
Отрицательная степень и умножение
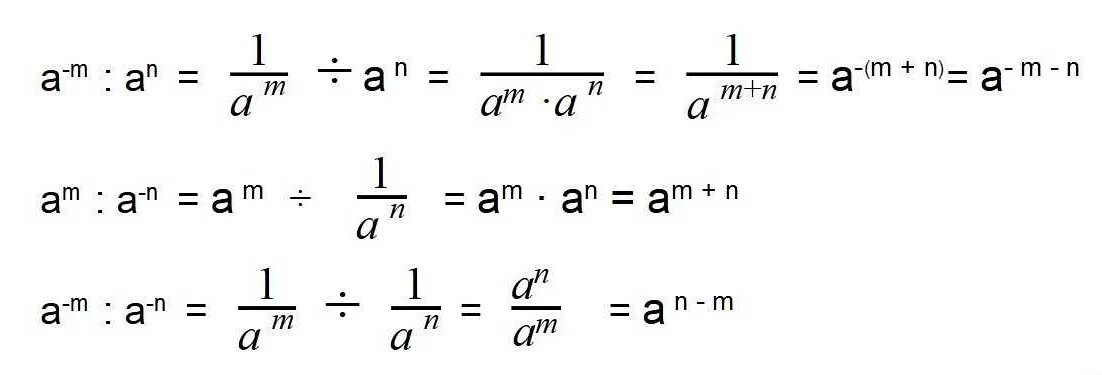
При умножении числа на себя несколько раз (возводя в степень), мы получаем число, равное произведению всех этих множителей. Например, $2^3$ означает, что число 2 нужно умножить на себя 3 раза: $2 \cdot 2 \cdot 2 = 8$.
Если же задана отрицательная степень, то мы получаем дробные значения или числа с десятичной частью. Например, $2^{-3}$ означает, что число 2 нужно умножить на себя 3 раза, но с обратным знаком: $\frac{1}{2 \cdot 2 \cdot 2} = \frac{1}{8} = 0.125$.
Важно помнить, что при умножении на число в отрицательной степени, мы получаем десятичную дробь, которая всегда будет меньше 1. Например, $3^{-2}$ означает, что число 3 нужно умножить на себя 2 раза с обратным знаком: $\frac{1}{3 \cdot 3} = \frac{1}{9} = 0.111\dots$.
Отрицательная степень и умножение являются важными понятиями в математике и находят применение в различных областях, таких как физика, экономика и информатика.
Отрицательная степень и деление
Отрицательная степень числа может быть использована в выражениях, которые связаны с делением. Когда число возводится в отрицательную степень, оно инвертируется и затем возводится в положительную степень.
Например, если имеется число 2, которое необходимо возвести в степень -3, то сначала инвертируем это число, получая 1/2. Затем возводим полученную дробь в положительную степень 3, получая (1/2)^3 = 1/8.
Таким образом, отрицательная степень числа может быть использована для представления обратной величины числа в контексте деления. Это понятие играет важную роль в математике и имеет множество применений в различных областях, таких как физика, экономика и технические науки.
Вопрос-ответ:
Что такое отрицательная степень числа?
Отрицательная степень числа — это математическое выражение, в котором число возводится в отрицательную степень. Например, число 2 в отрицательной степени -2 будет выглядеть как 1/2^2 или 1/4.
Как считать отрицательную степень числа?
Чтобы возвести число в отрицательную степень, нужно взять обратное значение числа и возвести его в положительную степень. Например, чтобы посчитать -2 в степени -3, нужно взять 1/(-2)^3 или -1/8.
Какая формула используется для отрицательной степени числа?
Формула для отрицательной степени числа выглядит следующим образом: a^(-n) = 1/(a^n), где a — число, n — отрицательная степень.
Какие есть примеры отрицательной степени числа?
Примеры отрицательной степени числа в математике: 2^(-2) = 1/2^2 = 1/4, 5^(-3) = 1/5^3 = 1/125, (-3)^(-2) = 1/(-3)^2 = 1/9.
Зачем нужна отрицательная степень числа?
Отрицательная степень числа используется для вычислений, где требуется применение обратного значения числа. Например, в физике и экономике, где нам нужно вычислить обратную величину или решить уравнение, содержащее отрицательные степени чисел.
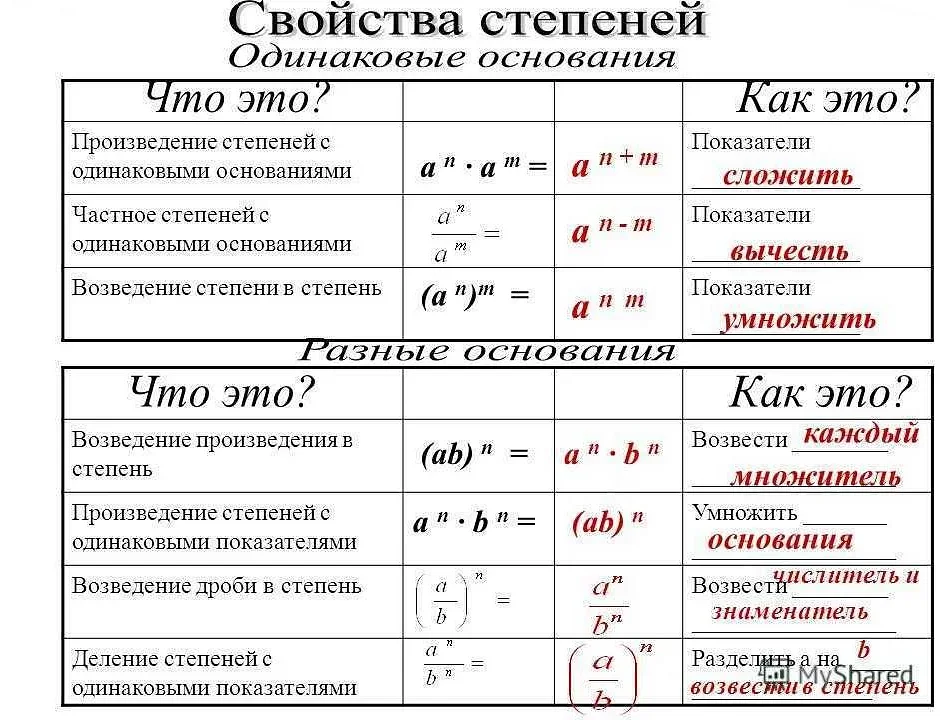



Отрицательная степень числа — это концепция, которая может показаться сложной на первый взгляд. Однако, разобравшись в ней, она становится очевидной и полезной. Например, возведение числа в отрицательную степень эквивалентно нахождению обратного значения этого числа в положительной степени. Это позволяет нам удобно работать с дробными значениями и упрощает математические вычисления. Например, (-2)^-3 равняется -1/8, что означает, что -2 возводится в третью отрицательную степень даст нам обратное значение 1/(-2)^3 или -1/8. Понимание отрицательной степени числа поможет нам освоить сложные математические концепции и применять их в повседневной жизни.
Отрицательная степень числа — это интересное и важное понятие в математике, которое позволяет нам работать с дробными числами и давать им возможность быть меньше единицы. Я всегда задавалась вопросом, как можно числу дать отрицательную степень и что это значит. Оказывается, если число возведено в отрицательную степень, то мы просто берем его обратное значение и возводим в положительную степень. Например, число 2 в степени -3 будет равно 1/2^3, то есть 1/8. Это может показаться немного сложным, но на самом деле это очень полезное и применимое в реальной жизни понятие. Например, в физике мы можем использовать отрицательные степени для обозначения знака величины, например, при описании температуры или заряда. Поэтому, хотя отрицательная степень может показаться непонятной и сложной, она на самом деле очень полезна и помогает нам более точно описывать и понимать мир вокруг нас.
Статья очень понятно объяснила понятие отрицательной степени числа. Я никогда не задумывалась над этим, но теперь все понятно. Примеры также помогли лучше понять материал. Очень полезная информация для школьников и студентов. Буду рекомендовать друзьям!