Что такое степь в математике
Содержимое
Степень в математике — это операция, которая позволяет умножать число на само себя несколько раз. Она играет важную роль в алгебре и арифметике, позволяя решать сложные задачи и находить общие закономерности. Узнайте, как работает степень и как ее применять в различных математических задачах.
Степень — это математическая операция, которая позволяет возводить число в некоторую степень. В степени указывается, сколько раз нужно умножить число на себя. В математической записи степень обозначается в виде числа, называемого основанием, и числа, называемого показателем степени, которое указывается в верхнем правом углу. Например, 2 в степени 3 записывается как 23.
Степень может быть как положительной, так и отрицательной. Положительная степень означает, что число умножается на себя указанное количество раз, а отрицательная степень означает, что число делится на себя указанное количество раз. Например, 2 в степени -2 записывается как 2-2 и равно 1/22 = 1/4.
Степени используются в различных областях математики, физики и инженерии. Например, степени часто используются для вычисления площади круга, объема шара, а также для решения уравнений и построения графиков функций.
Определение степени позволяет более удобно работать с большими числами и упрощает вычисления. Более того, степень является основой для многих других математических операций, таких как корень, логарифм и прогрессия.
Понятие степени в математике
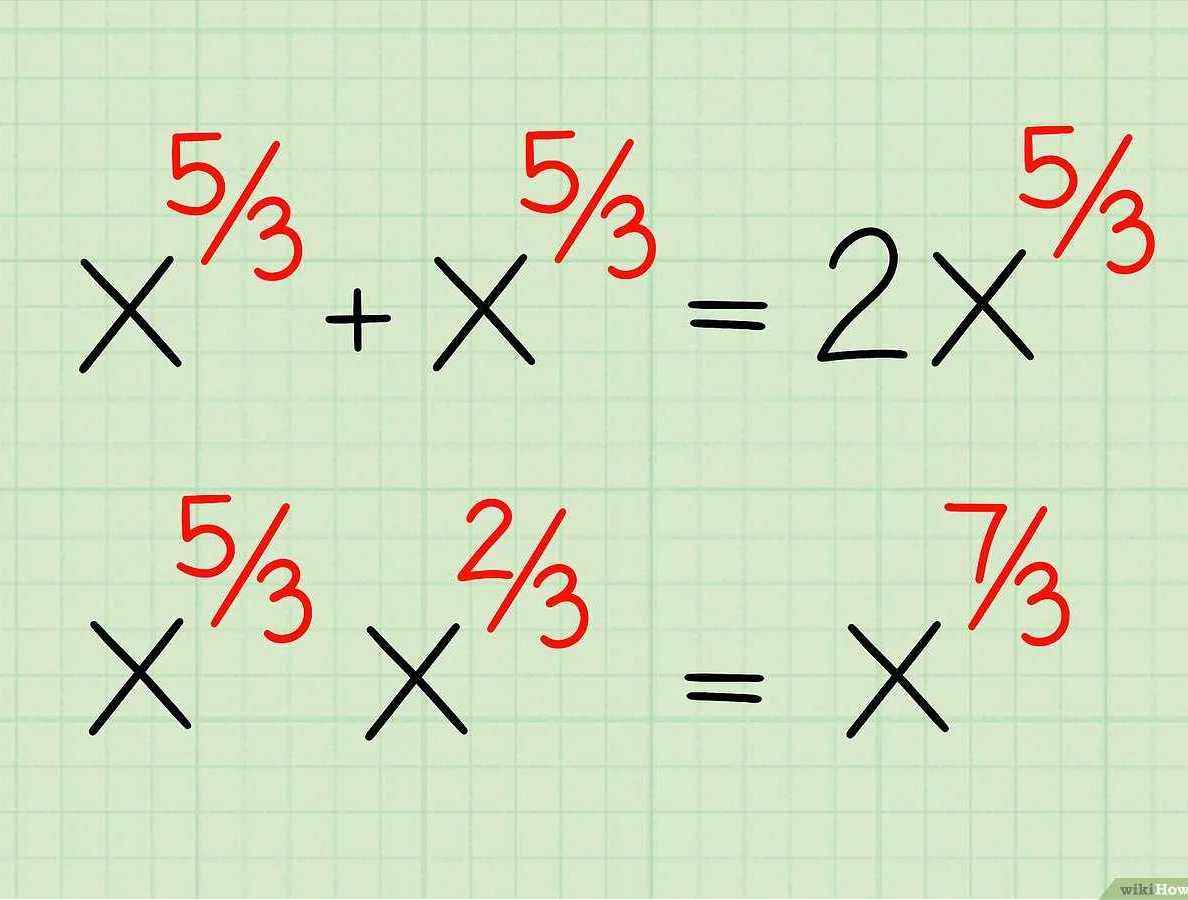
В математике понятие степени используется для обозначения повторного умножения числа на себя. Степень представляет собой способ записи этой операции. Число, которое возводится в степень, называется основанием, а число, на которое оно возводится, называется показателем степени.
Степень обозначается с помощью знака возведения в степень (^), при этом показатель степени записывается в верхнем правом углу основания. Например, числу 2 в степени 3 соответствует запись 2^3.
Степень может быть как положительной, так и отрицательной. Положительная степень означает, что число умножается на себя указанное количество раз. Например, 2^3 равно 2 * 2 * 2 = 8.
Отрицательная степень означает, что число берется в обратном порядке и делится на себя указанное количество раз. Например, 2^-3 равно 1 / (2 * 2 * 2) = 1/8.
Степень может также быть равной нулю. В этом случае любое число, кроме нуля, возводится в степень 0 и равно 1.
Степени широко используются в различных областях математики, физики, экономики и других науках. Они позволяют компактно записывать большие и малые числа, а также решать различные задачи, связанные с повторным умножением или делением чисел.
Основные свойства степеней
1. Свойство умножения степени на степень
Если необходимо умножить две степени с одной и той же основой, то значения степеней складываются, а основа остается неизменной. Например:
am * an = am+n
2. Свойство деления степени на степень
Если необходимо разделить две степени с одной и той же основой, то значения степеней вычитаются, а основа остается неизменной. Например:
am / an = am-n
3. Свойство возведения степени в степень
Если необходимо возвести степень в степень, то значения степеней умножаются. Например:
(am)n = am*n
4. Свойство возведения числа в степень 0
Любое число, кроме нуля, возводится в степень 0, равную 1. Например:
a0 = 1
5. Свойство возведения числа в отрицательную степень
Любое число, кроме нуля, возводится в отрицательную степень путем обращения величины степени и знака числа. Например:
a-n = 1/an
Как вычислить степень числа
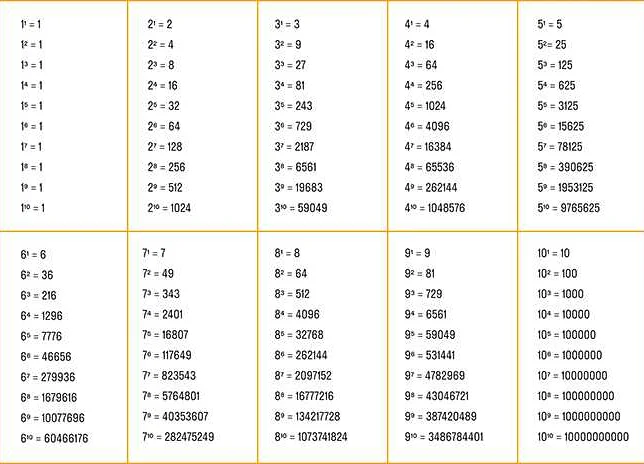
В математике степень числа представляет собой операцию, при которой число умножается само на себя несколько раз. Для вычисления степени числа можно использовать различные методы и алгоритмы.
Один из самых простых способов вычисления степени числа — это повторное умножение числа на себя заданное количество раз. Например, чтобы найти значение 2 в степени 3, нужно умножить число 2 на себя три раза: 2 * 2 * 2 = 8.
Другим способом вычисления степени числа является использование свойства степени, согласно которому a в степени b равно произведению a на само себя b раз. Например, чтобы вычислить значение 2 в степени 4, нужно умножить число 2 на само себя четыре раза: 2 * 2 * 2 * 2 = 16.
В программировании для вычисления степени числа часто используется цикл. Например, в языке программирования Python можно воспользоваться оператором цикла for:
- Задать начальное значение результата равным 1.
- Запустить цикл, в котором число умножается на себя заданное количество раз.
- По окончании цикла, полученное значение будет являться результатом вычисления степени числа.
Например, чтобы вычислить значение 2 в степени 5 в языке Python, можно использовать следующий код:
result = 1
base = 2
exponent = 5
for i in range(exponent):
result *= base
print(result)
В результате выполнения данного кода будет выведено число 32, так как 2 в пятой степени равно 32.
Таким образом, вычисление степени числа может быть выполнено различными способами, включая повторное умножение и использование циклов в программировании.
Примеры степеней

Степень числа может быть как положительной, так и отрицательной. Рассмотрим несколько примеров:
Пример 1: Возведение числа 3 в степень 2:
32 = 3 × 3 = 9
Пример 2: Возведение числа 5 в степень 3:
53 = 5 × 5 × 5 = 125
Пример 3: Возведение числа 2 в степень -4:
2-4 = 1 / (2 × 2 × 2 × 2) = 1/16 = 0.0625
Таким образом, степень числа позволяет умножать число само на себя несколько раз или наоборот, делить число на себя несколько раз, в зависимости от знака степени.
Степень числа с отрицательным показателем
Степень числа с отрицательным показателем определяется следующим образом: если число a не равно нулю, а показатель n является отрицательным целым числом, то a в степени n равно одному делить на a в степени |n|.
Другими словами, если у нас есть число a и отрицательный показатель n, то a в степени n равно 1, деленное на a в положительной степени |n|.
Например, если у нас есть число 2 и показатель -3, то 2 в степени -3 равно 1 деленное на 2 в степени 3, то есть 1/8 или 0.125.
Степень числа с отрицательным показателем позволяет нам работать с дробями и десятичными числами в степени, а также использовать отрицательные показатели для решения различных задач и уравнений. Это важное понятие, которое позволяет нам расширить наши математические возможности и применять их в различных областях.
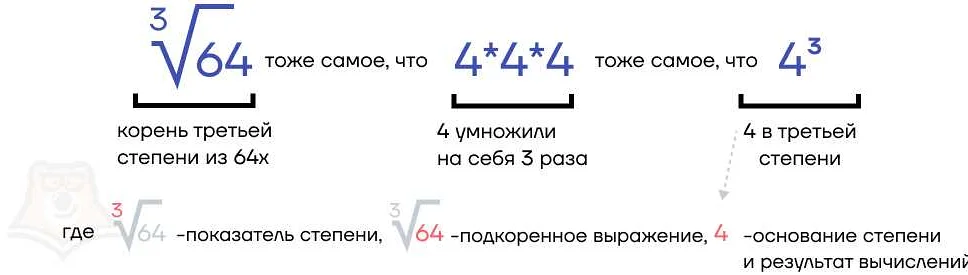
Степень числа с дробным показателем
an = √an
Например, чтобы найти степень числа 2 с показателем 1/2, нужно извлечь квадратный корень из числа 2:
21/2 = √2 ≈ 1.414
Таким образом, степень числа с дробным показателем позволяет находить корни n-й степени из чисел. Эта операция широко используется в различных областях математики, физики и других наук.
Степень числа 0
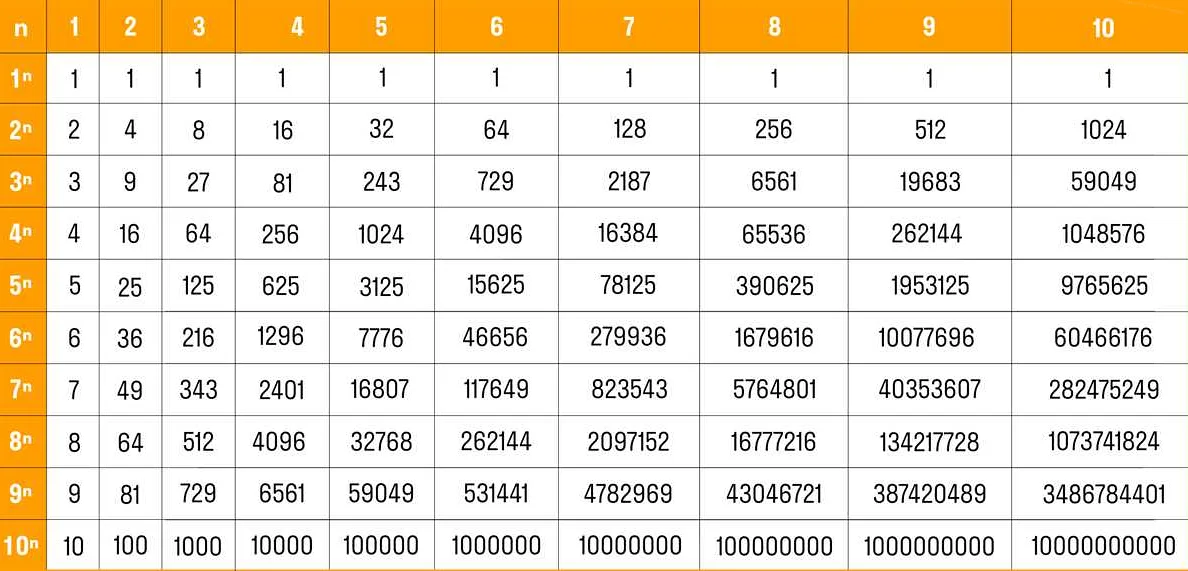
Степенью числа 0 называется результат возведения числа 0 в некоторую степень.
Правила возведения числа 0 в степень:
- 0 в степени 0 не имеет определенного значения и является неопределенностью. Математически это обозначается как 00.
- 0 в положительной степени равно 0: 0n = 0, где n — положительное число.
- 0 в отрицательной степени не имеет определенного значения и является бесконечностью. Математически это обозначается как 0-n.
Степень числа 0 имеет несколько особенностей и может вызывать различные интерпретации в разных математических областях. Ее определение и значение зависит от контекста, в котором она используется.
Например, в алгебре и анализе степень числа 0 считается неопределенной и не имеет значения. Однако в комбинаторике и теории вероятностей степень числа 0 может иметь свое значение, например, как нулевая степень величины.
Вопрос-ответ:
Что такое степень в математике?
Степень в математике — это операция, которая позволяет возводить число в определенную степень. В степень можно возводить как натуральные числа, так и отрицательные и дробные числа. В результате операции степени получается новое число, которое является произведением данного числа на себя заданное количество раз.
Как обозначается степень в математике?
Степень обозначается с помощью знака возвести в степень (^) и числа, которое является показателем степени. Например, 2^3 означает, что число 2 возводится в третью степень.
Какие примеры степеней можно привести?
Примеры степеней в математике могут быть разнообразными. Например, 2^3 = 2 * 2 * 2 = 8. В этом примере число 2 возводится в третью степень, что означает, что оно умножается само на себя три раза. Другой пример: 10^(-2) = 1/10^2 = 1/100. В этом случае число 10 возводится в отрицательную вторую степень, что означает, что его обратное значение умножается само на себя два раза.
Какие правила есть для операции степени?
Для операции степени существуют несколько правил. Например, умножение двух чисел в степени с одинаковым показателем эквивалентно возводить в степень их произведение: (a*b)^n = a^n * b^n. Также существует правило для деления чисел в степени с одинаковым показателем: (a/b)^n = a^n / b^n. Еще одно важное правило — возведение в степень степени: (a^n)^m = a^(n*m).
Как можно использовать степень в реальной жизни?
Степень используется в реальной жизни во многих сферах. Например, в физике для описания явлений, связанных с ускорением, гравитацией и прочими физическими величинами. Также степень применяется в экономике для расчета сложных процентных ставок и прогнозирования роста или спада показателей. В программировании степень используется для выполнения различных математических операций и алгоритмов.
Что такое степь в математике?
Степень в математике — это операция, при которой число (основание) умножается само на себя определенное количество раз (показатель степени). Например, в степени 2 число умножается само на себя один раз: 2^2 = 2 * 2 = 4.
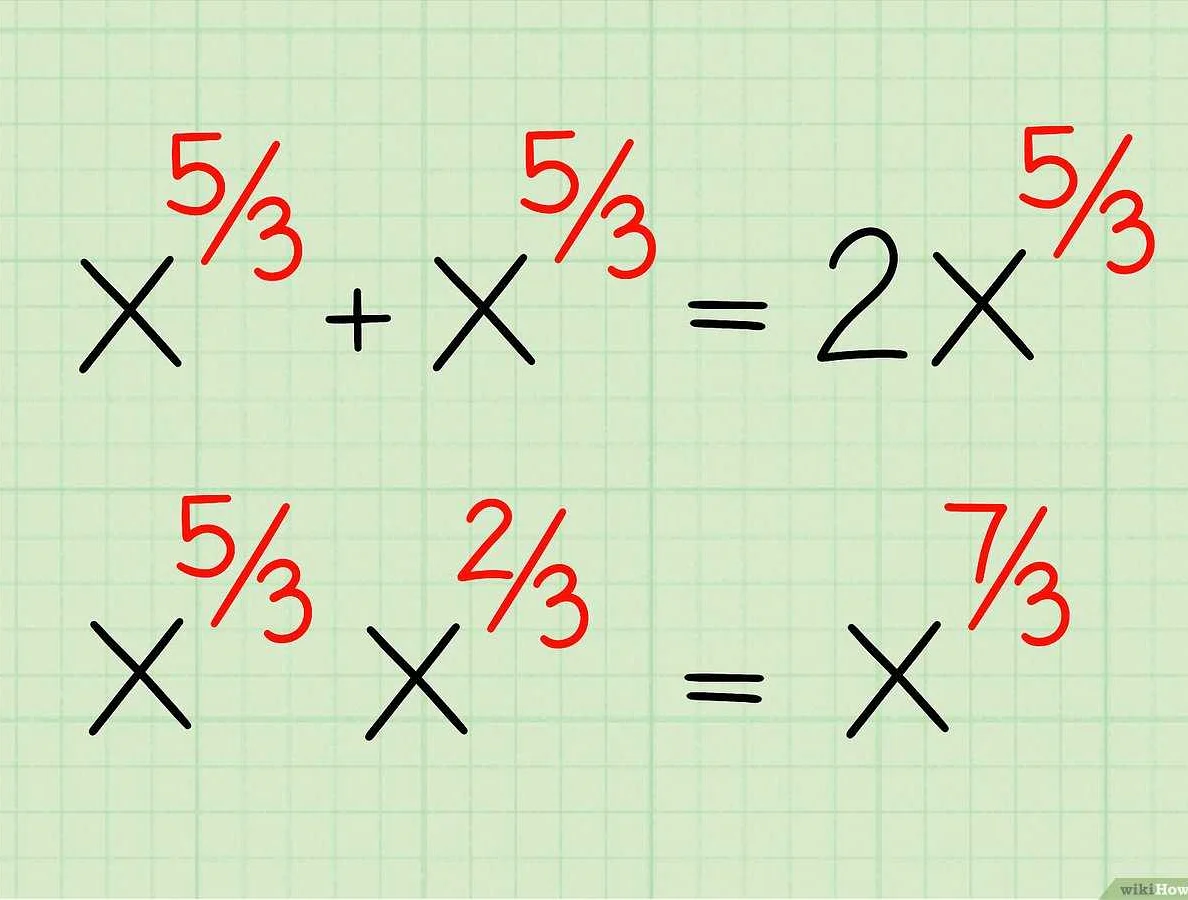
Статья очень понятно и ясно объясняет, что такое степень в математике. Я всегда воспринимал эту концепцию как возведение числа в степень, но теперь я понял, что степень может быть и отрицательной, и дробной. Также, мне очень понравились примеры, которые приведены в статье — они помогли мне лучше усвоить материал. Теперь я точно знаю, что такое степень и как ее использовать в математике. Спасибо за понятное объяснение!