Что означает перевернутый треугольник в математике

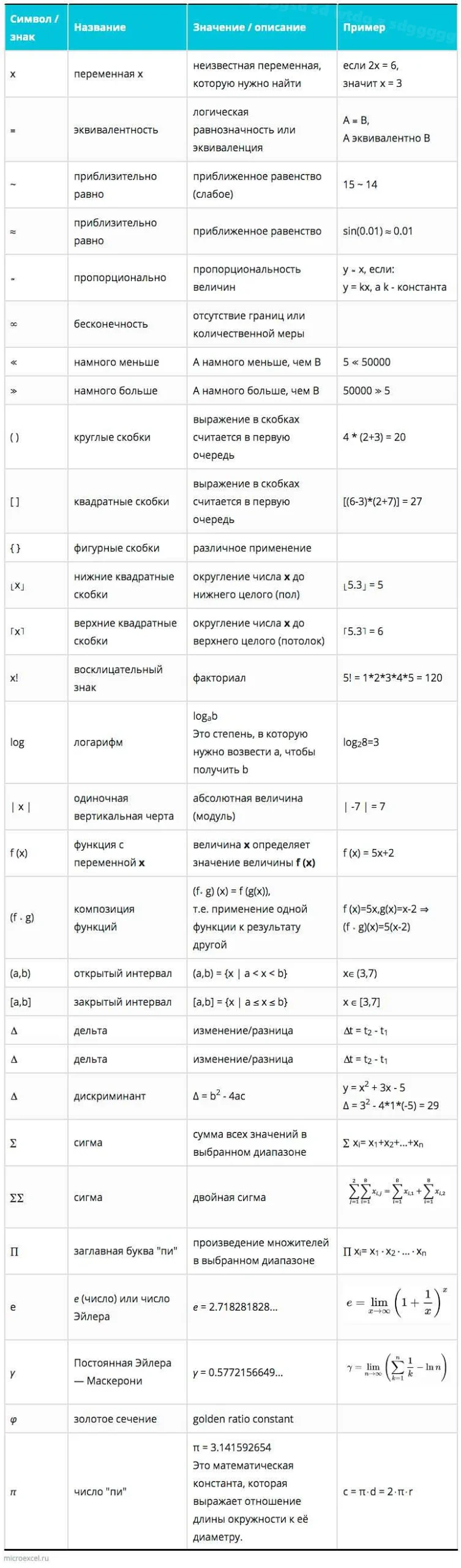
Перевернутый треугольник в математике обозначает отношение противоположности или инверсии. Узнайте, как перевернутый треугольник используется в различных областях математики и какие свойства он имеет.

Перевернутый треугольник — это геометрическая фигура, которая отличается от обычного треугольника тем, что его вершина находится внизу, а основание сверху. Такой треугольник иногда называют «треугольником вверх ногами» или «перевернутым пирамидкой».

Значение перевернутого треугольника в математике состоит в том, что он является одной из основных фигур для изучения геометрии. Он имеет свои характеристики, такие как высота, основание, углы и стороны, которые можно изучать и анализировать. Перевернутый треугольник также является основой для изучения других геометрических фигур, таких как параллелограммы, трапеции и ромбы.

Применение перевернутого треугольника в математике широко распространено. Он используется в решении задач, связанных с расчетами площадей, нахождением длин сторон и углов треугольника, а также определением его геометрических свойств. Кроме того, перевернутый треугольник может быть использован в графическом представлении данных, в программировании и в конструировании различных объектов.

Изучение перевернутого треугольника в математике позволяет углубить понимание геометрии, развить навыки логического мышления и аналитического мышления, а также научиться применять полученные знания на практике.

В заключение, перевернутый треугольник играет важную роль в математике, предоставляя возможность изучать и анализировать геометрические фигуры. Он имеет множество применений в различных областях, требующих расчетов и анализа данных. Изучение перевернутого треугольника помогает развить навыки решения геометрических задач и повысить уровень математической грамотности.

Значение перевернутого треугольника в математике

Перевернутый треугольник часто используется в геометрии и алгебре для решения различных задач. Он позволяет упростить вычисления и упорядочить информацию.

В геометрии, перевернутый треугольник может быть использован для определения площади, периметра и других характеристик фигуры.

В алгебре, перевернутый треугольник может быть использован для решения систем линейных уравнений и нахождения неизвестных значений.

Перевернутый треугольник также имеет символическое значение. Он может служить метафорой для обозначения обратной зависимости или противоположности.

В целом, понимание значения перевернутого треугольника в математике позволяет решать сложные задачи и строить логические цепочки.

Видео по теме:

Определение и свойства

Основные свойства перевернутого треугольника:

1. Перевернутый треугольник имеет одну горизонтальную базу и несколько вертикальных линий.
2. Каждая вертикальная линия в перевернутом треугольнике короче предыдущей.
3. Перевернутый треугольник может иметь различное количество вертикальных линий, в зависимости от задачи или условия.
4. Перевернутый треугольник иногда называют пирамидой или обратным треугольником.
5. Перевернутый треугольник может быть использован в различных математических и геометрических задачах, а также в программировании и дизайне.

Перевернутый треугольник имеет интересные свойства и может быть использован для создания различных эффектов и узоров. Эта фигура применяется в различных областях, включая математику, физику, компьютерную графику и архитектуру.

Формулы и вычисления

Перевернутый треугольник в математике определяется следующим образом: если у нас есть треугольник, у которого вершина находится внизу, а основание сверху, то такой треугольник считается перевернутым.

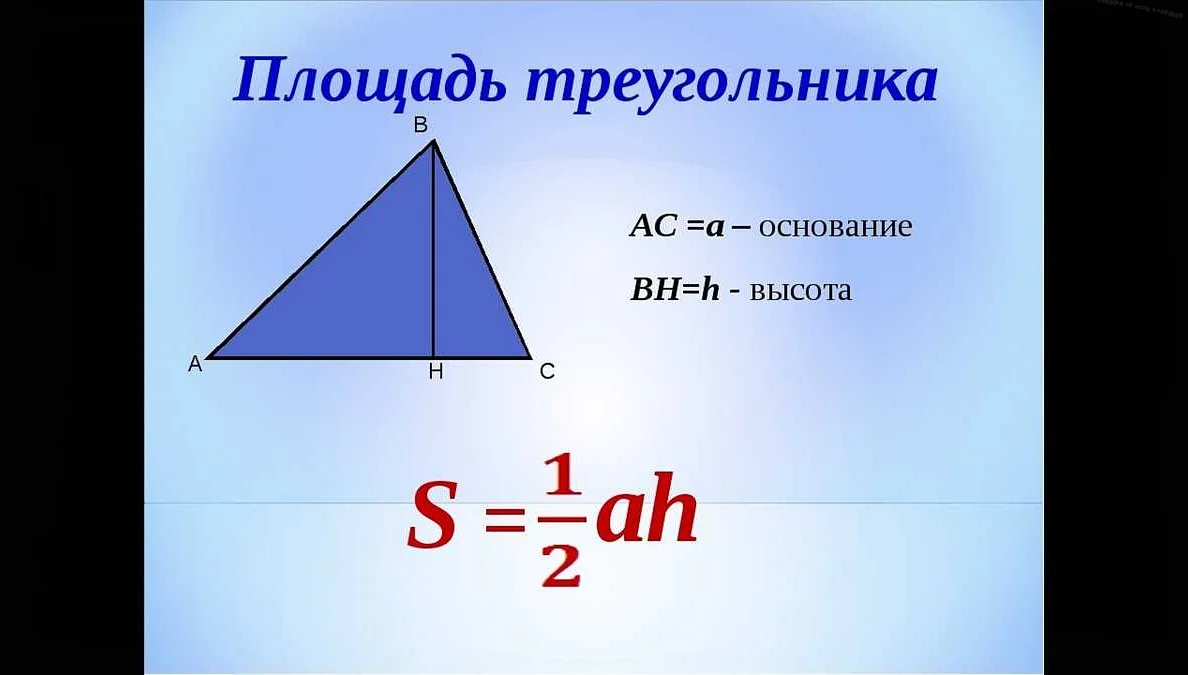
Чтобы вычислить площадь перевернутого треугольника, необходимо знать длину его основания и высоту. Формула для вычисления площади перевернутого треугольника выглядит следующим образом:

S = (b * h) / 2

где S — площадь перевернутого треугольника, b — длина основания, h — высота.

Также, для вычисления периметра перевернутого треугольника необходимо знать длины его сторон. Формула для вычисления периметра выглядит следующим образом:

P = a + b + c

где P — периметр перевернутого треугольника, a, b, c — длины сторон треугольника.

Формулы и вычисления позволяют определить геометрические характеристики перевернутого треугольника и использовать их для решения различных задач и проблем в математике и физике.

Вопрос-ответ:

Что такое перевернутый треугольник?

Перевернутый треугольник — это треугольник, у которого вершина находится внизу, а основание — вверху. В отличие от обычного треугольника, у которого основание находится внизу, а вершина — вверху.

Какое значение имеет перевернутый треугольник в математике?

Перевернутый треугольник имеет значение в различных областях математики, особенно в геометрии и алгебре. Он используется для решения различных задач и демонстрации различных свойств треугольников.

Какие свойства имеет перевернутый треугольник?

Перевернутый треугольник имеет те же свойства, что и обычный треугольник. Например, сумма углов в перевернутом треугольнике также равна 180 градусам. Он также может быть разделен на высоты, медианы и биссектрисы, и многие другие свойства, которые присущи треугольнику.

Как применяется перевернутый треугольник в геометрии?

Перевернутый треугольник может быть использован для решения задач по построению и доказательству свойств треугольников. Например, его можно использовать для нахождения углов треугольника, нахождения длин сторон треугольника, построения высот, медиан и биссектрис треугольника.

В каких областях математики применяется перевернутый треугольник, кроме геометрии?

Перевернутый треугольник также применяется в алгебре и арифметике. Например, его можно использовать для решения систем уравнений, нахождения значений переменных, а также для применения различных методов и приемов, связанных с алгеброй и арифметикой.

Зачем нужен перевернутый треугольник в математике?

Перевернутый треугольник является геометрической фигурой, которая имеет свое значение и применение в математике. Он используется, например, при решении задач на построение и измерение углов, рассмотрении свойств геометрических фигур и многих других математических задачах.

Как построить перевернутый треугольник?

Для построения перевернутого треугольника нужно провести основание треугольника, а затем провести биссектрису основания. Затем нужно провести линию, соединяющую вершину треугольника с серединой основания, и получится перевернутый треугольник.

Геометрическое представление

Геометрический контекст перевернутого треугольника имеет важное значение в различных областях математики и физики. Он широко используется в геометрии, при решении задач на построение и измерение фигур. Кроме того, перевернутый треугольник также применяется в тригонометрии, где его свойства используются для решения тригонометрических уравнений и вычисления углов.

Свойства перевернутого треугольника:

1. Углы: Углы перевернутого треугольника образуются противоположными сторонами. Они суммируются до 180 градусов.
2. Стороны: Стороны перевернутого треугольника соединяются в одной точке. Эта точка называется вершиной перевернутого треугольника.
3. Симметрия: Перевернутый треугольник обладает осью симметрии, которая проходит через вершину и середины сторон.

Геометрическое представление перевернутого треугольника помогает упростить его анализ и использование в различных математических проблемах. Знание основных свойств этой фигуры позволяет более эффективно решать задачи и добиваться точных результатов.

Применение в графике и дизайне

Перевернутый треугольник имеет широкое применение в графике и дизайне благодаря своей уникальной форме и символическому значению. Он может быть использован для создания различных эффектов и визуальных элементов, которые привлекают внимание и добавляют интерес к дизайну.

В графике и дизайне перевернутый треугольник может быть использован для создания следующих эффектов:

Силуэт Перевернутый треугольник может использоваться для создания силуэта объекта или фигуры. Он может быть использован для выделения контуров или формы объекта, добавляя графический интерес и эффектность к дизайну.	Динамика Перевернутый треугольник может быть использован для создания эффекта движения или динамики. Он может быть размещен таким образом, чтобы создать ощущение движения или направления, что делает дизайн более динамичным и энергичным.
Уравновешенность Перевернутый треугольник может быть использован для создания эффекта баланса или уравновешенности в дизайне. Он может быть размещен таким образом, чтобы создать визуальный баланс между различными элементами дизайна, что делает его более гармоничным и привлекательным для глаза.	Выделение Перевернутый треугольник может быть использован для выделения определенного элемента или информации в дизайне. Он может быть использован как стрелка, указывающая на важную часть дизайна и привлекающая внимание пользователя.

В целом, перевернутый треугольник является мощным графическим элементом, который может быть использован для создания различных эффектов и добавления интереса к дизайну. Его символическое значение, форма и геометрическое свойство делают его универсальным элементом, который может быть применен во многих различных контекстах и стилях дизайна.

Применение в программировании

Перевернутый треугольник также имеет широкое применение в программировании. Он используется для решения различных задач, таких как вывод графических элементов, генерация шаблонов и многое другое.

В программировании перевернутый треугольник можно вывести с помощью циклов. Например, используя циклы for или while, можно легко создать перевернутый треугольник из звездочек или любого другого символа.

Применение перевернутого треугольника в программировании может быть разнообразным. Например, он может использоваться для создания пирамиды или шаблона для вывода информации в виде заголовков или списков.

Также перевернутый треугольник может быть использован для создания графических элементов, таких как стрелки или декоративные украшения. Он может быть адаптирован для разных платформ и технологий, включая веб-разработку, мобильное приложение и настольное программное обеспечение.

Пример кода на языке Python:

for i in range(5, 0, -1): print(‘*’ * i)

Этот простой пример кода на языке Python демонстрирует, как можно создать перевернутый треугольник из звездочек. Вывод этого кода будет выглядеть следующим образом:

*****
****
***
**
*

Таким образом, применение перевернутого треугольника в программировании может быть очень полезным и разнообразным. Он используется для решения различных задач и может быть адаптирован для разных платформ и технологий.

Связь с другими фигурами

Перевернутый треугольник, также известный как угол с дополнением 180 градусов, имеет связь с другими геометрическими фигурами:

Прямоугольник: Перевернутый треугольник может быть вписан в прямоугольник, если основание треугольника совпадает с одной из сторон прямоугольника.

Квадрат: Если перевернутый треугольник имеет все стороны одинаковой длины, он может быть вписан в квадрат.

Параллелограмм: Перевернутый треугольник может быть вписан в параллелограмм, если его две стороны параллельны двум сторонам параллелограмма.

Трапеция: Если одна из сторон перевернутого треугольника параллельна одной из сторон трапеции, он может быть вписан в трапецию.

Окружность: Если перевернутый треугольник имеет все стороны одинаковой длины и центр окружности находится на одной из его сторон, он может быть вписан в окружность.

Эти связи с другими фигурами позволяют использовать перевернутые треугольники для решения различных геометрических задач и построений.

Значение в математических моделях

В геометрии перевернутый треугольник является основным строительным блоком для построения различных фигур. Он может быть использован для построения параллелограмма, ромба, трапеции и других геометрических фигур.

Также перевернутый треугольник имеет значение в алгебре и тригонометрии. В алгебре он может быть использован для решения уравнений и систем уравнений. В тригонометрии перевернутый треугольник помогает определять углы и стороны треугольника с помощью тригонометрических функций.

В математических моделях перевернутый треугольник может также использоваться для представления данных и отображения информации. Например, в графических моделях перевернутый треугольник может быть использован для обозначения направления или отрицательных значений.

Таким образом, перевернутый треугольник имеет значительное значение в математических моделях и может быть использован в различных областях науки и техники.

Примеры использования

Перевернутый треугольник в математике имеет несколько применений:

1. Геометрия:

Перевернутые треугольники могут быть использованы для решения геометрических задач, таких как нахождение площади фигуры или определение ее координат.

2. Графика:

Перевернутые треугольники часто используются в графических приложениях и программировании для создания различных форм и фигур.

3. Логика:

Перевернутые треугольники могут быть использованы в логических задачах, таких как составление таблиц истинности или нахождение логических связей между различными условиями.

4. Образование:

Перевернутые треугольники могут быть использованы в учебных материалах, связанных с обучением геометрии, графики или логики.

Это лишь некоторые примеры использования перевернутого треугольника в математике. Его значимость и применение зависят от конкретной задачи и области применения.