Площадь треугольника 3 класс математика как найти
Содержимое
- 1 Площадь треугольника 3 класс математика как найти
- 1.1 Что такое площадь треугольника?
- 1.2 Как вычислить площадь треугольника?
- 1.3 Формула для вычисления площади треугольника
- 1.4 Как найти высоту треугольника?
- 1.5 Как найти основание треугольника?
- 1.6 Примеры вычисления площади треугольника
- 1.7 Вопрос-ответ:
- 1.7.0.1 Как найти площадь треугольника?
- 1.7.0.2 Какой формулой можно найти площадь треугольника?
- 1.7.0.3 Что такое основание и высота треугольника?
- 1.7.0.4 Как определить основание и высоту треугольника?
- 1.7.0.5 Есть ли другие способы нахождения площади треугольника?
- 1.7.0.6 Как найти площадь треугольника?
- 1.8 Упражнения для тренировки
- 1.9 Видео по теме:
Узнайте, как найти площадь треугольника в математике для третьеклассников. Методы и формулы для расчета площади треугольника с примерами и объяснениями.
Площадь треугольника — это одно из основных понятий, которое изучается в математике для 3 класса. Понимание, как найти площадь треугольника, поможет детям развить навыки геометрии и решать простые задачи.
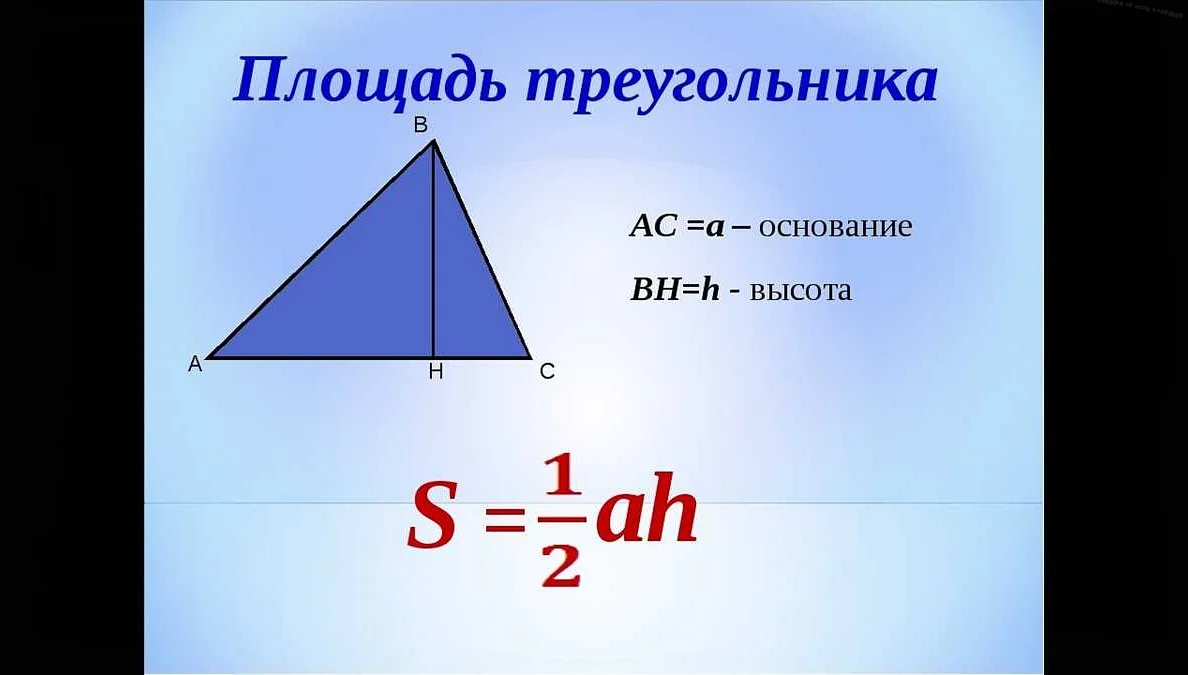
Для того чтобы найти площадь треугольника, нужно знать его основание и высоту. Основание — это одна из сторон треугольника, а высота — это отрезок, проведенный из вершины треугольника к его основанию и перпендикулярный ему.
Формула для нахождения площади треугольника выглядит следующим образом: площадь = (основание * высота) / 2. Для решения задачи достаточно взять известные значения основания и высоты, подставить их в формулу и выполнить несложные вычисления.
Пример: если основание треугольника равно 5 см, а высота равна 3 см, то площадь треугольника будет равна (5 * 3) / 2 = 7,5 квадратных сантиметра.
Учебник по математике для 3 класса обычно содержит разнообразные задачи, которые помогают детям применять полученные знания на практике. Поэтому очень важно понимать, как найти площадь треугольника и уметь применять соответствующие формулы для решения задач. По мере практики и опыта дети смогут легко находить площадь треугольника и использовать эту навык в своих будущих изучениях и повседневной жизни.
Что такое площадь треугольника?
Площадь треугольника можно вычислить, зная длины его сторон или длины одной стороны и высоту, опущенную на эту сторону. Для вычисления площади треугольника можно использовать формулу: площадь равна половине произведения длины основания на высоту, опущенную на это основание.
Например, если длина основания треугольника равна 6 единицам, а высота, опущенная на это основание, равна 4 единицам, то площадь треугольника будет равна половине произведения 6 и 4, то есть 12 квадратных единиц.
Знание площади треугольника позволяет нам измерять и сравнивать площади различных треугольников и использовать их в различных математических задачах и приложениях.
Как вычислить площадь треугольника?
Для вычисления площади треугольника нужно умножить длину основания на длину высоты, а затем разделить полученное значение на 2:
Площадь = (Основание * Высота) / 2
Например, если основание треугольника равно 5 см, а высота равна 8 см, то площадь можно найти следующим образом:
Площадь = (5 см * 8 см) / 2
Площадь = 40 см² / 2
Площадь = 20 см²
Таким образом, площадь треугольника равна 20 квадратным сантиметрам.
Формула для вычисления площади треугольника
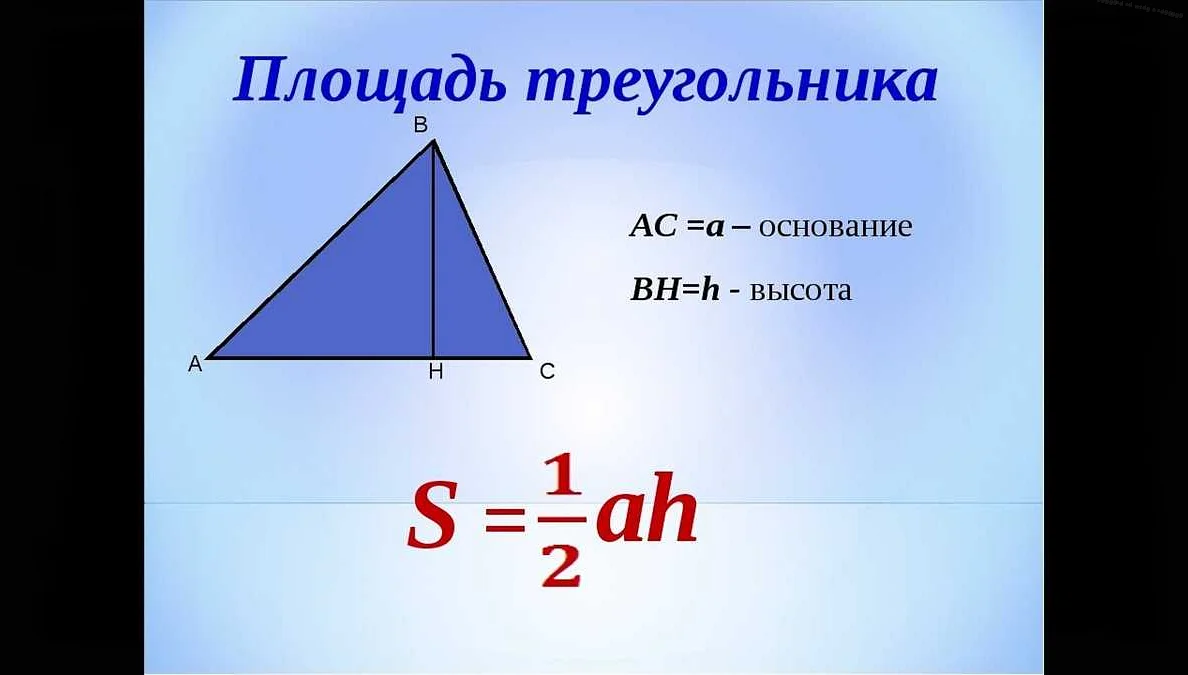
Формула для вычисления площади треугольника зависит от известных данных о треугольнике. Существует несколько способов расчета площади треугольника:
-
- Если известны длины двух сторон треугольника и угол между ними, площадь можно вычислить по формуле:
S = 0.5 * a * b * sin(α), где S — площадь треугольника, a и b — длины сторон треугольника, α — угол между этими сторонами.
-
- Если известны длины трех сторон треугольника, можно воспользоваться формулой Герона:
S = √(p * (p — a) * (p — b) * (p — c)), где S — площадь треугольника, p — полупериметр треугольника, вычисляемый по формуле p = (a + b + c) / 2, a, b и c — длины сторон треугольника.
-
- Если известны координаты вершин треугольника на плоскости, площадь можно вычислить по формуле:
S = 0.5 * |(x1 * (y2 — y3) + x2 * (y3 — y1) + x3 * (y1 — y2))|, где S — площадь треугольника, (x1, y1), (x2, y2) и (x3, y3) — координаты вершин треугольника.
Используя одну из этих формул, можно вычислить площадь треугольника на основе известных данных о нем.
Как найти высоту треугольника?
Высота = (2 * Площадь треугольника) / (длина основания треугольника)
Для нахождения высоты треугольника, необходимо знать длину основания треугольника и его площадь. Площадь треугольника можно найти, используя различные методы, например, формулу Герона или формулу площади прямоугольного треугольника. После нахождения площади треугольника, делим ее на длину основания, умножаем на 2 и получаем высоту треугольника.
Например, если длина основания треугольника равна 10 см, а площадь треугольника равна 30 квадратных см, то высота треугольника будет равна:
Высота = (2 * 30) / 10 = 6 см
Таким образом, высота треугольника равна 6 см.
Высота треугольника является важной характеристикой, которая помогает нам решать различные задачи в геометрии или других областях математики.
Как найти основание треугольника?
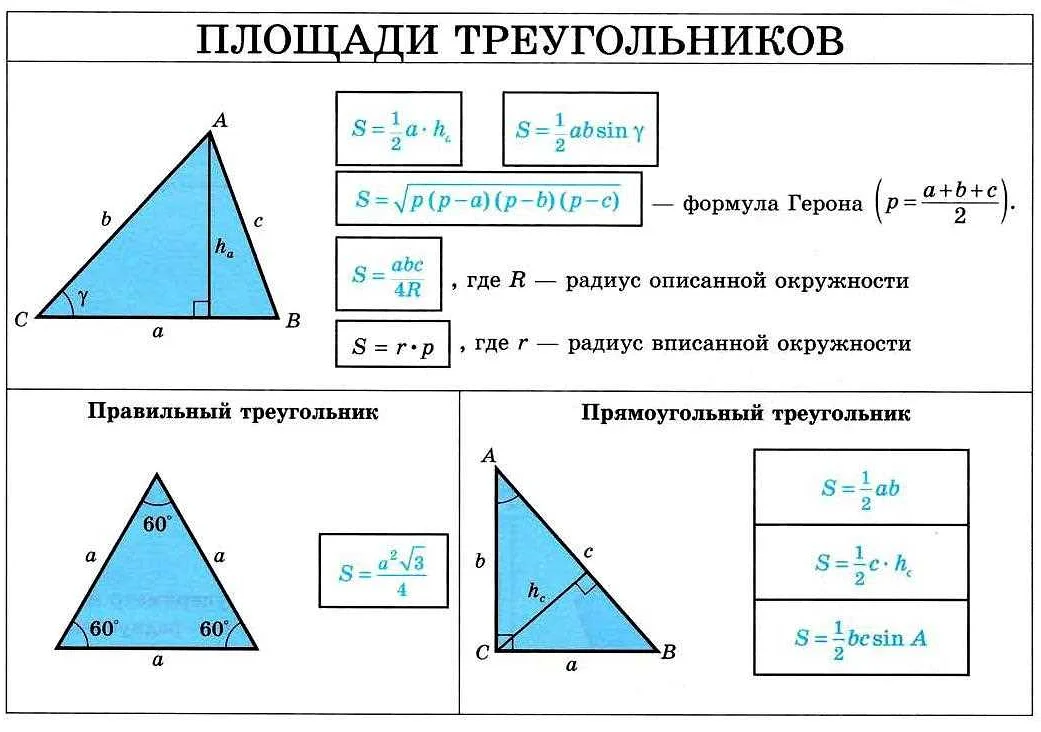
Чтобы найти основание треугольника, необходимо знать другие стороны и углы треугольника. Возможные способы определения основания треугольника:
- Если треугольник прямоугольный, то основание — это сторона, на которой лежит прямой угол.
- Если треугольник равносторонний, то все его стороны равны, поэтому можно выбрать любую из них в качестве основания.
- Если треугольник равнобедренный, то основание — это сторона, противолежащая равным углам.
- Если треугольник общего вида, то основание можно выбрать произвольно. В этом случае для вычисления площади треугольника потребуется дополнительная информация, например, высота или другие стороны и углы треугольника.
Обратите внимание, что основание треугольника может быть любой из его сторон в зависимости от его свойств. При решении задач на вычисление площади треугольника важно правильно определить основание для получения правильного результата.
Примеры вычисления площади треугольника
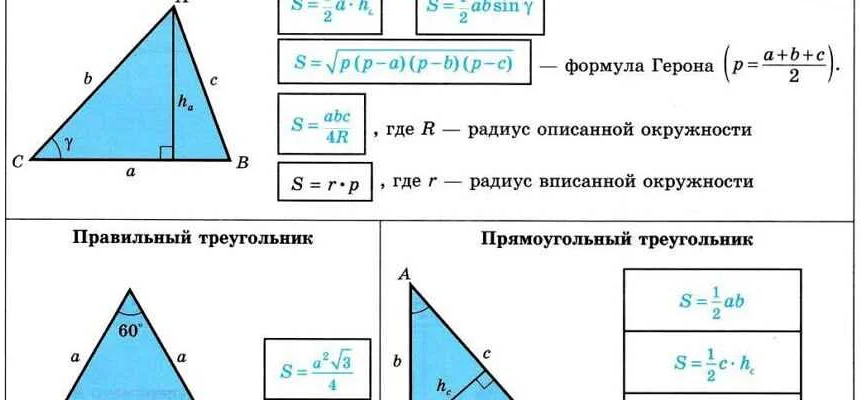
Для вычисления площади треугольника с помощью формулы необходимо знать длину основания и высоту. Рассмотрим несколько примеров вычисления площади треугольника.
-
- Пример 1:
Дан треугольник с основанием длиной 5 см и высотой 3 см. Для вычисления площади треугольника применим формулу: площадь = (основание * высота) / 2.
Подставляем значения в формулу: площадь = (5 * 3) / 2 = 7.5 см².
-
- Пример 2:
Дан треугольник с основанием длиной 8 см и высотой 6 см. Применяем формулу: площадь = (основание * высота) / 2.
Подставляем значения в формулу: площадь = (8 * 6) / 2 = 24 см².
-
- Пример 3:
Дан треугольник с основанием длиной 12 см и высотой 4 см. Применяем формулу: площадь = (основание * высота) / 2.
Подставляем значения в формулу: площадь = (12 * 4) / 2 = 24 см².
Таким образом, площадь треугольника может быть вычислена, зная длину основания и высоту. Формула для вычисления площади треугольника: площадь = (основание * высота) / 2.
Вопрос-ответ:
Как найти площадь треугольника?
Площадь треугольника можно найти, умножив половину основания на высоту.
Какой формулой можно найти площадь треугольника?
Формулой для нахождения площади треугольника является: площадь = (основание * высоту) / 2.
Что такое основание и высота треугольника?
Основание треугольника — это любая его сторона, на которую опирается высота. Высота треугольника — это отрезок, проведенный из вершины треугольника к основанию, под прямым углом.
Как определить основание и высоту треугольника?
Основание треугольника можно определить, выбирая любую его сторону. Высоту треугольника можно построить, проводя отрезок из вершины треугольника к основанию под прямым углом.
Есть ли другие способы нахождения площади треугольника?
Да, существуют и другие способы нахождения площади треугольника, например, с помощью формулы Герона или используя площадь треугольника как половину площади прямоугольника, в который треугольник вписан.
Как найти площадь треугольника?
Для нахождения площади треугольника нужно использовать следующую формулу: Площадь = (основание * высота) / 2. Основание треугольника – это одна из его сторон, а высота – перпендикуляр, опущенный из вершины треугольника на основание.
Упражнения для тренировки
Упражнение 1:
Найдите площадь треугольника, если его основание равно 5 см, а высота – 4 см.
Упражнение 2:
Найдите площадь треугольника, если длина основания равна 8 см, а высота – 6 см.
Упражнение 3:
Найдите площадь треугольника, если длина основания равна 10 см, а высота – 3 см.
Упражнение 4:
Найдите площадь треугольника, если длина основания равна 7 см, а высота – 9 см.
Упражнение 5:
Найдите площадь треугольника, если длина основания равна 12 см, а высота – 2 см.
Упражнение 6:
Найдите площадь треугольника, если длина основания равна 6 см, а высота – 10 см.
Упражнение 7:
Найдите площадь треугольника, если длина основания равна 9 см, а высота – 7 см.
Упражнение 8:
Найдите площадь треугольника, если длина основания равна 3 см, а высота – 5 см.
Упражнение 9:
Найдите площадь треугольника, если длина основания равна 11 см, а высота – 1 см.
Упражнение 10:
Найдите площадь треугольника, если длина основания равна 2 см, а высота – 8 см.



Отличная статья! Всегда интересно узнать что-то новое о математике. Нашел очень полезную информацию о нахождении площади треугольника. Всегда думал, что это сложно, но оказывается, есть простая формула. Теперь я знаю, что нужно умножить длину основания на высоту и поделить результат на 2. Также узнал о понятии «высота» треугольника, которая является перпендикулярной линией, проведенной из вершины треугольника к его основанию. Теперь мне кажется, что площадь треугольника можно легко найти, просто зная длину его основания и высоту. Спасибо за информацию! Я точно буду использовать это знание в будущем.
Спасибо за полезную статью о нахождении площади треугольника в математике для третьего класса! Я всегда задумывалась, как это делается, и ваше объяснение было очень понятным и простым. Мне понравилось, как вы использовали формулу «полупериметр треугольника умножить на радикал из разности полупериметра и каждого из его сторон». Это поможет детям запомнить формулу и легко применять ее на практике. Мне также понравилось, что вы привели примеры с конкретными числами, чтобы помочь нам лучше понять, как применять формулу. Это делает процесс еще более наглядным и понятным. Я уверена, что дети будут рады узнать о таком простом и эффективном способе нахождения площади треугольника. В целом, ваша статья была очень информативной и полезной. Я обязательно поделюсь ею с моими друзьями, у которых есть дети третьего класса. Спасибо за отличную работу и за то, что помогаете нам развивать наши математические навыки!
Спасибо за полезную статью! Моя дочь учится в третьем классе, и я всегда стараюсь поддерживать ее интерес к математике. Рад, что вы рассказали о том, как найти площадь треугольника, ведь это основная тема в нашей программе. Я уверен, что эта информация будет полезной и для других родителей и детей. Ваш подход к объяснению материала очень понятный и доступный. Мне нравится, что вы пошагово разбираете каждый этап решения задачи. Теперь, благодаря вашим объяснениям, моя дочь сможет легко найти площадь треугольника, зная длины его сторон. Я также хотел бы отметить, что ваше использование наглядных примеров и иллюстраций помогает визуализировать материал и делает его более интересным для детей. Моя дочь всегда больше впечатлена, когда математика представлена в игровой и занимательной форме. Спасибо, что делитесь своими знаниями и помогаете нам, родителям, поддерживать интерес детей к науке. Я буду следить за вашими новыми статьями и рекомендовать их другим родителям. Продолжайте в том же духе!
Отличная статья! Я всегда был заинтересован в математике, и нахождение площади треугольника — один из тех навыков, которые всегда пригодятся в жизни. Это так важно знать, особенно когда дело касается ремесленных работ или строительства. Мне понравилось, как автор дал нам простой и понятный способ нахождения площади треугольника. Я давно знал формулу половины произведения основания и высоты, но вам удалось объяснить это так, что даже третьекласснику будет понятно. Но самое интересное — это то, что вы показали нам примеры и даже дали упражнение для тренировки. Мне нравится, когда статьи предлагают не только теорию, но и практическое применение. Это помогает закрепить знания и дает возможность тренироваться. Конечно, я понимаю, что это только начало и что с годами мы будем изучать все более сложные методы нахождения площади треугольника, но ваша статья дает нам прекрасный стартовый материал. Я уверен, что третьеклассники смогут успешно освоить эти навыки. Спасибо за полезную информацию! Я буду рекомендовать эту статью своим друзьям и знакомым, которые также интересуются математикой.