Перевернутый вопросительный знак что означает в математике
Содержимое
- 1 Перевернутый вопросительный знак что означает в математике
- 1.1 Что означает перевернутый вопросительный знак в математике?
- 1.2 Видео по теме:
- 1.3 История и происхождение перевернутого вопросительного знака
- 1.4 Математические операции с использованием перевернутого вопросительного знака
- 1.5 Вопрос-ответ:
- 1.5.0.1 Каким образом используется перевернутый вопросительный знак в математике?
- 1.5.0.2 Какая функция кодируется при помощи перевернутого вопросительного знака?
- 1.5.0.3 Чему равен факториал числа, обозначаемый перевернутым вопросительным знаком?
- 1.5.0.4 В каких областях математики используется перевернутый вопросительный знак?
- 1.5.0.5 Как правильно читать перевернутый вопросительный знак?
- 1.6 Перевернутый вопросительный знак в уравнениях и формулах
- 1.7 Применение перевернутого вопросительного знака в логических выражениях
- 1.8 Аналогии и аналогичные символы в других областях науки и математики
- 1.9 Влияние перевернутого вопросительного знака на понимание и интерпретацию математических выражений
- 1.10 Как использовать перевернутый вопросительный знак в учебных материалах и преподавании математики
- 1.11 Популярные вопросы и сомнения об использовании перевернутого вопросительного знака в математике
Перевернутый вопросительный знак в математике используется для обозначения неопределенностей или возможных решений. Узнайте, как он применяется и что означает в различных математических контекстах.
Перевернутый вопросительный знак — это математический символ, обозначающий факториал числа. Он представляет собой восклицательный знак, повернутый вниз головой. В математике факториал числа N, обозначаемый как N!, равен произведению всех натуральных чисел от 1 до N.
Использование перевернутого вопросительного знака в математике имеет свои особенности. Например, факториал 0 равен 1: 0! = 1. Это правило следует из определения факториала и является одним из основных свойств этого математического оператора.
Пример использования:
5! = 5 * 4 * 3 * 2 * 1 = 120
3! = 3 * 2 * 1 = 6
1! = 1
Перевернутый вопросительный знак широко используется в комбинаторике и теории вероятностей для вычисления количества перестановок, сочетаний и размещений. Он также применяется в различных задачах теории чисел, математической статистике и других областях математики.
Изучение и понимание значения перевернутого вопросительного знака в математике помогает студентам и исследователям лучше понимать и решать сложные задачи, связанные с комбинаторикой и вероятностными расчетами.
Что означает перевернутый вопросительный знак в математике?
Перевернутый вопросительный знак используется в математике для выражения обратных отношений, функций или операций. Например, вместо записи «x + 2 = 5», можно записать «5 = x + 2», где перевернутый вопросительный знак обозначает обратное равенство.
Перевернутый вопросительный знак также используется для обозначения обратной функции. Например, если f(x) = y, то обратная функция обозначается как f-1(y) = x, где перевернутый вопросительный знак указывает на обратное отображение.
Обычно перевернутый вопросительный знак используется в сочетании с другими математическими символами, чтобы выразить обратные отношения и операции. Это позволяет более точно и компактно записывать математические выражения.
Важно помнить, что перевернутый вопросительный знак не является стандартным символом в обычном русском или английском языке, и его использование ограничено математическим контекстом.
Видео по теме:
История и происхождение перевернутого вопросительного знака
Происхождение этого знака не до конца ясно, однако существует несколько версий его истории.
Одна из версий гласит, что перевернутый вопросительный знак появился в Испании в конце XVI века. В то время испанский язык имел обыкновение ставить перед вопросительным предложением знак вопроса, состоящий из двух точек, похожих на восклицательный знак, но с обратной ориентацией. Со временем эти две точки объединились в один знак, который и стал использоваться как перевернутый вопросительный знак.
Другая версия связывает появление перевернутого вопросительного знака с латинскими монашескими рукописями. В этих рукописях иногда применялась аббревиатура Qo, которая означала латинское слово «quaestio» (вопрос). В течение времени эта аббревиатура развилась в знак вопроса, имеющий форму перевернутого вопросительного знака.
В настоящее время перевернутый вопросительный знак используется только в испанском языке, в то время как в других языках применяется обычный знак вопроса (?). Он является неотъемлемой частью испанской пунктуации и языковых правил и помогает сделать понимание вопросительных предложений более ясным.
Математические операции с использованием перевернутого вопросительного знака

Перевернутый вопросительный знак, который выглядит как обычный вопросительный знак, но перевернутый вверх ногами (¡), используется в математике для обозначения некоторых операций и свойств.
Вот несколько примеров:
- Умножение на ноль: ¡0 = 0. Это свойство позволяет упростить выражения и сделать операции с нулем более удобными.
- Деление на ноль: ¡a/0 = ∞. Здесь a — любое число, а ∞ обозначает бесконечность. Это свойство указывает на то, что деление на ноль не имеет определенного значения.
- Вычитание из нуля: ¡0 — a = -a. Это свойство позволяет упростить выражения и сделать операции с нулем более удобными.
- Извлечение квадратного корня: ¡a^2 = |a|. Здесь a — любое число, а |a| обозначает модуль числа a. Это свойство указывает на то, что при извлечении квадратного корня всегда получается положительное число.
Перевернутый вопросительный знак может также использоваться в других математических операциях и свойствах, но эти примеры демонстрируют основные его применения.
Вопрос-ответ:
Каким образом используется перевернутый вопросительный знак в математике?
Перевернутый вопросительный знак в математике используется для обозначения факториала числа.
Какая функция кодируется при помощи перевернутого вопросительного знака?
Перевернутый вопросительный знак используется для обозначения гамма-функции.
Чему равен факториал числа, обозначаемый перевернутым вопросительным знаком?
Факториал числа, обозначаемый перевернутым вопросительным знаком, равен произведению всех положительных целых чисел от 1 до этого числа.
В каких областях математики используется перевернутый вопросительный знак?
Перевернутый вопросительный знак используется в комбинаторике, теории вероятности и теории чисел.
Как правильно читать перевернутый вопросительный знак?
Перевернутый вопросительный знак читается как «факториал» или «гамма».
Перевернутый вопросительный знак в уравнениях и формулах
Когда перевернутый вопросительный знак появляется в уравнении, это означает, что нам необходимо найти значение этой переменной. Мы можем использовать алгебраические методы, чтобы решить уравнение и найти неизвестное значение. Например, в уравнении 2x + 5 = 15, перевернутый вопросительный знак обозначает переменную x, которую мы должны найти. Решив уравнение, мы можем найти, что x = 5.
Перевернутый вопросительный знак также может использоваться в формулах для обозначения переменных. Например, в формуле площади прямоугольника S = ab, где перевернутый вопросительный знак обозначает переменные a и b – длину и ширину прямоугольника. Мы можем подставить известные значения длины и ширины, чтобы найти площадь прямоугольника.
ПримерУравнение/ФормулаРешение/Значение
| Прямоугольник | S = ab | S = 5 * 8 = 40 |
| Уравнение | 2x + 5 = 15 | x = 5 |
Таким образом, перевернутый вопросительный знак играет важную роль в математике, помогая нам найти неизвестные значения в уравнениях и формулах. Он позволяет нам решать задачи и работать с переменными, которые мы должны найти или определить для достижения нужного результата.
Применение перевернутого вопросительного знака в логических выражениях
Перевернутый вопросительный знак (?, иногда также называемый «неопределенностью») широко используется в математике для обозначения логической неопределенности или неизвестности. Он может быть включен в логическое выражение в качестве переменной, значение которой неизвестно или может принимать различные значения.
Перевернутый вопросительный знак часто используется в условных выражениях, где он указывает на возможность наличия или отсутствия определенного значения. Например, в выражении «x > 5 ? true : false» перевернутый вопросительный знак указывает на то, что результатом выражения будет true, если значение переменной x больше 5, и false в противном случае.
В логических операциях перевернутый вопросительный знак может использоваться для обозначения отрицания. Например, если у нас есть выражение «!(x > 5)», оно будет истинным, если значение переменной x не больше 5.
Перевернутый вопросительный знак также может быть использован в условных операторах для обработки неопределенных или исключительных ситуаций. Например, в языке программирования Java оператор «try ? catch» используется для обработки исключений. Он указывает на то, что код в блоке «try» может вызвать исключение, и его обработка будет осуществляться в блоке «catch».
Аналогии и аналогичные символы в других областях науки и математики
Например, в логике и философии существуют символы, которые выражают понятие отрицания или противоположности. Один из таких символов — знак отрицания или знак противоположности (~). Он используется для выражения отрицания утверждения или понятия. В математике этот символ может быть использован для обозначения отрицания логического выражения, например «не A».
В физике также существуют символы, которые имеют аналогию с перевернутым вопросительным знаком. Например, символы, обозначающие векторы или направления. Один из таких символов — стрелка или векторная стрелка (→). Она используется для обозначения направления движения или силы в физических явлениях. В математике этот символ может быть использован для обозначения вектора или направления в пространстве.
Также в математике есть другие символы, которые могут иметь аналогию с перевернутым вопросительным знаком. Например, символы, обозначающие отношение или эквивалентность. Один из таких символов — знак равенства (=). Он используется для выражения равенства двух значений или объектов. В математике этот символ может быть использован для обозначения равенства уравнений или выражений.
Таким образом, хотя перевернутый вопросительный знак является характерным символом в математике, аналогии и аналогичные символы можно найти и в других областях науки и математики. Они используются для выражения различных понятий и отношений и имеют свою специфическую символику.
Влияние перевернутого вопросительного знака на понимание и интерпретацию математических выражений

Использование перевернутого вопросительного знака может существенно влиять на понимание и интерпретацию математических выражений. Он позволяет компактно записывать и вычислять факториалы больших чисел, что упрощает решение задач и проведение вычислений.
Кроме того, перевернутый вопросительный знак может использоваться в комбинаторике для обозначения количества возможных перестановок или сочетаний элементов множества. В этом случае он помогает уточнить смысл и задать точное значение, которое требуется вычислить или определить.
Однако, использование перевернутого вопросительного знака требует определенных знаний и навыков, особенно при работе с большими числами или сложными выражениями. Неправильное понимание или неверное использование может привести к ошибкам и искажению результата.
Поэтому, важно учитывать контекст и правильно интерпретировать перевернутый вопросительный знак при чтении математических выражений. Это поможет избежать ошибок и обеспечить точность и корректность проводимых вычислений.
Как использовать перевернутый вопросительный знак в учебных материалах и преподавании математики
Для использования перевернутого вопросительного знака в учебных материалах и преподавании математики следует придерживаться определенных правил:
- Правильно расставлять знаки препинания и пробелы. Перевернутый вопросительный знак ставится после числа без пробела, например: 5!
- Ясно объяснять значение перевернутого вопросительного знака. Необходимо понимать, что символ 5! означает факториал числа 5, и включить это объяснение в учебный материал или урок.
- Приводить примеры использования перевернутого вопросительного знака. Показать, как вычислять факториалы различных чисел и использовать перевернутый вопросительный знак в различных математических задачах.
- Подчеркнуть важность правильного использования перевернутого вопросительного знака. Объяснить, что неправильное использование этого символа может привести к неверным результатам и непониманию математических концепций.
В образовательных материалах и при преподавании математики использование перевернутого вопросительного знака помогает студентам лучше понять и запомнить концепцию факториала числа. Кроме того, это символ также позволяет углубиться в изучение комбинаторики и решать различные задачи, связанные с перестановками и сочетаниями.
Популярные вопросы и сомнения об использовании перевернутого вопросительного знака в математике
Вопросительный знак в математике обычно используется для обозначения вопросов или неизвестных значений. Однако, иногда встречается использование перевернутого вопросительного знака, что может вызывать сомнения и вопросы у студентов. В этом разделе мы рассмотрим некоторые популярные вопросы и сомнения об использовании перевернутого вопросительного знака в математике.
-
- Зачем нужен перевернутый вопросительный знак в математике?
Перевернутый вопросительный знак в математике используется для обозначения факториала. Факториал числа обозначается символом «!», и означает произведение всех положительных целых чисел от 1 до данного числа. Например, факториал числа 5 обозначается как 5! и равен 5 × 4 × 3 × 2 × 1 = 120.
-
- Как правильно читать перевернутый вопросительный знак?
Перевернутый вопросительный знак читается как «факториал». Например, 5! читается как «пять факториал» или «факториал пять».
-
- Как вычислить факториал числа?
Для вычисления факториала числа нужно умножить все положительные целые числа от 1 до данного числа. Например, чтобы вычислить 5!, нужно умножить 1 × 2 × 3 × 4 × 5 = 120.
-
- Какие ограничения есть на использование перевернутого вопросительного знака?
Перевернутый вопросительный знак может использоваться только для неотрицательных целых чисел. Например, факториал отрицательного числа или дробного числа не определен.
-
- Какие свойства имеет факториал?
Некоторые основные свойства факториала включают:
-
- Факториал нуля равен единице: 0! = 1
- Факториал единицы также равен единице: 1! = 1
- Факториал любого числа n больше либо равен 1: n! ≥ 1
- Факториал числа n является произведением всех целых чисел от 1 до n: n! = 1 × 2 × 3 × … × n
Надеемся, что эта информация поможет вам лучше понять и использовать перевернутый вопросительный знак в математике.


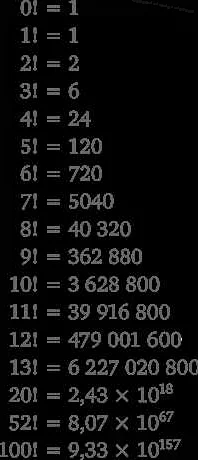
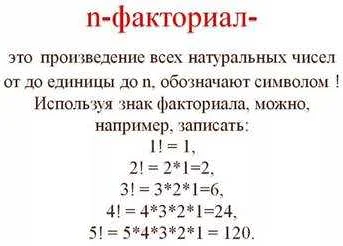
Интересно узнать о перевернутом вопросительном знаке в математике. Вообще, обычно вопросительный знак применяется для обозначения вопроса. Но как это связано с математикой? Честно говоря, даже не представляю. Может быть, это какой-то специальный знак, который используется для задания математических вопросов или для обозначения неизвестной величины? Хотелось бы узнать больше о его значении и использовании в математике. Возможно, это какой-то символ, который помогает решать сложные задачи или упрощает запись математических выражений. Хотелось бы разобраться в этом и понять, как использовать перевернутый вопросительный знак в своих математических расчетах. Жду с нетерпением дальнейшей информации на эту тему.
Эта статья действительно интересна и полезна. Я никогда не задавался вопросом о значении и использовании перевернутого вопросительного знака в математике. Оказывается, он имеет большое значение и используется для обозначения факториала числа. Это новая информация для меня, которую я с удовольствием узнал. Я считаю, что такие маленькие детали могут иметь огромное значение в математике, и это открывает для меня новые горизонты в изучении этой науки. Большое спасибо за информацию! Я обязательно буду продолжать изучать эту тему и делиться своими открытиями с другими.
Статья очень интересная и познавательная! Я никогда раньше не задумывался о том, что в математике есть перевёрнутый вопросительный знак. Это действительно удивительно, как один символ может иметь такое значение и использование. Я всегда считал, что вопросительный знак имеет только одну форму и функцию. Оказывается, в математике всё немного сложнее и интереснее. Использование перевёрнутого вопросительного знака, чтобы выразить факториал числа, это действительно гениально! Теперь я понимаю, что этот символ играет важную роль в математических выражениях и уравнениях. Большое спасибо автору за раскрытие этой темы! Теперь моё представление о математике стало немного шире и глубже.