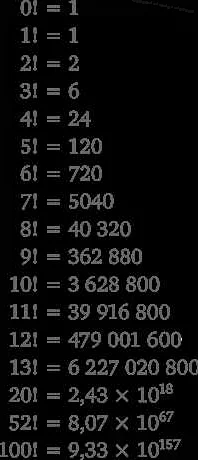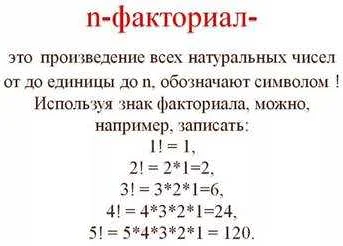Что значит восклицательный знак в математике после цифры

В математике восклицательный знак после цифры обозначает факториал числа. Узнайте, как работает факториал и как использовать его в математических выражениях.

В мире математики восклицательный знак имеет особое значение. Он используется для обозначения факториала, который является одной из важных операций в комбинаторике и анализе. Факториал числа обозначается символом «!» и представляет собой произведение всех положительных целых чисел, не больших данного числа.

Применение восклицательного знака в математике позволяет вычислять комбинаторные задачи, такие как количество перестановок, размещений и сочетаний элементов в заданном множестве. Например, факториал числа 5 равен 5! = 5 * 4 * 3 * 2 * 1 = 120.

Основным правилом использования восклицательного знака является его расположение после числа или переменной, для которой вычисляется факториал. Например, 5! или n! обозначают факториал числа 5 или переменной n соответственно.

Примеры:

1. Вычисление факториала числа:

4! = 4 * 3 * 2 * 1 = 24

2. Вычисление факториала переменной:

n! = n * (n-1) * (n-2) * … * 1

Восклицательный знак в математике имеет важное значение и позволяет упростить вычисления в комбинаторике и анализе. Знание основных правил использования и примеров поможет успешно решать задачи, связанные с факториалом чисел и переменных.

Восклицательный знак в факториале

В математике восклицательный знак (!) используется для обозначения факториала числа. Факториал числа n обозначается как n!, и представляет собой произведение всех натуральных чисел от 1 до n.

Например:

• Факториал числа 0 равен 1: 0! = 1
• Факториал числа 1 равен 1: 1! = 1
• Факториал числа 5 равен 120: 5! = 5 * 4 * 3 * 2 * 1 = 120
• Факториал числа 10 равен 3,628,800

Факториалы широко применяются в комбинаторике и анализе вероятностей для вычисления количества возможных перестановок и комбинаций.

Восклицательный знак в комбинаторике

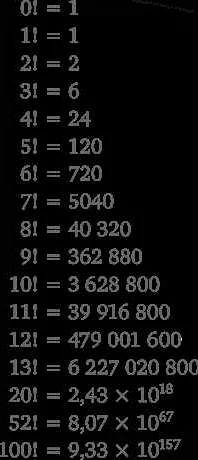
В комбинаторике восклицательный знак (!) используется для обозначения факториала числа. Факториал числа n обозначается как n! и равен произведению всех положительных целых чисел от 1 до n.

Например, факториал числа 5 будет выглядеть как 5! = 5 * 4 * 3 * 2 * 1 = 120.

Факториалы используются в комбинаторике для решения различных задач. Они помогают определить количество возможных комбинаций или перестановок элементов в некотором множестве.

Например, если у нас есть 5 различных предметов, то количество возможных перестановок этих предметов можно найти с помощью факториала: 5! = 120.

Кроме того, в комбинаторике также используется понятие двойного факториала. Двойной факториал числа n обозначается как n!! и равен произведению всех положительных целых чисел, не превышающих n, с четным индексом.

Например, двойной факториал числа 6 будет выглядеть как 6!! = 6 * 4 * 2 = 48.

Двойные факториалы также используются для решения задач комбинаторики, например, для определения количества возможных комбинаций при различных условиях.

Восклицательный знак в арифметике

Восклицательный знак (!) в арифметике используется для обозначения факториала числа. Факториал числа n обозначается n! и равен произведению всех натуральных чисел от 1 до n.

Например, факториал числа 5 (обозначается 5!) вычисляется следующим образом:

5! = 5 * 4 * 3 * 2 * 1 = 120

Таким образом, факториал числа 5 равен 120.

Важно отметить, что факториал определен только для натуральных чисел, т.е. положительных целых чисел. Факториал отрицательных чисел, дробей или чисел с плавающей запятой не определен.

Восклицательный знак в уравнениях

В математике восклицательный знак (факториал) используется для обозначения произведения всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 обозначается как 5! и равен произведению 5 * 4 * 3 * 2 * 1 = 120.

В уравнениях восклицательный знак может использоваться для обозначения факториала как одного из компонентов уравнения. Например, рассмотрим уравнение:

3! + x = 10

В данном уравнении восклицательный знак перед числом 3 обозначает факториал этого числа. Таким образом, уравнение можно прочитать как «факториал числа 3, плюс x, равно 10». Чтобы найти значение переменной x, необходимо решить это уравнение.

Другой пример:

2x + 4! = 24

В данном уравнении восклицательный знак перед числом 4 обозначает факториал числа 4. Уравнение можно прочитать как «2 умножить на x, плюс факториал числа 4, равно 24». Чтобы найти значение переменной x, необходимо решить это уравнение.

Таким образом, восклицательный знак может использоваться в уравнениях для обозначения факториала числа как одного из компонентов уравнения.

Восклицательный знак в математических операциях

В математике восклицательный знак (!) имеет специальное значение и обозначает факториал числа. Факториал числа представляет собой произведение всех натуральных чисел от 1 до этого числа включительно.

Факториал числа обозначается с помощью восклицательного знака перед числом. Например, факториал числа 5 записывается как 5!.

Пример вычисления факториала числа 5:

1. Умножаем все натуральные числа от 1 до 5:
   • 1 * 2 * 3 * 4 * 5 = 120
2. Таким образом, факториал числа 5 равен 120.

Восклицательный знак также можно использовать для обозначения воскресного оператора, который обозначает «не равно». Например, если a ≠ b, то это можно записать как a ≠ b.

В математических операциях восклицательный знак имеет строго определенное значение, которое следует учитывать при решении задач и вычислениях.

Восклицательный знак в статистике

Обозначение факториала числа N с помощью восклицательного знака выглядит следующим образом: N!. Например, факториал числа 5 обозначается как 5! и равен 5 * 4 * 3 * 2 * 1 = 120.

В статистике факториалы используются для решения различных задач, таких как вычисление числа сочетаний и перестановок, расчет вероятностей и многих других. Они также широко применяются в комбинаторике, теории вероятностей и математической статистике.

Например, факториалы используются для вычисления числа сочетаний, которое определяет количество способов выбрать K элементов из N элементов без учета порядка. Формула для вычисления числа сочетаний выглядит следующим образом: C(N, K) = N! / (K! * (N — K)!), где N — общее количество элементов, K — количество выбранных элементов.

Таким образом, восклицательный знак в статистике играет важную роль в вычислениях и анализе данных, помогая решать различные задачи и определять вероятности.

Восклицательный знак в математическом анализе

В математическом анализе восклицательный знак «!» используется для обозначения факториала числа. Факториал числа «n» обозначается как «n!» и представляет собой произведение всех положительных целых чисел от 1 до «n». Например, факториал числа 5 обозначается как «5!» и равен 5 * 4 * 3 * 2 * 1 = 120.

Восклицательный знак также может использоваться для обозначения восклицательной функции Гамма. Восклицательная функция Гамма является обобщением факториала на комплексную плоскость и определяется как интеграл от функции с переменной «t», возведенной в степень «z-1», умноженной на экспоненту и сами функции Гамма. Обозначается восклицательным знаком перед аргументом функции. Например, восклицательная функция Гамма от числа 5 обозначается как «5!» и равняется 4! = 24.

Использование восклицательного знака в математическом анализе позволяет удобно и компактно записывать произведение или интеграл от последовательности чисел или функций.

Восклицательный знак в теории вероятности

Восклицательный знак (!) в теории вероятности используется для обозначения факториала числа. Факториал числа n обозначается как n! и представляет собой произведение всех целых чисел от 1 до n.

Например, факториал числа 5 обозначается как 5! и вычисляется как 5 * 4 * 3 * 2 * 1 = 120.

Факториалы широко применяются в задачах комбинаторики и теории вероятности для вычисления количества возможных комбинаций и перестановок.

Факториалы также используются для определения вероятности событий в комбинаторных задачах. Например, вероятность получить определенную комбинацию из n элементов можно вычислить как отношение числа комбинаций с этой комбинацией к общему числу возможных комбинаций. Формула для вычисления такой вероятности может содержать восклицательные знаки.

Важно отметить, что факториал определяется только для положительных целых чисел. Факториал отрицательного числа, дробного числа или нуля не определен.

Использование восклицательного знака в теории вероятности позволяет более удобно вычислять комбинаторные задачи и определять вероятности различных событий.

Видео по теме:

Какое значение имеет восклицательный знак в математике?

Восклицательный знак в математике обычно используется для обозначения факториала числа. Например, 5! (читается «пять факториал») означает произведение всех натуральных чисел от 1 до 5.

Как правильно использовать восклицательный знак в математике?

Восклицательный знак ставится после числа, для которого нужно вычислить факториал. Например, 5! = 5 * 4 * 3 * 2 * 1 = 120. Также восклицательный знак можно использовать в выражениях для обозначения восклицания или удивления, но это уже не связано с математикой.

Можно ли использовать восклицательный знак для обозначения восклицания или удивления в математике?

Восклицательный знак может использоваться в выражениях для обозначения восклицания или удивления, однако это уже не связано с математикой. В математике восклицательный знак обычно используется только для обозначения факториала числа.