Математика что значит восклицательный знак
Содержимое
- 1 Математика что значит восклицательный знак
- 1.1 Восклицательный знак в математике: общая информация
- 1.2 Значение восклицательного знака в факториале
- 1.3 Применение восклицательного знака в комбинаторике
- 1.4 Восклицательный знак в теории вероятностей
- 1.5 Использование восклицательного знака в уравнениях и неравенствах
- 1.6 Восклицательный знак в математической статистике
- 1.7 Значение восклицательного знака в математических выражениях и функциях
- 1.8 Примеры использования восклицательного знака в математике
- 1.9 Видео по теме:
Восклицательный знак в математике обозначает факториал числа. Узнайте, что это такое и как он используется в вычислениях.
Восклицательный знак, часто называемый факториалом, является одной из важных математических операций. Он используется для обозначения произведения всех натуральных чисел от заданного числа до единицы. Например, факториал числа 5 обозначается как 5! и равен 5 * 4 * 3 * 2 * 1 = 120.
Основное правило использования восклицательного знака в математике состоит в том, что факториал может быть вычислен только для неотрицательных целых чисел. Натуральное число 0 имеет факториал равный 1, поскольку умножение на 1 не меняет значение числа. Не существует факториала отрицательного числа или дробного числа.
Восклицательный знак может быть использован в различных математических задачах и формулах. Например, он часто встречается в комбинаторике, где используется для вычисления количества перестановок или сочетаний элементов. Также он может быть использован для вычисления вероятностей в некоторых задачах теории вероятностей.
Пример использования факториала в математике: вычислить количество способов разместить 4 различных предмета на полке. Это можно сделать, вычислив факториал числа 4, то есть 4! = 4 * 3 * 2 * 1 = 24. Таким образом, существует 24 различных способа разместить 4 предмета на полке.
В заключение, восклицательный знак в математике является важным инструментом для вычисления произведения всех натуральных чисел от заданного числа до единицы. Он используется в различных математических задачах и формулах, и правильное использование этой операции позволяет получить точные и корректные результаты.
Восклицательный знак в математике: общая информация
Восклицательный знак в математике имеет особое значение и обозначает факториал числа. Факториал числа n обозначается символом n! и представляет собой произведение всех натуральных чисел от 1 до n.
Например, факториал числа 5 выглядит следующим образом: 5! = 5 * 4 * 3 * 2 * 1 = 120.
Факториал часто используется в комбинаторике, теории вероятностей и других областях математики. Он позволяет вычислять количество возможных комбинаций, перестановок и размещений элементов.
С помощью факториала можно решать задачи, связанные с вычислением вероятностей, нахождением количества возможных вариантов и другими задачами, требующими подсчета количества комбинаций.
Для вычисления факториала числа n можно использовать формулу:
n! = n * (n-1) * (n-2) * … * 2 * 1.
Факториал числа 0 определен равным 1, то есть 0! = 1.
Использование восклицательного знака в математике позволяет упростить вычисления и обозначить факториал числа. Это важный инструмент при решении различных математических задач и применяется во многих областях науки.
Значение восклицательного знака в факториале
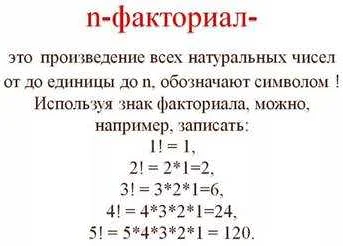
Например, факториал числа 4 обозначается как 4!, и равен произведению 4 * 3 * 2 * 1, то есть 24.
Факториал используется в различных областях математики, таких как комбинаторика, теория вероятностей и анализ алгоритмов.
Значение факториала может быть вычислено с помощью цикла или рекурсии. Например, в программировании вычисление факториала числа может быть реализовано следующим образом:
int factorial(int n) {
int result = 1;
for (int i = 1; i
Таким образом, восклицательный знак в факториале играет важную роль при вычислении значений факториала чисел и имеет практическое применение в различных областях математики и программирования.
Применение восклицательного знака в комбинаторике
В комбинаторике восклицательный знак используется для обозначения факториала числа. Факториал числа n обозначается как n! и представляет собой произведение всех натуральных чисел от 1 до n.
Применение восклицательного знака в комбинаторике позволяет решать задачи на перестановки, сочетания и размещения объектов.
Например, для вычисления числа перестановок из n элементов можно использовать формулу:
- П(n) = n!
где П(n) — число перестановок.
Также, для вычисления числа сочетаний из n элементов по k элементов можно использовать формулу:
- C(n, k) = n! / (k! * (n — k)!)
где C(n, k) — число сочетаний.
Использование восклицательного знака в комбинаторике позволяет упростить вычисления и получить точные результаты.
Восклицательный знак в теории вероятностей
Восклицательный знак также имеет свое значение в теории вероятностей. В этой области математики он используется для обозначения факториала числа.
Факториал числа — это умножение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 равен 5! = 5 × 4 × 3 × 2 × 1 = 120.
В теории вероятностей факториалы используются для определения количества возможных комбинаций или перестановок элементов в выборке или множестве.
Например, если у нас есть множество из 5 элементов, то количество возможных перестановок этих элементов можно вычислить с помощью факториала: 5! = 5 × 4 × 3 × 2 × 1 = 120.
Также восклицательный знак может использоваться для обозначения формулы Бернулли в теории вероятностей. Формула Бернулли позволяет вычислить вероятность наступления события в серии экспериментов с двумя возможными исходами (например, успехом или неудачей).
Использование восклицательного знака в теории вероятностей позволяет упростить вычисления и обозначить количество комбинаций или перестановок элементов в выборке или множестве.
Использование восклицательного знака в уравнениях и неравенствах

Однако, восклицательный знак также может использоваться в уравнениях и неравенствах для обозначения факториала переменной. Например, если у нас есть уравнение x! = 120, то это означает, что значение переменной x должно быть таким, чтобы факториал этого значения равнялся 120.
Восклицательный знак также может использоваться в неравенствах с факториалами переменных. Например, если у нас есть неравенство x! > 10, то это означает, что значение переменной x должно быть таким, чтобы факториал этого значения был больше 10.
Использование восклицательного знака в уравнениях и неравенствах может приводить к различным решениям, в зависимости от значения факториала и требуемого неравенства. Поэтому важно внимательно анализировать и решать подобные уравнения и неравенства.
Восклицательный знак в математической статистике

В математической статистике восклицательный знак используется для обозначения факториала числа. Факториал числа n обозначается как n! и представляет собой произведение всех положительных целых чисел от 1 до n.
Факториал часто используется в комбинаторике и вероятностных расчетах. Например, для определения числа способов размещения n различных элементов в последовательности из n мест, используется формула n!.
Также восклицательный знак может использоваться в формуле для вычисления числа сочетаний. Число сочетаний обозначается как C(n, k) и вычисляется по формуле:
C(n, k) = n! / (k!(n-k)!),
где n — общее число элементов, а k — количество элементов, которые нужно выбрать.
В математической статистике восклицательный знак играет важную роль при вычислении вероятностей, оценке параметров распределений и проверке статистических гипотез. Он позволяет учитывать комбинаторные аспекты задач и получать точные результаты.
Важно помнить, что факториал растет очень быстро с ростом числа и может привести к большим значениям. Поэтому при работе со значениями факториала необходимо быть осторожным и использовать численные методы или специализированные функции для его вычисления.
Значение восклицательного знака в математических выражениях и функциях

Восклицательный знак в математике имеет несколько различных значений в разных контекстах. В основном, он используется для обозначения факториала числа. Факториал числа $n$, обозначаемый как $n!$, представляет собой произведение всех положительных целых чисел от 1 до $n$. Например, $5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$.
Восклицательный знак также может использоваться в математических функциях. Например, в математическом анализе он используется для обозначения обобщенного факториала, который определяется через гамма-функцию. Гамма-функция, обозначаемая как $\Gamma(x)$, представляет собой расширение понятия факториала на комплексную плоскость. Например, если $x$ — положительное целое число, то $\Gamma(x) = (x-1)!$. Однако, гамма-функция определена и для значений $x$, не являющихся целыми числами.
В математических выражениях восклицательный знак может использоваться для обозначения отрицания. Например, если $x$ — истина, то $
eg x$ — ложь, и наоборот. В логике это называется отрицанием.
Кроме того, восклицательный знак может использоваться для обозначения абсолютной величины числа. Например, $|x|$ обозначает абсолютное значение числа $x$, то есть его расстояние до нуля на числовой оси. Например, $|-5| = 5$, а $|3| = 3$.
Таким образом, восклицательный знак в математике имеет несколько различных значений в разных контекстах. В основном, он используется для обозначения факториала числа, гамма-функции, отрицания и абсолютной величины числа.
Примеры использования восклицательного знака в математике
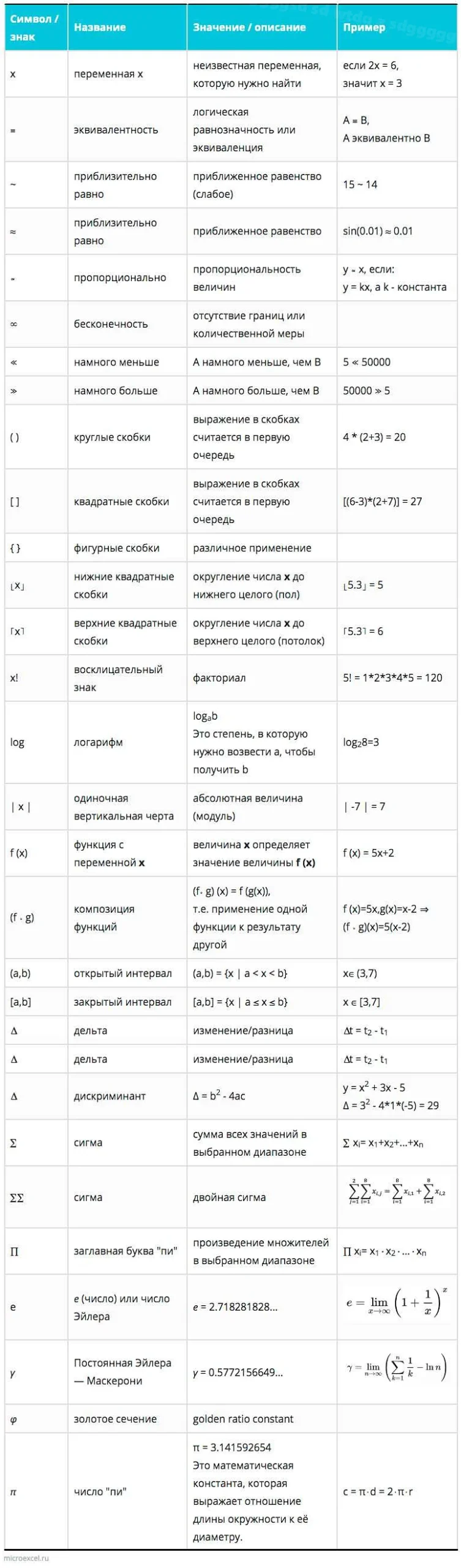
Например, факториал числа 5 обозначается как 5! и вычисляется как:
5! = 5 × 4 × 3 × 2 × 1 = 120
Также восклицательный знак может использоваться для обозначения отрицания в логических выражениях. Например, если у нас есть высказывание «a = 3», то отрицание этого высказывания будет записываться как «a ≠ 3» или «a != 3″.
Восклицательный знак также может использоваться для обозначения факториала вместе с переменными. Например, если у нас есть переменная n, то факториал этой переменной можно записать как n!. Например:
3! = 3 × 2 × 1 = 6
n! = n × (n-1) × (n-2) × … × 2 × 1
Таким образом, восклицательный знак в математике имеет несколько различных значений и используется для обозначения факториала чисел или переменных, а также для обозначения отрицания в логических выражениях.
Видео по теме:
Зачем нужен восклицательный знак в математике?
Восклицательный знак в математике обозначает факториал числа, т.е. произведение всех положительных целых чисел от 1 до данного числа. Например, 5! (читается как «пять факториал») равно 5 * 4 * 3 * 2 * 1 = 120. Таким образом, восклицательный знак позволяет выразить факториал числа.
Как вычислить факториал числа с помощью восклицательного знака?
Для вычисления факториала числа с помощью восклицательного знака нужно записать данное число и поставить после него восклицательный знак. Затем нужно последовательно умножать все числа от 1 до данного числа. Например, чтобы вычислить факториал числа 4, нужно записать 4! и выполнить операцию: 4 * 3 * 2 * 1 = 24. Таким образом, факториал числа можно вычислить с помощью восклицательного знака и последовательного умножения чисел.
Можно ли вычислить факториал десятичной дроби?
Факториал определен только для целых положительных чисел. Десятичные дроби, отрицательные числа и нуль не имеют факториала. Поэтому нельзя вычислить факториал десятичной дроби с помощью восклицательного знака. Восклицательный знак используется только для целых положительных чисел.

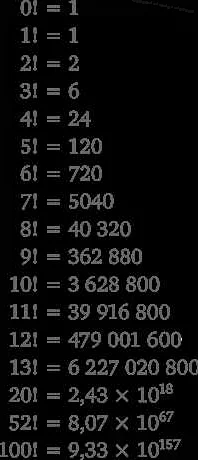


Очень интересная статья! Я всегда задавалась вопросом о значении восклицательного знака в математике. Теперь я наконец-то разобралась! Оказывается, восклицательный знак обозначает факториал числа. Это такая удивительная математическая операция, которая показывает, сколько раз можно умножить число на все предыдущие числа до единицы. Теперь мне понятно, почему факториалы используются в комбинаторике и статистике. Они помогают решать задачи, связанные с перестановками и сочетаниями объектов. Например, если нам нужно посчитать количество возможных комбинаций из 5 элементов, мы можем воспользоваться факториалом: 5!. Это равно 5 * 4 * 3 * 2 * 1 = 120. Также я узнала, что восклицательный знак может использоваться для обозначения восклицания в формулах. В этом случае он добавляется в конец выражения и показывает, что результат является существенным. Здорово, что теперь я знаю правила использования восклицательного знака в математике!