Что такое перевод в математике
Содержимое
Перевод в математике — это процесс изменения формулы, выражения или уравнения из одной системы обозначений в другую. Перевод может включать замену переменных, символов или операций, а также преобразование выражений с учетом математических правил. Умение переводить математические выражения из одной формы в другую является важным навыком в области математики и науки в целом.
Перевод — это одно из важнейших понятий в математике. Он позволяет нам связывать и анализировать различные объекты и явления, а также строить логические рассуждения и доказательства. Перевод может быть простым или сложным, зависит от конкретной задачи. В математике существует множество способов выполнить перевод, и каждый из них имеет свои особенности и применение.
Одной из основных задач перевода является нахождение соответствия между различными математическими объектами. Например, можно перевести числа в геометрические фигуры или функции в графики. Такой перевод позволяет нам визуализировать и анализировать сложные математические концепции, делая их более понятными и доступными.
Примером простого перевода может служить перевод чисел в слова. Например, число 123 может быть переведено как «сто двадцать три». Это позволяет нам описать числа с помощью слов и использовать их в различных контекстах, например, в текстовых задачах.
Сложный перевод в математике может включать в себя более сложные операции и преобразования. Например, в алгебре мы можем переводить уравнения в графики функций или наоборот, находить уравнения функций по их графикам. Это позволяет нам анализировать свойства функций, решать уравнения и находить решения задач в различных областях, включая физику, экономику и технику.
В данной статье мы рассмотрим различные способы перевода в математике и приведем примеры их применения в различных областях. Мы также рассмотрим особенности каждого из способов перевода и объясним, как выбрать наиболее подходящий способ для решения конкретных задач.
Что такое перевод в математике?
Цель перевода в математике часто заключается в упрощении выражений или решении уравнений. Путем применения определенных переходов и преобразований к исходным выражениям, математики могут добиться более простой или понятной формы, которая упрощает анализ или решение задачи.
Примеры перевода в математике включают раскрытие скобок, факторизацию, сокращение дробей, приведение подобных слагаемых и множителей, а также использование формул и свойств математических операций.
Перевод в математике является важным инструментом, который позволяет упростить и анализировать математические выражения и задачи. Он также позволяет математикам находить эквивалентные формы выражений и решать уравнения.
Видео по теме:
Определение понятия «перевод»

Переводы в математике широко используются для решения задач, доказательств теорем, упрощения выражений и выполнения других операций. Они могут включать в себя арифметические операции, преобразования алгебраических выражений, замену переменных, изменение масштаба и др. Переводы могут быть применены к различным типам математических объектов, таким как числа, функции, уравнения, графики и т.д.
Примерами переводов могут быть сокращение дробей, раскрытие скобок в алгебраическом выражении, факторизация полиномов, нахождение производной функции, решение уравнения и т.д. Каждый из этих переводов имеет свои правила и методы, которые определяются математической теорией и свойствами объектов, с которыми работает перевод.
Роль перевода в математике
Перевод в математике играет ключевую роль, поскольку позволяет устанавливать соответствие между математическими понятиями и языком, которым мы пользуемся для их описания. Это позволяет нам обмениваться информацией и идеями, а также договариваться о разных математических концепциях.
Перевод в математике может быть как межъязыковым, то есть переводом между различными языками, так и внутриязыковым, то есть переводом между математическими представлениями и символами. Например, когда мы переводим математическую формулу на английский язык, или когда мы переводим график функции в символьное представление.
Перевод в математике также играет важную роль в образовании и коммуникации. Он позволяет студентам исследовать и понимать математические концепции, а также обмениваться своими идеями и результатами с другими математиками.
Кроме того, перевод в математике помогает нам развивать абстрактное мышление и логическое мышление. Перевод математической задачи из словесного описания в формальное представление требует анализа и структурирования информации, а также применения логических законов и правил. Это способствует развитию наших мыслительных навыков и способности решать сложные задачи.
Таким образом, перевод является неотъемлемой частью математики и играет важную роль в образовании, исследованиях и коммуникации. Он помогает нам понимать и описывать математические концепции, а также развивает наши мыслительные навыки.
Вопрос-ответ:
Что такое перевод в математике?
Перевод в математике — это процесс, при котором одни математические объекты или явления преобразуются в другие с целью упрощения, анализа или решения задач.
Зачем нужен перевод в математике?
Перевод в математике позволяет упростить задачи и явления, разбивая их на более простые составляющие. Это помогает в анализе и понимании сложных математических объектов и явлений.
Какие примеры перевода в математике можно привести?
Примеры перевода в математике включают перевод текстовой задачи в алгебраическое уравнение, перевод геометрической фигуры в алгоритмическое описание, перевод словесного описания функции в ее математическую формулу и другие.
Какими методами можно осуществлять перевод в математике?
Перевод в математике может осуществляться различными методами, включая алгебраические преобразования, геометрические построения, использование математических символов и формул, а также применение специальных алгоритмов и арифметических операций.
Какие навыки помогут в осуществлении перевода в математике?
Для осуществления перевода в математике необходимы навыки анализа, логического мышления, умение работать с различными математическими представлениями, а также знание основных математических понятий и методов.
Основные виды перевода

Перевод словесных задач в алгебраический вид
Один из основных видов перевода – это перевод словесных задач в алгебраический вид. В этом случае, задача описывается словами, и ее необходимо перевести в язык алгебры, используя переменные и алгебраические операции. Такой перевод позволяет более удобно работать с задачей и найти ее решение с помощью алгебраических методов.
Перевод из одной системы счисления в другую
Другой важный вид перевода – это перевод чисел из одной системы счисления в другую. В математике существует несколько систем счисления, таких как десятичная, двоичная, восьмеричная и шестнадцатеричная. Перевод чисел из одной системы в другую позволяет представить число в удобной для обработки форме или сравнить числа, записанные в разных системах.
Перевод уравнений и неравенств
Также перевод может быть использован для преобразования уравнений и неравенств. При решении математических задач часто возникает необходимость перевести уравнение или неравенство из одной формы в другую, чтобы проще найти их решение или проанализировать свойства уравнения.
Перевод в математике имеет большое значение, так как позволяет удобно работать с математической информацией и решать задачи с использованием различных методов и подходов.
Преобразование формул в математике

Существует множество методов и правил для преобразования формул. Некоторые из них включают:
- Разложение скобок — позволяет раскрыть скобки в выражении, применяя правила распределительного закона.
- Факторизация — позволяет выделить общий множитель или привести выражение к каноническому виду.
- Сокращение дробей — позволяет упростить дробное выражение, сокращая числитель и знаменатель на их общие множители.
- Замена переменных — позволяет заменить переменные в выражении на новые, что может упростить вычисления или доказательства.
- Приведение подобных слагаемых — позволяет объединить слагаемые с одинаковыми переменными и степенями.
Преобразования формул могут быть использованы как в простых арифметических выражениях, так и в более сложных математических уравнениях. Они требуют внимательности и точности, чтобы сохранить эквивалентность исходной формулы.
Правильное применение преобразования формул может помочь найти решение задачи или доказать математическое утверждение. Оно является важным навыком для учащихся и специалистов в области математики и науки.
Перевод логических утверждений

Для перевода логических утверждений в математике используются различные символы и операторы. Один из наиболее распространенных способов перевода логических утверждений — использование таблиц истинности.
Таблица истинности представляет собой таблицу, в которой перечислены все возможные комбинации истинности для каждого из условий и выводов. Каждая комбинация истинности помечается как истинная (1) или ложная (0).
Пример перевода логического утверждения с помощью таблицы истинности:
УсловиеВывод
| Истина | Ложь |
| Ложь | Истина |
Таким образом, в данном примере логическое утверждение «Если условие истинно, то вывод ложен» можно записать как «Условие → Вывод».
В математике существуют различные способы перевода логических утверждений, включая обратное утверждение, контрапозицию, конъюнкцию, дизъюнкцию и т. д. Каждый из этих способов имеет свои правила и свойства, которые позволяют упростить и анализировать логические утверждения.
Перевод логических утверждений является важным инструментом в математике и помогает разрабатывать и проверять различные теории и утверждения. Правильное и точное перевод логических утверждений позволяет проводить логические рассуждения и доказательства, а также применять математические методы для решения различных задач.
Примеры перевода в математике
-
- Перевод десятичного числа в двоичную систему счисления:
Для перевода десятичного числа 42 в двоичную систему счисления, мы делим число на 2 и записываем остатки от деления. Затем, считываем эти остатки снизу вверх и получаем двоичное представление числа 42, которое равно 101010.
-
- Перевод рационального числа в десятичную дробь:
Для перевода рационального числа 3/4 в десятичную дробь, мы делим числитель на знаменатель. В данном случае 3 делится на 4, что равно 0.75. Таким образом, рациональное число 3/4 в десятичной форме равно 0.75.
-
- Перевод алгебраического выражения в постфиксную запись:
Для перевода алгебраического выражения (2 + 3) * 4 в постфиксную запись, мы используем обратную польскую запись. В данном случае, постфиксная запись будет 2 3 + 4 *.
-
- Перевод прямоугольных координат в полярные координаты:
Для перевода прямоугольных координат (3, 4) в полярные координаты, мы используем формулы преобразования. Расстояние до начала координат (радиус) равно √(3^2 + 4^2) = 5, а угол между положительным направлением оси x и линией, соединяющей точку с началом координат (аргумент), равен arctan(4/3). Таким образом, прямоугольные координаты (3, 4) в полярной форме равны (5, arctan(4/3)).



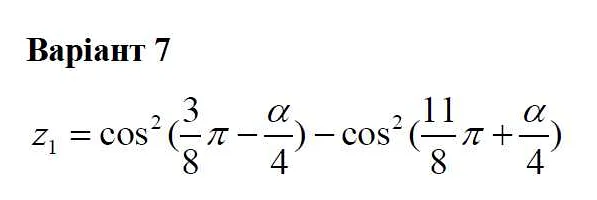
Статья очень интересная и познавательная! Я всегда задумывался, как переводить математические выражения на русский язык. Автор хорошо объяснил, что перевод в математике — это процесс замены математических символов словами. Примеры, которые приведены в статье, помогли мне лучше понять этот процесс. Теперь я знаю, что «сумма» означает «+», «произведение» — «*», «разность» — «-» и «частное» — «/». Также автор указал на необходимость использования скобок для уточнения порядка операций и предложил несколько полезных советов по переводу сложных выражений. В целом, статья очень полезна для всех, кто интересуется математикой. Большое спасибо автору за такой подробный и понятный материал!
Статья на тему «Перевод в математике: определение и примеры» дает хорошее представление о том, что такое перевод в математике и как он применяется. Перевод — это процесс изменения или преобразования числа или выражения из одной формы в другую, без изменения его значения. Это очень полезный инструмент в решении математических задач, так как позволяет упростить выражения или сделать их более подходящими для дальнейших вычислений. Статья содержит примеры простого перевода, такие как перевод десятичной дроби в проценты или обратно, что помогает понять, как применять этот инструмент на практике. Я нашла эту статью очень полезной и информативной, она помогла мне лучше понять и усвоить материал о переводе в математике.