Что обозначает квадрат в математике
Содержимое
Квадрат в математике – это геометрическая фигура, у которой все стороны равны и все углы прямые. В алгебре квадрат – это результат умножения числа на себя. Узнайте больше о свойствах и применении квадрата в математике.
Квадрат является одной из фундаментальных фигур в математике. Он представляет собой геометрическую фигуру, образованную четырьмя равными сторонами и четырьмя прямыми углами. Определение квадрата основывается на его свойствах, которые делают его важным объектом изучения в математике.
Квадрат обладает рядом уникальных свойств. Во-первых, все стороны квадрата равны между собой, что делает его симметричной фигурой относительно всех своих сторон. Во-вторых, углы квадрата равны между собой и равны 90 градусам, что делает его прямоугольником. Квадрат также является регулярным многоугольником, что означает, что все его углы и стороны равны друг другу.
Квадрат имеет широкое применение в различных областях математики и естественных наук. Он является базовой фигурой для изучения геометрии, а его свойства и законы используются в алгебре, тригонометрии и других разделах математики. Кроме того, квадраты часто встречаются в реальном мире, например, в архитектуре, строительстве и дизайне.
Изучение квадрата в математике позволяет развивать абстрактное мышление, улучшать геометрическую интуицию и решать разнообразные задачи. Квадраты играют важную роль в различных математических теориях и моделях, а также находят применение в решении реальных задач. Поэтому понимание значения и свойств квадрата является важным элементом математического образования и научного исследования.
Определение квадрата в математике
Квадрат также может быть определен как частный случай параллелограмма, где все углы равны 90 градусам. Квадрат обладает следующими свойствами:
- Все стороны квадрата равны друг другу.
- Все углы квадрата прямые.
- Диагонали квадрата равны друг другу и пересекаются в точке, делящей их пополам.
- Периметр квадрата равен удвоенной сумме длин его сторон.
- Площадь квадрата равна квадрату длины его стороны.
Квадраты широко применяются в различных областях математики. Они используются для моделирования физических и геометрических объектов, а также в решении задач, связанных с измерением площадей, периметров и объемов.
Видео по теме:
Свойства квадрата
1. Равные стороны: Квадрат имеет четыре равные стороны, что делает его фигурой с симметричной формой.
2. Равные углы: Все углы квадрата равны 90 градусам. Это делает его прямоугольником и параллелограммом одновременно.
3. Диагонали: Диагонали квадрата имеют равную длину и перпендикулярны друг другу. Они делят квадрат на четыре равных треугольника.
4. Площадь: Площадь квадрата равна квадрату длины его стороны. Формула для вычисления площади квадрата: S = a2, где a — длина стороны.
5. Периметр: Периметр квадрата равен четырем его сторонам. Формула для вычисления периметра квадрата: P = 4a, где a — длина стороны.
6. Вписанная окружность: Все четыре вершины квадрата лежат на окружности, которая полностью помещается внутри квадрата. Диаметр этой окружности равен длине стороны квадрата.
7. Описанная окружность: Окружность, проходящая через все четыре вершины квадрата, называется описанной окружностью. Диаметр этой окружности равен длине диагонали квадрата.
8. Симметрия: Квадрат обладает четырьмя осевыми симметриями, проходящими через его центр и середины сторон.
9. Применение: Квадраты широко используются в геометрии, арифметике, физике и других науках. Они являются основой для понимания принципов симметрии, периметра, площади и других математических концепций.
Квадрат в геометрии

Свойства квадрата в геометрии:
- Все стороны квадрата равны
- Все углы квадрата прямые
- Диагонали квадрата равны по длине и перпендикулярны друг другу
- Периметр квадрата равен сумме длин всех четырех его сторон
- Площадь квадрата равна квадрату длины его стороны
Применение квадрата в геометрии:
- Квадрат используется в строительстве и архитектуре для создания прямоугольной формы здания
- Квадрат является основой для создания других геометрических фигур, таких как прямоугольник и ромб
- Квадрат используется в математических моделях и задачах для изучения свойств геометрических фигур и решения уравнений
Квадрат в алгебре
Для обозначения квадрата числа используется символ «^2». Например, квадрат числа 3 обозначается как 3^2, и результат равен 9.
Квадраты чисел имеют ряд свойств:
- Квадрат любого числа всегда положителен или равен нулю.
- Квадрат отрицательного числа равен квадрату его положительного значения.
- Квадрат суммы двух чисел равен сумме квадратов этих чисел и удвоенному произведению этих чисел.
- Квадрат разности двух чисел равен разности квадратов этих чисел и удвоенному произведению этих чисел.
Квадраты чисел имеют широкое применение в алгебре, физике, геометрии и других областях науки. Например, они используются для нахождения площадей и периметров квадратных фигур, в решении уравнений и систем уравнений, а также в расчетах при моделировании и анализе данных.
Квадрат в теории вероятностей
Одно из основных свойств квадрата случайной величины заключается в том, что для неотрицательных случайных величин ее квадрат также будет неотрицательным. Это свойство широко используется при анализе и моделировании случайных процессов.
Квадрат величины в теории вероятностей также используется для определения различных распределений вероятностей. Например, для нормально распределенной случайной величины, квадрат является хи-квадрат распределением. Также квадрат некоторых распределений используется для проверки гипотез и статистического анализа данных.
Квадрат в теории вероятностей имеет широкое применение в решении задач, связанных с вероятностным моделированием, статистикой и анализом данных. Понимание свойств и применение квадрата в теории вероятностей позволяет более точно описывать случайные явления и прогнозировать их результаты.
Квадрат в физике
Одно из основных свойств квадрата в физике — это его связь с площадью поверхности. Поверхность квадрата имеет форму прямоугольника, у которого все стороны равны между собой. Из этого следует, что площадь поверхности квадрата можно вычислить, умножив длину одной из его сторон на саму себя.
Квадрат также используется для определения площади фигур, которые имеют форму квадрата, например, прямоугольника. Если известны длины сторон прямоугольника, можно вычислить его площадь, умножив длину одной стороны на длину другой стороны. Таким образом, квадрат позволяет связать понятие площади с геометрическими фигурами.
Еще одним применением квадрата в физике является его использование в формулах для вычисления площади поверхности тела. Например, для вычисления площади боковой поверхности цилиндра нужно умножить периметр основания на высоту. Периметр основания цилиндра равен сумме длин всех его сторон, которые образуют квадрат.
Таким образом, квадрат в физике является важным инструментом для вычисления площади поверхности различных фигур и связывает геометрию с физикой. Знание и понимание этого понятия позволяет более глубоко изучать различные аспекты физики и применять их на практике.
Применение квадрата в практических задачах
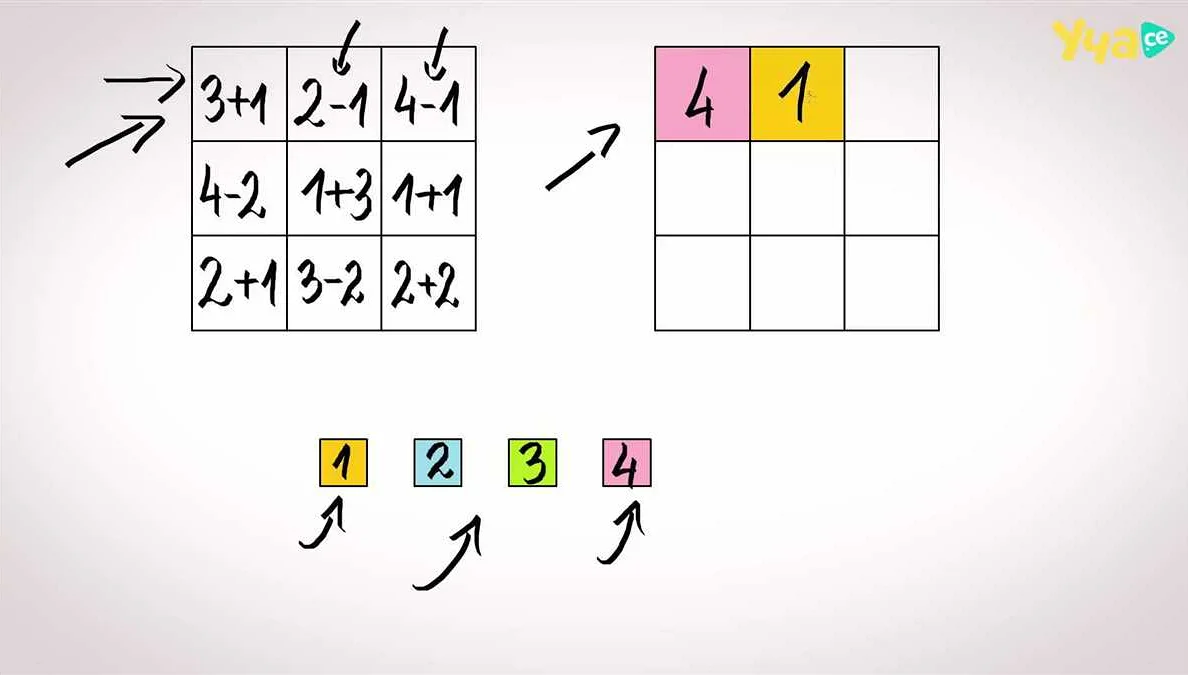
Квадрат имеет множество применений в различных практических задачах. Его свойства и характеристики делают его полезным в различных областях, таких как геометрия, физика, экономика и другие.
Одной из самых распространенных задач, в которых используется квадрат, является вычисление площади. Площадь квадрата вычисляется по формуле: S = a^2, где a — длина стороны квадрата. Эта формула позволяет нам определить площадь квадрата, что может быть полезно, например, при планировании использования земли или расчете площади комнаты.
Квадрат также широко применяется в геометрии для решения задач на подобие фигур. Если две фигуры подобны, то соотношение их площадей равно квадрату соотношения их сторон. Это свойство позволяет нам находить площадь сложных фигур, разбивая их на простые квадраты и суммируя их площади.
Еще одно практическое применение квадрата — в физике. Квадрат встречается в формулах для расчета площади поверхности тела, например, при вычислении площади боковой поверхности цилиндра или конуса. Также квадрат используется в формуле для расчета кинетической энергии тела, где скорость тела возведена в квадрат.
Область примененияПример задачи
| Экономика | Расчет площади сельскохозяйственных угодий |
| Физика | Расчет кинетической энергии тела |
| Геометрия | Вычисление площади сложной фигуры |
Таким образом, квадрат имеет широкое применение и является важным инструментом для решения практических задач в различных областях. Понимание его свойств и применение формул позволяют нам решать задачи эффективно и точно.
Вопрос-ответ:
Что такое квадрат в математике?
В математике квадрат – это число, умноженное само на себя. Квадрат обозначается символом «^2» или через возведение в квадрат.
Какие свойства имеет квадрат числа?
Квадрат числа всегда положителен или равен нулю. Квадрат любого числа является неотрицательным числом и всегда больше или равен нулю. Например, квадрат числа 5 равен 25, а квадрат числа -3 равен 9.
Как можно применить понятие квадрата в реальной жизни?
Понятие квадрата имеет широкое применение в реальной жизни. Например, в геометрии квадрат является одной из основных фигур, а площадь квадрата используется для вычисления площади земельных участков, строительства и т.д. Также квадрат используется в физике для вычисления площади поверхности, объема и т.д.
Как найти квадрат числа?
Чтобы найти квадрат числа, нужно это число умножить само на себя. Например, чтобы найти квадрат числа 7, нужно умножить 7 на 7, что равно 49. Таким образом, квадрат числа 7 равен 49.
Как найти корень из квадрата числа?
Для нахождения корня из квадрата числа нужно извлечь корень из этого числа. Например, чтобы найти корень из квадрата числа 25, нужно извлечь корень квадратный из 25, что равно 5. Таким образом, корень из квадрата числа 25 равен 5.
Что такое квадрат в математике?
В математике квадрат — это фигура, состоящая из четырех равных сторон и четырех прямых углов. Каждая сторона квадрата имеет одинаковую длину.
Какие свойства имеет квадрат?
Квадрат обладает несколькими свойствами. Одно из основных свойств квадрата — все его стороны равны друг другу. Также все углы квадрата прямые, а диагонали равны и перпендикулярны друг другу.




Статья очень интересная и информативная! Никогда не задумывался о значении квадрата в математике. Очень понравилось, что автор начал со введения и определения квадрата. Я узнал много новых свойств, которые раньше не знал. Особенно меня заинтересовало, что квадрат можно использовать для решения уравнений и построения графиков. Это очень полезно в реальной жизни и в работе. Я теперь смогу применять эти знания в практике. Было бы здорово, если бы автор добавил больше примеров и задач для практики. Тем не менее, статья дает хорошее представление о значении квадрата в математике. Я рекомендую ее всем, кто интересуется математикой и хочет узнать больше о квадратах.
Отличная статья! Квадрат — одна из самых основных и важных операций в математике. Он помогает нам вычислять площадь и периметр различных фигур, а также решать уравнения и неравенства. Кроме того, квадрат имеет множество свойств, которые можно применять в различных ситуациях. Например, мы можем разложить квадрат на сумму двух квадратов или вынести общий множитель за скобки. Это очень полезные навыки, которые пригодятся не только в школе, но и в повседневной жизни. Все эти знания помогут нам лучше понимать и решать задачи, а также развивать логическое мышление. В общем, знание квадрата — важный инструмент в арсенале любого математика!
Квадрат является одним из основных понятий в математике и имеет большое значение в различных областях жизни. Квадрат определяется как фигура, у которой все стороны равны и углы прямые. Он обладает рядом интересных свойств, которые широко применяются в различных задачах и расчетах. Одно из основных свойств квадрата — равенство диагоналей. Это означает, что диагонали квадрата равны между собой. Благодаря этому свойству мы можем, например, легко найти длину диагонали, зная длину одной из сторон. Квадрат также обладает свойством равности площадей. Это значит, что площадь квадрата равна квадрату длины его стороны. Это свойство активно используется при решении задач на нахождение площади квадрата или нахождение длины его стороны. Квадраты имеют широкое применение не только в математике, но и в других науках и практических задачах. Например, они используются в архитектуре и строительстве для расчета площади помещений или земельных участков. Они также широко применяются в физике для решения задач связанных с площадью, объемом и другими параметрами различных объектов. Таким образом, квадрат является важным понятием в математике и имеет множество свойств и применений. Понимание и использование этих свойств позволяет решать различные задачи и применять математические знания в практической деятельности.
Квадрат — одно из основных понятий в математике, которое имеет широкое применение и важное значение. Определение квадрата простое — это фигура с четырьмя равными сторонами и углами в 90 градусов. Квадрат обладает рядом уникальных свойств, которые делают его особенным. Во-первых, площадь квадрата можно вычислить, умножив длину его стороны на саму себя. Это позволяет нам рассчитывать площадь подобных фигур и решать множество задач в геометрии и физике. Во-вторых, квадрат является регулярным многоугольником, что означает, что все его стороны и углы равны. Это свойство делает квадрат удобным инструментом для измерений и построений. Квадраты также широко применяются в алгебре, где они используются для решения уравнений и описания геометрических объектов. Таким образом, понимание значения квадрата в математике является важным для развития математических навыков и решения различных задач.
Квадрат в математике – это одна из основных и наиболее известных операций. Она имеет множество свойств и применений, которые необходимы во многих областях жизни. Квадрат числа можно определить как умножение числа на само себя. Например, квадрат числа 5 равен 25. Это позволяет решать множество задач, связанных с измерением площадей, расчетом длин сторон геометрических фигур и т.д. Также квадраты чисел используются в физике, экономике, программировании и других науках. Например, в физике квадраты скорости используются для определения кинетической энергии, а в программировании квадраты чисел могут использоваться для оптимизации алгоритмов и вычислений. В общем, значение квадрата в математике несомненно очень важно и его применение широко распространено в различных сферах нашей жизни.