Что такое площадь математика 4 класс
Содержимое
Площадь в математике для 4 класса — это понятие, которое позволяет измерить площадь поверхности фигуры. Ученикам в 4 классе объясняют, как найти площадь прямоугольника, квадрата и других простых фигур. В этой статье вы найдете основные понятия и примеры решения задач на площадь в математике для 4 класса.
Площадь — это одно из ключевых понятий в математике, которое изучается уже в 4 классе. Понимание площади является важным шагом в обучении геометрии и помогает решать различные задачи, связанные с измерениями и пространством.
Определение площади заключается в измерении площади поверхности фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры (см^2) или квадратные метры (м^2). Понимание площади позволяет рассчитывать и сравнивать размеры различных фигур.
Например, площадь прямоугольника можно найти, умножив длину на ширину. Если прямоугольник имеет длину 5 см и ширину 3 см, то его площадь будет равна 15 квадратным сантиметрам (5 см * 3 см = 15 см^2).
Для нахождения площади квадрата необходимо возвести его сторону в квадрат. Например, если сторона квадрата равна 4 см, то его площадь будет равна 16 квадратным сантиметрам (4 см * 4 см = 16 см^2).
Понимание площади позволяет решать задачи, связанные с измерением площадей различных фигур и нахождением неизвестных параметров. Знание площади помогает ученикам развивать логическое мышление и аналитические навыки, а также применять их на практике в решении задач разной сложности.
Что такое площадь?

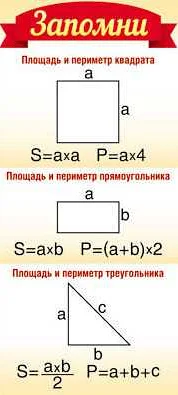
Для различных фигур существуют разные способы вычисления площади. Например, для прямоугольника площадь вычисляется как произведение длины одной стороны на длину другой стороны. Для квадрата площадь вычисляется как квадрат длины одной из его сторон. Для треугольника площадь вычисляется как половина произведения длины основания на высоту.
Понимание площади позволяет нам измерять и сравнивать поверхности разных фигур, а также решать задачи, связанные с площадью. Знание площади помогает нам, например, рассчитать площадь комнаты, посадочной площадки или поля.
Изучение площади является важным элементом математического образования, и оно помогает развивать логическое мышление, абстрактное мышление и навыки решения задач.
Определение площади в математике 4 класс
Для определения площади различных фигур в математике 4 класса используются различные формулы. Например, для прямоугольника площадь можно найти, умножив длину одной стороны на длину другой стороны. Для квадрата площадь можно найти, возведя в квадрат длину одной из его сторон.
Определение площади в математике 4 класс включает также изучение площади треугольника. Для треугольника существует формула площади, которая зависит от длин его сторон или от длины одной стороны и высоты, опущенной на эту сторону. Также существуют специальные формулы для определения площади параллелограмма, трапеции, ромба и других фигур.
Изучение площади в математике 4 класс является важным компонентом развития геометрического мышления. Умение определять площадь различных фигур помогает развивать навыки анализа и решения задач, а также понимание пространственных отношений между объектами.
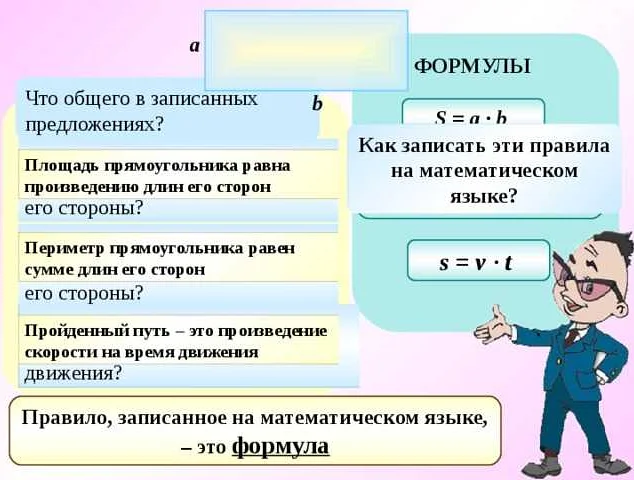
Формула для вычисления площади

Для прямоугольника площадь можно вычислить по формуле: S = a * b, где a – длина стороны прямоугольника, b – ширина стороны прямоугольника.
Для квадрата площадь можно вычислить также по формуле: S = a * a, где a – длина стороны квадрата.
Для треугольника площадь можно вычислить по формуле: S = (a * h) / 2, где a – длина основания треугольника, h – высота треугольника, опущенная на основание.
Для круга площадь можно вычислить по формуле: S = π * r * r, где π – математическая константа, примерное значение которой равно 3.14, r – радиус окружности.
Зная формулы для вычисления площади разных фигур, можно легко решать задачи на нахождение площади и работать с различными геометрическими фигурами.
Как измерить площадь?

Для измерения площади необходимо знать форму объекта, площадь которого нужно найти. Существуют разные методы для измерения площади различных фигур.
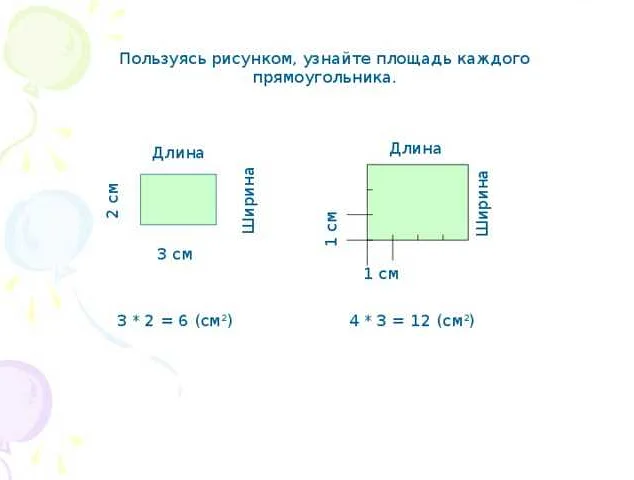
Для нахождения площади прямоугольника необходимо измерить длину одной из сторон и умножить ее на длину второй стороны.
Площадь квадрата можно найти, умножив длину одной из его сторон на саму себя.
Для нахождения площади треугольника нужно умножить длину основания на высоту и разделить полученное значение на 2.
Для измерения площади круга необходимо знать радиус или диаметр. Площадь круга можно найти по формуле: площадь = π * радиус^2, где π (пи) — математическая константа, примерное значение которой равно 3.14.
Для других фигур существуют свои специфические методы измерения площади, которые можно найти в специальной литературе или в Интернете.
Измерение площади является важным навыком в математике, который помогает решать различные задачи, связанные с геометрией и практическими применениями.
Площадь прямоугольника

Для вычисления площади прямоугольника необходимо умножить длину одной из его сторон на длину другой стороны:
Площадь = Длина * Ширина
Например, если у прямоугольника длина равна 5 см, а ширина — 3 см, то его площадь будет равна 5 * 3 = 15 квадратных сантиметров.
Таким образом, вычисление площади прямоугольника сводится к простой операции умножения длины на ширину, что делает его одной из самых простых фигур для вычисления площади.
Площадь квадрата
Площадь квадрата — это мера площади внутри квадрата. Она показывает, сколько квадратных единиц умещается внутри этой фигуры.
Чтобы найти площадь квадрата, нужно умножить длину одной его стороны на саму себя.
Например, если сторона квадрата равна 5 сантиметров, то площадь квадрата будет равна 5 * 5 = 25 квадратных сантиметров.
Площадь квадрата измеряется в квадратных единицах площади, таких как квадратные сантиметры (см²), квадратные метры (м²) и т.д.
Зная площадь квадрата, можно также найти длину его стороны. Для этого нужно извлечь квадратный корень из площади.
Например, если площадь квадрата равна 16 квадратных сантиметров, то его сторона будет равна √16 = 4 сантиметра.
Площадь треугольника
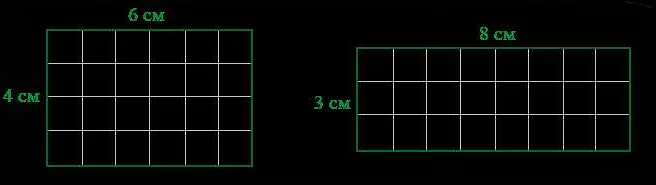
Существует несколько способов вычисления площади треугольника:
- Площадь треугольника можно вычислить, зная длину его основания и высоту, проведенную к основанию. Формула для этого метода выглядит следующим образом: площадь = (основание * высота) / 2.
- Если известны длины всех трех сторон треугольника, можно воспользоваться формулой Герона для вычисления площади. Формула Герона выглядит следующим образом: площадь = √(полупериметр * (полупериметр — сторона1) * (полупериметр — сторона2) * (полупериметр — сторона3)), где полупериметр равен сумме всех сторон, деленной на 2.
- Если известны координаты вершин треугольника на плоскости, можно воспользоваться формулой для вычисления площади треугольника по координатам. Для этого требуется знание алгебры и геометрии.
Зная площадь треугольника, мы можем использовать эту информацию для решения различных задач, связанных с геометрией и планированием.
Площадь круга
Формула для вычисления площади круга — это πr², где π (пи) — это математическая константа, примерное значение которой равно 3,14159, а r — радиус круга. Радиус — это расстояние от центра круга до любой точки на его окружности.
Пример расчета площади круга:
- Задан радиус круга, например, 5 см.
- Используя формулу πr², вычисляем площадь круга: π × 5² = 3,14159 × 25 = 78,54.
Таким образом, площадь круга с радиусом 5 см равна 78,54 квадратных сантиметров.
Вопрос-ответ:
Что такое площадь в математике?
Площадь в математике — это мера площади поверхности фигуры, которая определяется как число квадратных единиц, которые могут поместиться внутри этой фигуры.
Как определить площадь прямоугольника?
Для определения площади прямоугольника необходимо умножить длину одной из его сторон на длину второй стороны.
Как определить площадь треугольника?
Для определения площади треугольника необходимо умножить длину одной из его сторон на половину длины высоты, опущенной на эту сторону.
Как определить площадь круга?
Для определения площади круга необходимо умножить квадрат радиуса на число Пи (π).
Как определить площадь параллелограмма?
Для определения площади параллелограмма необходимо умножить длину одной из его сторон на высоту, опущенную на эту сторону.