Почему математический маятник проходя положение равновесия продолжает свое движение
Содержимое
- 1 Почему математический маятник проходя положение равновесия продолжает свое движение
- 1.1 Сила тяжести влияет на математический маятник
- 1.2 Роль силы тяжести в движении математического маятника
- 1.3 Математический маятник в положении равновесия
- 1.4 Закон сохранения энергии в математическом маятнике
- 1.5 Кинетическая и потенциальная энергия в движении математического маятника
- 1.6 Математический маятник: простые гармонические колебания
- 1.7 Влияние длины нити на период колебаний математического маятника
- 1.8 Математический маятник: амплитуда и частота колебаний
- 1.9 Вопрос-ответ:
- 1.9.0.1 Почему математический маятник продолжает двигаться, находясь в положении равновесия?
- 1.9.0.2 Почему математический маятник не останавливается в положении равновесия?
- 1.9.0.3 Почему математический маятник не останавливается в положении равновесия, если внешних сил нет?
- 1.9.0.4 Почему математический маятник продолжает двигаться, находясь в положении равновесия, несмотря на силу тяжести?
- 1.9.0.5 Что происходит с математическим маятником, находящимся в положении равновесия, со временем?
- 1.10 Видео по теме:
Узнайте, почему математический маятник, достигнув положение равновесия, не останавливается, а продолжает двигаться. Разберем, какие факторы влияют на его движение и почему он не останавливается без внешнего воздействия. Разберем основные принципы работы математического маятника и его динамику.
Математический маятник – это устройство, состоящее из груза, подвешенного на невесомой нити и способное осуществлять колебания по горизонтальной оси. Интересным явлением является то, что даже когда маятник находится в положении равновесия, он все равно продолжает двигаться. Это явление может показаться странным, однако оно объяснимо с помощью принципа сохранения энергии.
Когда математический маятник находится в положении равновесия, потенциальная энергия груза достигает максимального значения, а его кинетическая энергия оказывается равной нулю. Однако, из-за взаимодействия маятника с окружающей средой (например, сопротивления воздуха), энергия постепенно теряется.
В силу закона сохранения энергии, энергия, теряемая в результате сопротивления, должна быть компенсирована другими формами энергии. В данном случае, потенциальная энергия груза превращается в кинетическую энергию и наоборот. Это приводит к тому, что маятник продолжает колебаться даже в положении равновесия.
Сила тяжести влияет на математический маятник
Математический маятник представляет собой идеализированную систему, состоящую из точечной массы, подвешенной на нерастяжимом нитевидном подвесе. В положении равновесия маятник находится, когда нить вертикальна и масса находится в покое.
Однако, даже находясь в положении равновесия, математический маятник продолжает двигаться из-за влияния силы тяжести. Сила тяжести направлена вертикально вниз и оказывает постоянное воздействие на массу маятника.
В своем движении математический маятник проходит через точку равновесия, где сила тяжести направлена вниз и сила натяжения нити направлена вверх. В этот момент все силы, действующие на массу, сбалансированы и маятник находится в покое.
Однако, как только масса маятника отклоняется от точки равновесия, сила тяжести начинает оказывать влияние. Она придает массе ускорение, направленное в сторону положения равновесия. Ускорение массы приводит к ее движению, и маятник начинает колебаться.
Таким образом, сила тяжести играет ключевую роль в движении математического маятника. Она вызывает ускорение массы и обеспечивает его движение даже в положении равновесия.
Роль силы тяжести в движении математического маятника
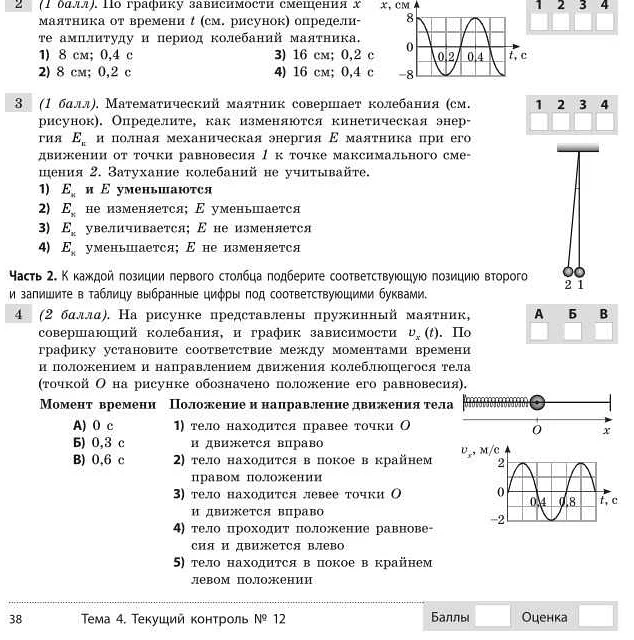
Сила тяжести — это сила, с которой Земля притягивает все объекты к своему центру. В случае математического маятника, сила тяжести действует на точечную массу, создавая ускорение, направленное в сторону центра Земли.
Когда математический маятник находится в положении равновесия, сила тяжести и сила натяжения нити сбалансированы. Сила натяжения нити направлена в сторону центра масс маятника и предотвращает его падение. В то же время, сила тяжести, направленная вниз, пытается вернуть маятник к положению равновесия.
Из-за силы тяжести математический маятник начинает двигаться в сторону, противоположную его начальному отклонению. При этом, сила тяжести обеспечивает ускорение маятника и изменяет его кинетическую и потенциальную энергию.
Во время движения, сила тяжести непрерывно действует на математический маятник, изменяя его скорость и направление движения. Но на каждом положении маятника, когда он достигает крайней точки, сила тяжести снова сбалансирована силой натяжения нити, и маятник возвращается к положению равновесия.
Таким образом, роль силы тяжести в движении математического маятника заключается в создании ускорения, направленного в сторону центра Земли, которое обеспечивает движение маятника и его возвращение к положению равновесия.
Математический маятник в положении равновесия
Математический маятник представляет собой систему, состоящую из точки подвеса и груза, подвешенного на нити или стержне. Положение равновесия математического маятника достигается, когда груз находится в определенном положении, в котором сила тяжести груза равна центростремительной силе, действующей на него.
При нахождении в положении равновесия, математический маятник не испытывает никаких внешних сил или моментов, которые могли бы его возбудить и вызвать движение. Однако, даже в положении равновесия математический маятник может продолжать двигаться, если есть начальное отклонение от положения равновесия.
Это связано с тем, что математический маятник является системой с запасенной энергией. При отклонении от положения равновесия, груз приобретает потенциальную энергию, которая преобразуется в кинетическую энергию при движении груза вниз. При достижении максимальной скорости груза вниз, кинетическая энергия преобразуется обратно в потенциальную энергию при движении груза вверх.
Таким образом, при нахождении в положении равновесия, математический маятник продолжает двигаться за счет сохранения энергии и преобразования ее из одной формы в другую. Этот процесс будет продолжаться до тех пор, пока не будет исчерпана запасенная энергия и маятник не вернется в положение равновесия.
Закон сохранения энергии в математическом маятнике
Маятник имеет потенциальную энергию, которая зависит от его положения. Если маятник отклоняется от положения равновесия, его потенциальная энергия превращается в кинетическую энергию. По мере того, как маятник движется обратно к положению равновесия, кинетическая энергия превращается обратно в потенциальную энергию.
Закон сохранения энергии утверждает, что сумма кинетической и потенциальной энергии в системе остается постоянной. Это означает, что когда маятник достигает крайней точки своего движения, его потенциальная энергия максимальна, а кинетическая энергия минимальна. По мере приближения к положению равновесия, потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
При достижении положения равновесия, потенциальная энергия полностью превращается в кинетическую энергию, и маятник продолжает двигаться с постоянной скоростью. В этом положении сумма кинетической и потенциальной энергии достигает своего минимума. Движение маятника будет продолжаться до тех пор, пока не будет применена внешняя сила или пока не будет потеряна энергия из-за трения и других сопротивлений.
Таким образом, закон сохранения энергии играет важную роль в движении математического маятника, обеспечивая его постоянную скорость и сохранение энергии в системе.
Кинетическая и потенциальная энергия в движении математического маятника

Математический маятник представляет собой тяжелое невесомое тело, закрепленное на невесомой нерастяжимой нити, которая крепится к точке подвеса. При движении маятника возникают изменения в его потенциальной и кинетической энергии.
Потенциальная энергия математического маятника связана с его положением относительно положения равновесия. В точке максимального отклонения маятника от положения равновесия его потенциальная энергия достигает максимального значения. По мере приближения к положению равновесия, потенциальная энергия уменьшается. В положении равновесия потенциальная энергия математического маятника минимальна.
Кинетическая энергия математического маятника связана с его движением. Когда маятник отклоняется от положения равновесия и начинает двигаться, его потенциальная энергия уменьшается, а кинетическая энергия увеличивается. По мере приближения к положению равновесия, кинетическая энергия уменьшается, а потенциальная энергия увеличивается. В положении равновесия кинетическая энергия математического маятника равна нулю.
Движение математического маятника подчиняется закону сохранения механической энергии, согласно которому сумма кинетической и потенциальной энергии остается постоянной на протяжении всего движения. Поэтому, даже находясь в положении равновесия, математический маятник продолжает двигаться, переходя из состояния полной потенциальной энергии в состояние полной кинетической энергии и обратно.
Математический маятник: простые гармонические колебания
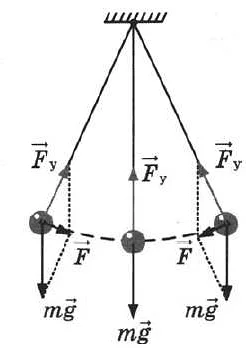
Математический маятник может находиться в положении равновесия, когда его точка подвеса находится внизу. В этом положении сила тяжести направлена вниз, а натяжение нити направлено вверх, и эти силы компенсируют друг друга.
Однако, даже находясь в положении равновесия, математический маятник продолжает двигаться. Это связано с тем, что в момент отклонения точки подвеса от положения равновесия, возникает сила возвратная, направленная в сторону положения равновесия.
Эта сила называется возвратной силой и она пропорциональна отклонению точки подвеса от положения равновесия. Чем больше отклонение, тем сильнее возвратная сила, стремящаяся вернуть точку подвеса в положение равновесия.
При движении математического маятника возникают простые гармонические колебания. Это означает, что маятник совершает равномерные колебания вокруг положения равновесия. Период колебаний и амплитуда зависят от длины нити и начальной амплитуды отклонения.
Таким образом, математический маятник продолжает двигаться, находясь в положении равновесия, из-за воздействия возвратной силы, которая стремится вернуть его в положение равновесия. Это явление проявляется в виде простых гармонических колебаний.
Влияние длины нити на период колебаний математического маятника
По закону сохранения энергии, математический маятник будет колебаться вокруг положения равновесия до тех пор, пока энергия колебаний будет сохраняться и переходить из кинетической в потенциальную и обратно. Длина нити оказывает влияние на период колебаний, так как она определяет скорость, с которой маятник движется, и высоту, на которую он поднимается в каждый момент времени.
Оказывается, что период колебаний математического маятника прямо пропорционален квадратному корню из длины нити. Это можно выразить следующей формулой:
T = 2π√(L/g)
где T — период колебаний, L — длина нити, g — ускорение свободного падения (приближенно равное 9,8 м/с² на Земле).
Таким образом, при увеличении длины нити математического маятника, его период колебаний будет увеличиваться. Это связано с тем, что при большей длине нити маятник будет двигаться медленнее и подниматься на большую высоту в каждый момент времени.
Изучение влияния длины нити на период колебаний математического маятника позволяет более глубоко понять его механизм работы и использовать эту информацию при проектировании и расчете подвесных систем, таких как маятники и качели.
Математический маятник: амплитуда и частота колебаний
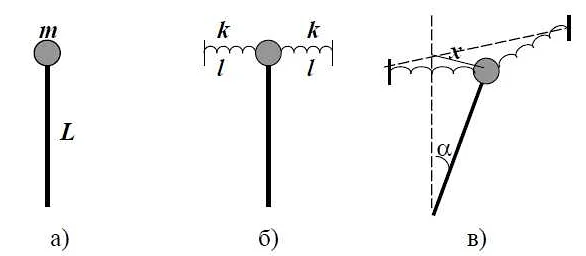
Амплитуда колебаний — это максимальное отклонение маятника от положения равновесия. Она определяется начальными условиями системы — начальной скоростью и начальным отклонением от положения равновесия. Чем больше начальное отклонение, тем больше амплитуда колебаний. Однако, при увеличении амплитуды, возникают дополнительные факторы — сопротивление воздуха и трение в точке подвеса, которые могут влиять на длительность колебаний.
Частота колебаний — это количество колебаний, совершаемых маятником за единицу времени. Она зависит от длины нити и ускорения свободного падения. Чем длиннее нить, тем меньше частота колебаний. Чем больше ускорение свободного падения, тем больше частота колебаний. Частота колебаний также может быть выражена через период колебаний — время, за которое маятник осуществляет одно полное колебание.
Математический маятник является примером гармонического осциллятора, который описывается математическими уравнениями. Он используется во многих областях, включая физику, инженерию и астрономию. Изучение амплитуды и частоты колебаний математического маятника позволяет понять его свойства и применение в различных задачах.
Вопрос-ответ:
Почему математический маятник продолжает двигаться, находясь в положении равновесия?
Математический маятник продолжает двигаться, находясь в положении равновесия, потому что он имеет некоторую начальную скорость. Эта скорость позволяет маятнику преодолевать силу гравитации и продолжать движение.
Почему математический маятник не останавливается в положении равновесия?
Математический маятник не останавливается в положении равновесия из-за сохранения энергии. При движении маятник сохраняет свою механическую энергию, и эта энергия переходит из кинетической (движение) в потенциальную (высота). Этот процесс продолжается до полной остановки маятника.
Почему математический маятник не останавливается в положении равновесия, если внешних сил нет?
Математический маятник не останавливается в положении равновесия, даже если внешних сил нет, из-за влияния диссипативных сил. Диссипативные силы, такие как сопротивление воздуха или трение в подвесе маятника, приводят к потере энергии и замедлению движения маятника.
Почему математический маятник продолжает двигаться, находясь в положении равновесия, несмотря на силу тяжести?
Математический маятник продолжает двигаться, находясь в положении равновесия, несмотря на силу тяжести, из-за действия инерции. Инерция — это свойство тела сохранять свое состояние движения или покоя. Таким образом, маятник сохраняет свою начальную скорость и продолжает двигаться даже в положении равновесия.
Что происходит с математическим маятником, находящимся в положении равновесия, со временем?
Со временем математический маятник, находящийся в положении равновесия, замедляется и останавливается из-за влияния диссипативных сил. Диссипативные силы, такие как сопротивление воздуха и трение в подвесе маятника, постепенно снижают энергию маятника, приводя к его остановке.
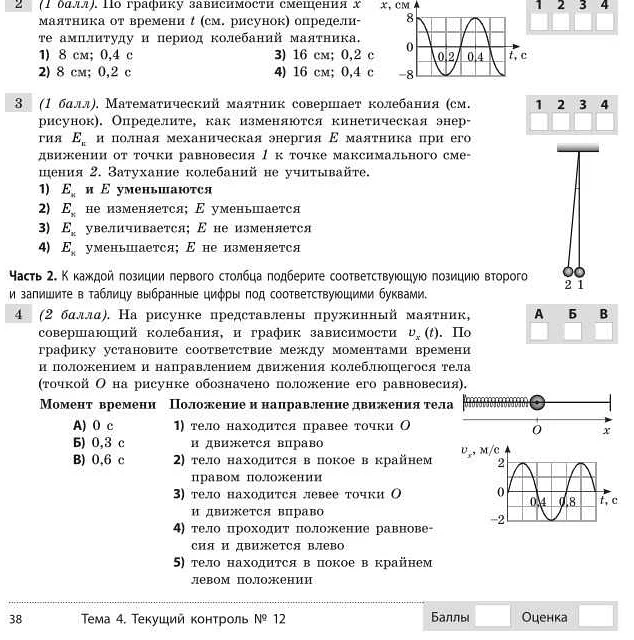



Математический маятник продолжает двигаться, находясь в положении равновесия, потому что существует сила, называемая центробежной силой, которая действует на маятник и заставляет его двигаться. Эта сила возникает из-за инерции массы маятника, которая стремится сохранить свое движение. Когда математический маятник находится в положении равновесия, он находится в точке, где силы, действующие на маятник, сбалансированы. В таком положении сила тяжести, действующая на маятник, направлена вниз, а центробежная сила направлена в сторону, перпендикулярную к направлению силы тяжести. Центробежная сила действует как поперечная сила, удерживая маятник в положении равновесия. Если сила тяжести превышает силу центробежной силы, маятник начнет двигаться вниз, увеличивая свою потенциальную энергию. Затем, когда маятник достигнет самой нижней точки, потенциальная энергия будет максимальной, а кинетическая энергия будет минимальной. Затем цикл повторяется, и маятник начинает двигаться в обратную сторону. В этот момент центробежная сила начинает преобладать над силой тяжести, и маятник начинает подниматься, преобразуя свою потенциальную энергию в кинетическую. Верхняя точка движения становится новым положением равновесия, и процесс повторяется снова и снова. Таким образом, математический маятник продолжает двигаться, находясь в положении равновесия, благодаря силе инерции и сбалансированному взаимодействию силы тяжести и центробежной силы. Это простое, но удивительное явление, которое демонстрирует законы физики и математики.
Мне кажется, что математический маятник продолжает двигаться в положении равновесия из-за сохранения энергии. Когда маятник находится в центре, он имеет потенциальную энергию, которая преобразуется в кинетическую энергию, когда он начинает двигаться в сторону. Когда маятник достигает крайней точки, кинетическая энергия достигает максимума, а потенциальная энергия снижается до минимума. Затем, когда маятник возвращается в центр, эти энергии снова меняются местами. Это создает непрерывное колебание, которое поддерживается за счет сохранения энергии. Кроме того, положение равновесия математического маятника обеспечивает баланс сил. Находясь в центре, маятник испытывает силу тяжести, направленную вниз, и силу натяжения нити, направленную вверх. Эти силы равны по модулю и противоположны по направлению, что приводит к равновесию. Однако, даже в положении равновесия, маятник по-прежнему обладает потенциальной энергией, которая может быть использована для продолжения колебаний. В целом, математический маятник продолжает двигаться в положении равновесия из-за сохранения энергии и баланса сил. Это позволяет ему непрерывно колебаться и демонстрировать интересные физические явления.
Математический маятник продолжает двигаться, находясь в положении равновесия, из-за наличия потенциальной энергии в системе. При движении маятника его потенциальная энергия превращается в кинетическую и наоборот. Даже в положении равновесия, когда маятник находится в неподвижном состоянии, потенциальная энергия все еще присутствует в системе. При смещении маятника из положения равновесия, его потенциальная энергия возрастает, а кинетическая энергия уменьшается. Затем, по мере движения маятника в обратном направлении, потенциальная энергия уменьшается, а кинетическая энергия возрастает. Этот процесс повторяется в течение всего времени движения маятника, что позволяет ему продолжать двигаться, даже находясь в положении равновесия. Также следует упомянуть о важной роли силы трения. Ее наличие приводит к постепенному затуханию колебаний маятника и, в конечном итоге, к его остановке. Однако, при отсутствии трения, математический маятник мог бы продолжать колебаться вечно. Таким образом, математический маятник продолжает двигаться, находясь в положении равновесия, благодаря преобразованию потенциальной и кинетической энергии внутри системы. Это явление интересно и удивительно, и именно из-за него мы можем наблюдать красивые колебания маятника.
Математический маятник продолжает двигаться находясь в положении равновесия из-за законов сохранения энергии и момента импульса. В положении равновесия маятник находится в стационарном состоянии, а его положение и скорость остаются постоянными. Однако, даже при отсутствии внешних сил, маятник не может остановиться полностью из-за некоторых факторов. Во-первых, из-за трения в оси подвеса и воздуха, возникает диссипация энергии, что приводит к постепенному затуханию колебаний маятника. Таким образом, его движение будет продолжаться, но с постепенным замедлением. Во-вторых, из-за неидеальности самого маятника, он испытывает некоторые внутренние потери энергии. Например, маятник может быть изготовлен из материала с определенным коэффициентом затухания, который приводит к потере энергии в виде тепла или звука. Таким образом, хотя математический маятник может находиться в положении равновесия, его движение не может быть бесконечным. Время, в течение которого маятник будет колебаться, зависит от множества факторов, включая трение, неидеальность маятника и начальные условия.
Математический маятник продолжает двигаться в положении равновесия из-за закона сохранения энергии. Когда маятник находится в точке максимального отклонения, он обладает потенциальной энергией, которая превращается в кинетическую энергию, когда маятник проходит через положение равновесия. Затем, когда маятник достигает максимального отклонения в противоположную сторону, кинетическая энергия превращается обратно в потенциальную. Этот процесс продолжается бесконечно, пока нет внешнего воздействия, которое изменит энергию системы. Математический маятник идеализированный объект, который не испытывает трения или других сил сопротивления. Если бы такие силы были присутствовали, то маятник остановился бы со временем. Но благодаря отсутствию сил сопротивления в реальном мире, математический маятник может продолжать двигаться в положении равновесия бесконечно долго. Это свойство математического маятника позволяет использовать его в различных научных и инженерных расчетах, где требуется моделирование системы с колебаниями.