Уравнение математического маятника: как оно описывает его движение?

Уравнение математического маятника описывает его движение и позволяет рассчитать время колебаний, период и амплитуду. Узнайте, какое уравнение стоит за этим интересным явлением в физике!

Математический маятник – универсальный образец колебательного движения, который широко используется в науке и технике. Его движение описывается уравнением, которое дает возможность прогнозировать его поведение и использовать для различных целей, от измерения времени до создания самых сложных конструкций.

Одним из примеров использования уравнения математического маятника является создание часов – так называемых маятниковых часов. Они работают за счет колебания стрелки, закрепленной на маятнике, который движется под действием силы тяжести и сопротивления воздуха. При этом уравнение непрерывно корректируется, чтобы обеспечить точность и стабильность хода часов.

Однако, уравнение математического маятника имеет и более широкое применение. Оно находит свое применение в различных отраслях науки, включая физику, математику, астрономию, геодезию и прочие. Поэтому знание и понимание этого уравнения – необходимый и важный элемент общекультурной компетенции.

Уравнение математического маятника

Математический маятник — это физическая система, которая используется для исследования колебаний. Он является одним из наиболее изученных объектов в физике и широко применяется в научных и инженерных исследованиях. Уравнение математического маятника является одним из самых важных уравнений в физике и описывает движение маятника.

Уравнение математического маятника может быть записано в нескольких формах. Одной из самых распространенных форм является уравнение для малых углов отклонения. Это уравнение имеет вид:

d²θ/dt² + (g/L)θ = 0

где θ — угол отклонения маятника от вертикального положения, g — ускорение свободного падения, а L — длина маятника.

Уравнение математического маятника может быть решено аналитически или численно. Аналитическое решение позволяет получить точные формулы для описания движения маятника, в то время как численное решение используется для моделирования движения маятника в реальном времени.

Уравнение математического маятника имеет множество приложений в конструировании и изучении различных устройств, таких как маятники-часы, гирометры, грузоподъемные краны и даже в переменных токах в электроэнергетике.

Изучение уравнения математического маятника является важным шагом для понимания физических явлений и приложений в различных отраслях науки и технологии.

Что такое математический маятник?

Математический маятник – это изначально абстрактная модель физического процесса. Данный объект представляет собой тело некоторой массы, прикрепленное к точке подвеса нерастяжимой нити. Математический маятник считается простейшей моделью движения, при которой отсутствует вращательное движение.

Взаимодействие тела с окружающей средой, такие факторы как сопротивление воздуха, силы трения, не учитываются в этой модели. Математический маятник помогает описать многие процессы наблюдаемые в природе, такие как колебания пульсаций в кровеносной системе, колебания электромагнитного поля в излучении, а также многие другие физические явления.

Данный объект изучается в рамках курсов математической физики, теории управления, теории систем и многих других дисциплин. Важным свойством математического маятника является его период колебаний.

Период колебаний математического маятника зависит от длины нити и ускорения свободного падения, а также не зависит от массы тела. Данное свойство позволяет описывать колебания многих других объектов, таких как электрические цепи, оптические системы и т.д.

Описание движения математического маятника

Математический маятник — это устройство, которое состоит из точечной массы, подвешенной на невесомой и нерастяжимой нити. При движении такого маятника масса движется по окружности, а нить остается натянутой и поддерживает массу в вертикальном положении.

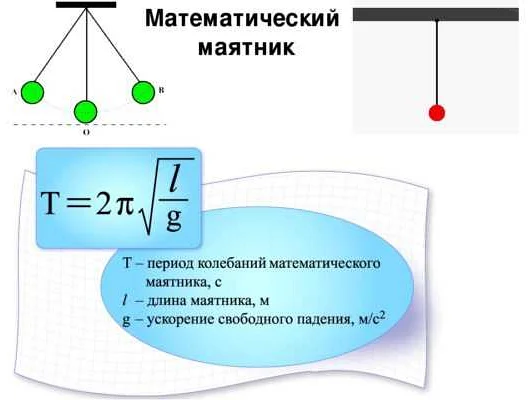
Описать движение математического маятника можно с помощью уравнения маятника, которое выражает зависимость между углом отклонения маятника от вертикали и его периодом колебания. Это уравнение имеет вид:

T = 2π√(L/g)

Здесь T — период колебаний, L — длина нити маятника, а g — ускорение свободного падения.

Особенностью движения математического маятника является то, что период его колебаний не зависит от амплитуды колебаний. Именно поэтому этот тип маятника называется «математическим».

Другим важным параметром для описания движения маятника является его энергия. Маятник имеет два вида энергии — кинетическую и потенциальную. В верхней точке колебаний потенциальная энергия максимальна, а кинетическая — минимальна. В нижней точке колебаний наоборот: кинетическая энергия максимальна, а потенциальная — минимальна.

В целом можно сказать, что движение математического маятника характеризуется периодичностью, равномерностью и сохранением энергии в колебаниях.

Что такое уравнение движения маятника?

Уравнение движения маятника — это математическая формула, которая описывает движение маятника в зависимости от его массы, длины и начальной амплитуды. Уравнение движения маятника позволяет рассчитать скорость и ускорение маятника в каждый момент времени, а также определить его положение и время возвращения к исходной точке.

В классической механике уравнение движения маятника является дифференциальным уравнением второго порядка, где ускорение маятника связано с его положением и скоростью. Решение этого уравнения позволяет точно предсказать движение маятника в любой момент времени.

Уравнение движения маятника является важным инструментом для понимания механических систем, таких как маятники, колебания и осцилляции. Поэтому оно широко используется в научных и инженерных расчетах, например, при проектировании высокоточных часов, приборов измерения времени, оптических систем и многих других устройств.

Важно отметить, что уравнение движения маятника предполагает, что маятник находится в идеальных условиях без трения и воздушного сопротивления. Однако на практике такие условия редко соблюдаются, поэтому при реальном использовании уравнение движения маятника может быть дополнено другими уравнениями, учитывающими факторы внешней среды.

Как формулируется уравнение математического маятника?

Уравнение математического маятника описывает движение твердого тела, подвешенного на невесомой нити и колеблющегося вокруг точки подвеса. Это уравнение позволяет нам понять и предсказать, как будет изменяться положение маятника со временем.

Уравнение математического маятника имеет вид:

θ» + (g/l)sin(θ) = 0

Здесь θ» — это ускорение маятника, g — ускорение свободного падения, l — длина нити, а θ — угол отклонения маятника от вертикального положения.

Это уравнение является одним из самых простых уравнений движения, но при этом оно очень важно в физике и математике. Оно может быть использовано для моделирования колебаний в других системах, от электрических цепей до химических реакций.

Важно отметить, что уравнение математического маятника имеет нелинейный характер, что затрудняет его решение аналитическим методом. Однако существует множество численных методов, которые позволяют решить это уравнение и оценить поведение маятника в различных условиях.

Как использовать уравнение движения маятника в математике?

Уравнение движения маятника является одним из фундаментальных уравнений в математике и физике. Оно используется для описания движения маятника, который представляет собой механическую систему, состоящую из тела и подвески. Уравнение движения маятника позволяет определить угол отклонения маятника от вертикального положения и его скорость в любой момент времени.

Для использования уравнения движения маятника в математике необходимо знать начальные условия системы, т.е. начальный угол отклонения маятника и его начальную скорость. После определения начальных условий, можно решить уравнение движения маятника и получить как функцию угла отклонения маятника от вертикали, так и функцию его скорости.

Уравнение движения маятника широко используется в различных областях науки и техники, включая физику, математику, инженерию, астрономию и другие. Например, на основе уравнения движения маятника можно рассчитать время колебания маятника, его период и частоту. Также уравнение маятника используется для решения задач в сферах, где требуется моделирование механических систем, например, в разработке управляющих систем для роботов или автомобилей.

Использование уравнения движения маятника в математике требует достаточных знаний в области дифференциальных уравнений и математической физики. Однако, даже без глубоких знаний в этих областях, можно ознакомиться с основами уравнения движения маятника и его применениями в различных сферах науки и техники.

Примеры решения уравнения математического маятника

Пример 1: Рассмотрим маятник, который отклоняется на угол 30 градусов. Найдём время, за которое маятник совершит 5 колебаний.

По уравнению математического маятника:

T = 2π√(L/g)

где T – период колебаний маятника, L – длина его подвеса, g – ускорение свободного падения.

Известно, что отклонение от вертикали составляет 30 градусов, а ускорение свободного падения равно 9,8 м/с². Длина подвеса маятника не указана, но мы можем воспользоваться формулой для нахождения длины подвеса:

L = gT² / 4π²

Подставив все известные данные, получим:

L = 9,8 (2 x 5 / 4π²)² / 4π² ≈ 0,742 м

Теперь, подставив найденные значения для L и g в формулу для периода колебаний, получим:

T = 2π√(0,742 / 9,8) ≈ 1,712 секунд

Значит, за 5 колебаний маятник совершит 5 x 1,712 ≈ 8,56 секунд.

Пример 2: Рассмотрим маятник длиной 1 метр. Найдём максимальную скорость маятника при максимальном отклонении от вертикали на угол 20 градусов.

Для начала найдём потенциальную энергию маятника при максимальном отклонении:

Ep = mgh

где m – масса маятника, h – высота маятника относительно точки покоя, g – ускорение свободного падения.

Обозначим высоту маятника относительно точки покоя:

h = L(1 — cosα)

где α – угол отклонения маятника, L – длина подвеса маятника.

Тогда:

Ep = mgh = mgL(1 — cosα)

Для нахождения скорости маятника в максимальной точке воспользуемся законом сохранения энергии:

Ek + Ep = const

где Ek – кинетическая энергия маятника.

В максимальной точке, потенциальная энергия максимальна, поэтому:

Ek = const — mgh

Изначально маятник находится в покое, поэтому его кинетическая энергия равна 0. Находясь в максимальной точке, вся потенциальная энергия переходит в кинетическую. Таким образом,

mgh = ½mv²

где v – скорость маятника в максимальной точке.

Подставляя найденную формулу для потенциальной энергии, получим:

½mv² = mgL(1 — cosα)

Откуда:

v = √(2gL(1 — cosα))

Подставляем известные значения и получаем:

v = √(2 x 9,8 x 1 (1 — cos20)) ≈ 1,95 м/с

Таким образом, максимальная скорость маятника при максимальном отклонении от вертикали на угол 20 градусов составляет 1,95 м/с.

Как применить уравнение движения маятника в реальной жизни?

Уравнение математического маятника имеет широкое применение в реальной жизни, особенно в физике и инженерных науках. Во-первых, оно позволяет рассчитать период колебаний маятника, что важно для создания точных часов и измерительных приборов.

Кроме того, уравнение маятника используется для моделирования колебаний различных систем, например, маятниковых механизмов в механических часах или систем с грузами, подвешенными на пружинах. С помощью уравнения можно определить законы движения этих систем, что позволяет проектировать их более точно и эффективно.

В физике уравнение математического маятника применяется для исследования колебаний механических систем, таких как мосты, здания или краны. Анализ движения маятника позволяет предсказывать возможные деформации и динамические нагрузки на конструкции, что очень важно для обеспечения их безопасности и надежности.

Кроме того, уравнение математического маятника широко используется в контроле качества продукции, например, в автомобильной или авиационной промышленности. С помощью маятниковых испытаний можно определить прочность и долговечность различных материалов и конструкций, что помогает создавать более надежные и безопасные изделия.

Таким образом, уравнение движения маятника имеет множество практических применений в различных областях науки и техники. Знание этого уравнения позволяет эффективно проектировать, тестировать и улучшать различные механические системы, что является важным условием для развития инженерных наук и технологий в целом.

Какие еще уравнения используются для описания движения маятника?

Помимо уравнения математического маятника, существует ряд других уравнений, которые используются для описания движения маятника.

• Уравнение кругового маятника — описывает движение маятника, который движется по окружности. В данном случае уравнение зависит от угловой скорости маятника и его радиуса.
• Уравнение динамического маятника — учитывает не только гравитационную силу, но также и другие силы, действующие на маятник (например, силу вязкого трения). Это уравнение можно использовать для описания движения маятника в условиях, когда пренебрегать влиянием других сил нельзя.
• Уравнение волнового маятника — описывает движение маятника, который движется не только в одной плоскости, но и в трех измерениях. Это уравнение широко используется для описания движения жидкостей и газов.

Выбор уравнения зависит от конкретной задачи и условий, в которых происходит движение маятника. Но в любом случае, уравнения позволяют более точно описать движение маятника и прогнозировать его поведение в будущем.

Видео по теме:

Вопрос-ответ:

Что такое математический маятник?

Математический маятник — это идеализированная модель физического маятника, представляющая собой тяжелое тело, подвешенное на невесомой и нерастяжимой нити, движущееся с постоянной скоростью. Математический маятник дает возможность изучать уравнение движения маятника и его основные свойства.

Как записать уравнение движения математического маятника?

Уравнение движения математического маятника имеет вид: θ» + (g / l) * sin(θ) = 0, где θ — угол отклонения маятника от вертикали, l — длина нити, g — ускорение свободного падения. В этом уравнении θ» означает двойную производную функции θ по времени.

Какие свойства математического маятника изучают с помощью его уравнения движения?

Уравнение движения математического маятника позволяет изучать его период колебаний, зависимость периода от длины нити и ускорения свободного падения, амплитуду колебаний, скорость и ускорение маятника в каждый момент времени, а также форму и частоту колебания.

Как зависит период колебаний математического маятника от его длины?

Период колебаний математического маятника (время, за которое он совершает один полный цикл) зависит от длины нити и ускорения свободного падения, и может быть вычислен с помощью формулы Т = 2π√(l/g), где T — период колебаний, l — длина нити, g — ускорение свободного падения.

Как изменится период колебаний математического маятника при увеличении его амплитуды?

Период колебаний математического маятника не зависит от его амплитуды (максимального угла отклонения от вертикали), так как уравнение движения не содержит этого параметра. Однако, большая амплитуда может привести к изменению формы колебаний и увеличению их длительности.

Что произойдет с движением математического маятника, если он отклонить на угол более 90 градусов?

Если математический маятник отклонить на угол более 90 градусов, то он не будет колебаться вокруг вертикального положения равновесия, а начнет вращаться вокруг точки подвеса, совершая полный оборот. Этот тип движения называется вращательным или круговым движением.

Как уравнение движения математического маятника связано с другими уравнениями физической механики?

Уравнение движения математического маятника является дифференциальным уравнением второго порядка и имеет много общего с другими дифференциальными уравнениями физической механики, такими как уравнение гармонического осциллятора или уравнение пр ressure Laplace. Решение этого уравнения может быть получено с помощью различных методов, включая метод Фурье, метод Рунге-Кутты и метод конечных разностей.

Преимущества использования уравнения движения маятника

Уравнение движения математического маятника очень полезно для описания его движения. Оно позволяет установить зависимость между физическими параметрами маятника и его движением. Эта зависимость позволяет исследовать и предсказывать движение маятника.

Одним из преимуществ использования уравнения движения маятника является возможность определения периода колебаний. Период колебаний — это время, за которое маятник проходит полный цикл. Его можно найти по формуле, которая выводится из уравнения движения маятника.

Еще одно преимущество использования уравнения движения маятника — это возможность получения количественных оценок. Уравнение позволяет определить высоту подъема маятника, скорость его движения и другие параметры, которые могут быть непросто измерить экспериментально.

В целом, уравнение движения математического маятника является очень полезным инструментом для изучения его движения. Оно помогает проводить эксперименты в теоретической физике, а также находить практические применения в инженерных расчетах.

Недостатки использования уравнения математического маятника

Уравнение математического маятника используется для описания движения маятника втянутого на пружину. Однако, данное уравнение имеет некоторые недостатки, которые могут быть проблематичными в некоторых случаях.

Во-первых, уравнение математического маятника учитывает только движение маятника в одной плоскости, что не позволяет описать движения маятника в трехмерном пространстве. Это может быть особенно проблематичным для некоторых инженерных решений, где возможны трехмерные движения маятника.

Во-вторых, уравнение математического маятника не учитывает влияние внешних факторов, таких как сопротивление воздуха или трение. В реальных условиях, эти факторы могут замедлять или ускорять движение маятника, что может привести к неточности расчетов.

В-третьих, использование уравнения математического маятника может быть сложным для людей без математической подготовки. Для того чтобы использовать данное уравнение, требуется знание различных математических концепций, что может быть проблематичным для некоторых людей.

Использование уравнения математического маятника может иметь некоторые недостатки, однако, при правильном использовании данное уравнение может быть полезным инструментом для описания движения маятника и его свойств.