Что такое показатель в математике
Содержимое
- 1 Что такое показатель в математике
- 1.1 Что такое показатель в математике?
- 1.2 Видео по теме:
- 1.3 Определение и основные понятия
- 1.4 Как работать с показателями?
- 1.5 Примеры простых показателей
- 1.6 Как упростить показатель?
- 1.7 Примеры упрощения показателей
- 1.8 Показатели с отрицательными степенями
- 1.9 Примеры показателей с отрицательными степенями
- 1.10 Вопрос-ответ:
Показатель в математике — это число, которое указывает, сколько раз нужно умножить одно число (основание) на себя, чтобы получить другое число. В математическом выражении показатель обозначается как верхний индекс после основания и позволяет компактно записать множество повторяющихся умножений. Показатель имеет важное значение в различных областях математики, включая алгебру, геометрию и теорию вероятностей.
Показатель — важное понятие в математике, которое используется для обозначения степени числа. Он помогает нам выразить сколько раз нужно умножить число на себя, чтобы получить заданное значение. Показатель является значением, которое располагается в верхней части степени и указывает на количество умножений.
Для лучшего понимания показателя, рассмотрим пример. Пусть нам нужно вычислить значение 3 в степени 4. Здесь число 3 является основанием степени, а число 4 — показателем. Это означает, что нам нужно умножить число 3 на себя 4 раза: 3 * 3 * 3 * 3 = 81. Таким образом, 3 в степени 4 равно 81.
Показатель также может быть отрицательным числом или дробью. Например, если у нас есть 2 в степени -3, то это означает, что нам нужно взять обратное значение числа 2 и возвести его в степень 3: 1/(2*2*2) = 1/8. А если мы имеем 4 в степени 1/2, то это означает, что нам нужно взять квадратный корень из числа 4: √4 = 2.
В математике показатель находит широкое применение в различных областях, таких как физика, экономика, информатика и других. Он позволяет упрощать вычисления и делать их более компактными. Понимание показателя является основой для работы с различными математическими операциями и концепциями, поэтому его изучение является важным элементом математического образования.
Что такое показатель в математике?

Показатель состоит из двух частей: основания и показателя. Основание – это число или выражение, которое возводится в степень. Показатель – это число, которое показывает, сколько раз основание нужно умножить на себя.
Например, в выражении 2^3 основание равно 2, а показатель равен 3. Это означает, что число 2 нужно умножить на себя 3 раза: 2 * 2 * 2 = 8.
Показатели широко применяются в математике и науке для обозначения больших и маленьких чисел, а также для решения различных задач и уравнений. Они позволяют упростить запись и вычисления, делая их более удобными и понятными.
В математике существуют различные правила и свойства показателей, которые позволяют выполнять операции с ними, такие как умножение, деление, возведение в степень и извлечение корня. Знание и понимание этих свойств помогает решать сложные задачи и упрощать выражения.
Важно отметить, что показатель может быть как положительным, так и отрицательным, а также может быть дробным или даже иррациональным числом. Все это расширяет возможности использования показателей и делает их мощным инструментом в математике.
Видео по теме:
Определение и основные понятия
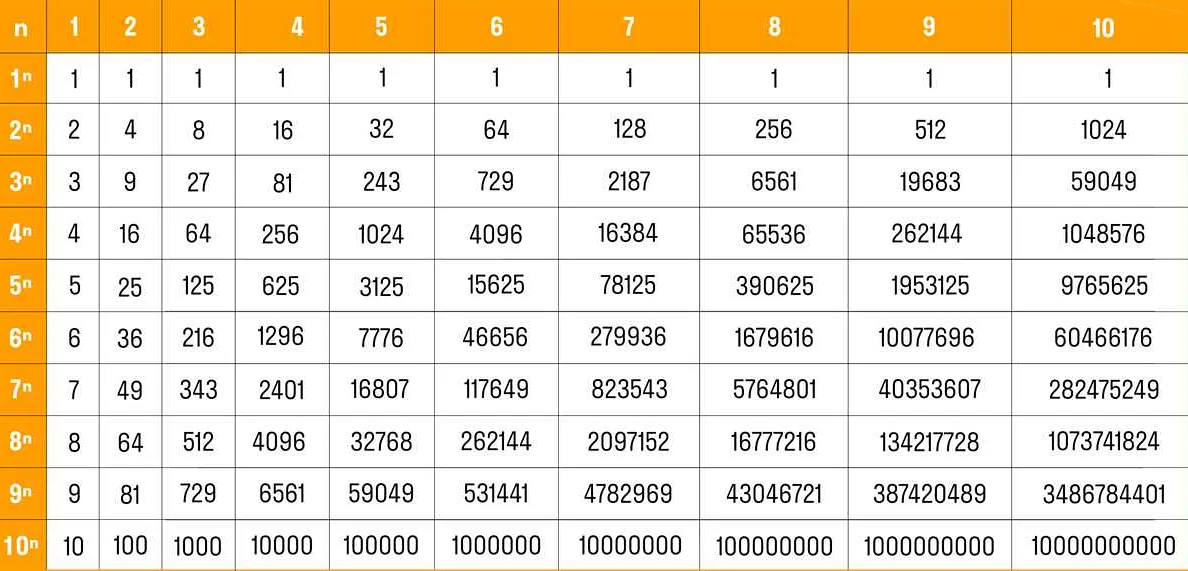
Основные понятия, связанные с показателем:
- Показатель: числовой показатель, указывающий на количество повторений основания в произведении.
- Основание: число, которое повторяется определенное количество раз в произведении.
- Произведение: результат умножения основания на себя столько раз, сколько указано в показателе.
Например, для показателя 3 и основания 2, произведение будет равно 2 * 2 * 2 = 8.
Показатель можно представить в виде дроби, где числитель указывает на количество повторений основания, а знаменатель — на количество повторений в знаменателе. Например, показатель 2/3 означает, что основание повторяется два раза в числителе и три раза в знаменателе.
Показатель имеет важные свойства и правила, которые позволяют выполнять различные операции с ним. Например, для показателей с одинаковым основанием выполняется правило умножения: a^m * a^n = a^(m+n), где a — основание, m и n — показатели.
Показатель также может быть отрицательным или дробным. В этих случаях применяются соответствующие правила для работы с ними.
Как работать с показателями?
Показатели в математике часто используются для описания и измерения различных явлений и характеристик. Для работы с показателями необходимо учитывать следующие важные моменты:
1. Определение показателя. Показатель является числовым выражением, которое показывает степень или порядок некоторого значения. Обычно показатель записывается в виде числа, возведенного в степень, например, 2^3.
2. Правила работы с показателями. Для упрощения работы с показателями существуют определенные правила, которые необходимо знать. Например, при умножении чисел с одинаковым основанием показатели складываются, например, 2^3 * 2^4 = 2^(3+4) = 2^7.
3. Примеры работы с показателями. Рассмотрим несколько примеров:
а) 5^2 / 5^3 = 1/5^(3-2) = 1/5^1 = 1/5.
б) (2^3)^4 = 2^(3*4) = 2^12.
в) (3^2 * 2^3)^2 = 3^(2*2) * 2^(3*2) = 3^4 * 2^6.
4. Задачи на работу с показателями. Для закрепления знаний по работе с показателями можно решать задачи, которые включают в себя операции с показателями. Например, найдите значение выражения 4^2 * 4^3.
Работа с показателями требует внимания и точности, но при достаточной практике становится более простой и понятной. Правильное использование показателей позволяет более эффективно работать с числами и выражениями в математике.
Примеры простых показателей
- Индекс роста: показатель, используемый для измерения темпов роста популяции. Он вычисляется как отношение числа людей в настоящий момент к числу людей в определенный прошлый момент времени и умножается на 100. Например, если на данный момент времени в городе проживает 200 тысяч человек, а двадцать лет назад их было 100 тысяч, то индекс роста будет равен 200%.
- Уровень безработицы: показатель, используемый для измерения процента безработных людей в определенной области или стране. Он вычисляется как отношение числа безработных к числу экономически активного населения и умножается на 100. Например, если в стране численность безработных равна 2 миллионам, а экономически активное население составляет 10 миллионов человек, то уровень безработицы будет равен 20%.
- Индекс инфляции: показатель, используемый для измерения уровня роста цен на товары и услуги в определенный период времени. Он вычисляется как отношение изменения индекса цен к исходному индексу и умножается на 100. Например, если индекс цен за прошлый год равен 120, а за текущий год 140, то индекс инфляции будет равен 16,67%.
Примеры простых показателей могут помочь понять, как они используются для анализа данных и принятия решений на основе числовых фактов. Они представляют собой удобные и эффективные инструменты для оценки различных аспектов реального мира.
Как упростить показатель?
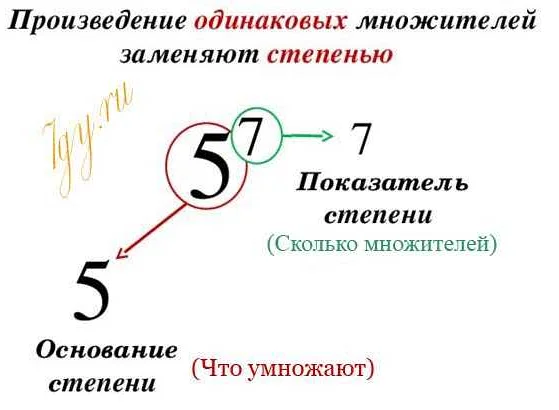
Для упрощения показателя можно использовать некоторые основные свойства показателей:
- Свойство умножения показателей: am * an = am+n. Это свойство позволяет складывать показатели, если основа показателя одинаковая.
- Свойство деления показателей: am / an = am-n. Это свойство позволяет вычитать показатели, если основа показателя одинаковая.
- Свойство возведения в степень показателя: (am)n = am*n. Это свойство позволяет умножать показатели, если основа показателя одинаковая.
- Свойство корня из показателя: √(am) = am/2. Это свойство позволяет делить показатель на 2, если основа показателя одинаковая.
Применение этих свойств позволяет значительно упростить выражения с показателями и сделать их более компактными и понятными.
Например, рассмотрим выражение 23 * 24. Используя свойство умножения показателей, мы можем сложить показатели и получить 27. Таким образом, мы упростили выражение и сократили его до более простого вида.
Упрощение показателя является важным навыком, который поможет вам более эффективно работать с показательными функциями и решать математические задачи.
Примеры упрощения показателей
Показатели могут быть упрощены с помощью различных правил.
Рассмотрим несколько примеров упрощения показателей:
1. 3/2 в степени 2 равно 32/22 = 9/4.
2. (23)4 = 23*4 = 212.
3. am * an = am+n. Например, a2 * a3 = a2+3 = a5.
4. (am)n = am*n. Например, (a2)3 = a2*3 = a6.
5. am / an = am-n. Например, a6 / a3 = a6-3 = a3.
Это только некоторые из множества возможных упрощений показателей. Правила упрощения показателей играют важную роль в алгебре и дальнейшем изучении математики.
Показатели с отрицательными степенями

В математике показатели с отрицательными степенями часто возникают при работе с десятичными дробями. Показатель с отрицательной степенью указывает, что число нужно возвести в обратную степень и полученный результат записывается в виде десятичной дроби.
Например, 2-3 означает, что число 2 нужно возвести в обратную третью степень. Обратная третья степень числа 2 равна 1/23 = 1/8 = 0,125.
Показатели с отрицательными степенями также могут быть представлены в виде дробей с положительными показателями. Например, 1/2-2 = (2/1)2 = 4/1 = 4.
Показатели с отрицательными степенями играют важную роль в научных и инженерных вычислениях, а также в экономике и финансах.
Примеры показателей с отрицательными степенями
Показатели с отрицательными степенями используются в математике для обозначения дробных значений. Они представляют собой обратные значения показателей с положительными степенями. Вот несколько примеров:
- 5-2 = 1/52 = 1/25 — показатель с отрицательной степенью обозначает взятие обратного значения квадрата числа 5.
- 10-3 = 1/103 = 1/1000 — показатель с отрицательной степенью означает взятие обратного значения куба числа 10.
- 2-4 = 1/24 = 1/16 — показатель с отрицательной степенью представляет обратное значение четвертой степени числа 2.
Таким образом, показатели с отрицательными степенями позволяют работать с дробными значениями и обозначать обратные значения положительных степеней чисел.
Вопрос-ответ:
Что такое показатель в математике?
Показатель в математике — это число, указывающее, сколько раз нужно умножить другое число на самого себя.
Как определить показатель числа?
Чтобы определить показатель числа, нужно посмотреть, сколько раз это число участвует в умножении.
Какие примеры можно привести для показателя числа?
Например, показатель числа 2 в степени 3 равен 8, потому что 2 умножается на само себя три раза (2 * 2 * 2 = 8).
Какой показатель у числа 10 в степени 0?
Показатель числа 10 в степени 0 равен 1. Это означает, что любое число, возведенное в нулевую степень, равно 1.
Можно ли использовать отрицательные показатели?
Да, можно использовать отрицательные показатели. Например, число 2 в степени -2 равно 1/4 (или 0,25), потому что 2 умножается на себя два раза с противоположным знаком (1/2 * 1/2 = 1/4).
Что такое показатель в математике?
Показатель в математике — это число, стоящее в верхней части степени и определяющее количество раз, которое нужно умножить число (основание) само на себя. Например, в выражении 2^3 число 2 называется основанием, а число 3 — показателем степени.

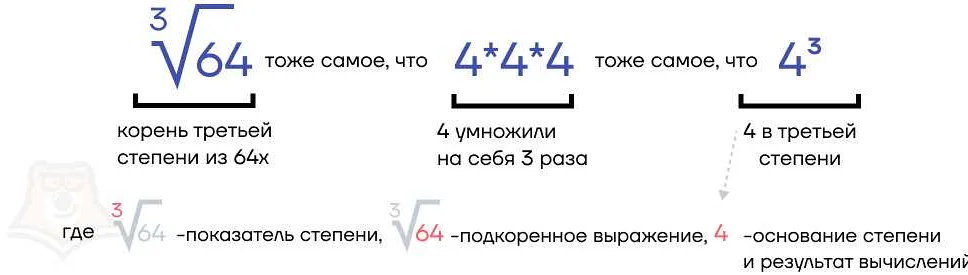
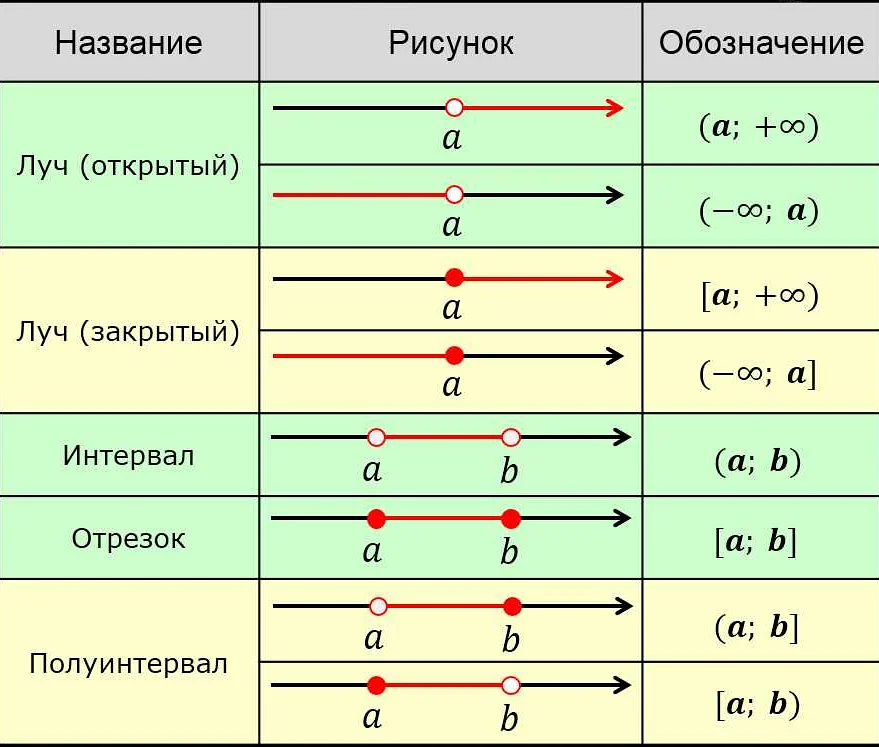
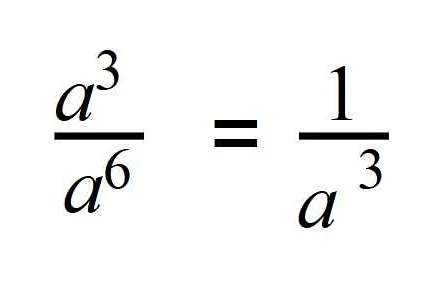

Статья очень понравилась! Очень ясно и доступно объясняется, что такое показатель в математике. Я раньше слышал об этом понятии, но никогда не мог понять, что оно означает. Теперь все стало понятно. Очень понравились примеры, которые были приведены в статье. Они помогли мне лучше усвоить материал и увидеть, как применять показатели на практике. Я считаю, что показатели являются очень важным инструментом в математике и заслуживают большего внимания со стороны учеников. Спасибо автору за такую информативную и полезную статью! Я уже не теряюсь, когда вижу показатель в математической задаче, а наоборот, с радостью приступаю к ее решению.
Математика — это наука, которую я всегда относила к сложным и непонятным. Однако, показатель — это понятие, которое я легко освоила благодаря данной статье. Показатель — это число, которое указывает, сколько раз нужно умножить другое число на себя. Например, показатель 2 в степени 3 означает, что число нужно умножить само на себя три раза: 2 × 2 × 2 = 8. Это очень полезное понятие, которое применяется во многих областях, включая физику, экономику и программирование. Я рада, что я теперь понимаю, что такое показатель и как его использовать. Статья была очень информативной и понятной для меня, и я рекомендую ее всем, кто хочет разобраться в этом понятии.