Что представляет собой модель математического маятника физика

Математический маятник — это модель, используемая физиками для изучения колебаний. Он представляет собой абстрактную систему, состоящую из точечной массы, подвешенной на идеальной нерастяжимой нити. Модель позволяет анализировать основные характеристики маятника, такие как период колебаний, амплитуда и зависимость от начальных условий. Математический маятник является одной из основных моделей, используемых для изучения колебаний в физике.

Математический маятник — это простая физическая система, которая состоит из массы, подвешенной на невесомой нерастяжимой нити или стержне. Одним из самых известных примеров такой системы является обычный маятник на часах. Математический маятник используется в науке и инженерии для изучения принципов колебательных движений и расчетов.

Основной принцип работы математического маятника заключается в том, что его колебания можно описать с помощью математической модели. В этой модели учитывается масса маятника, его длина и сила тяжести. Колебания маятника можно разделить на два типа: малые колебания и большие колебания. При малых колебаниях маятник совершает гармонические колебания, а при больших колебаниях возникают нелинейные эффекты.

Физические особенности математического маятника объясняются его уравнением движения. Оно выражает зависимость между ускорением маятника, его углом отклонения и другими факторами. Уравнение математического маятника является дифференциальным уравнением второго порядка и может быть решено аналитически или численно с использованием компьютерных программ.

Изучение модели математического маятника позволяет лучше понять принципы колебательных движений и их применение в различных областях науки и техники. Эта модель является одной из основных в физике и математике, и ее исследование помогает развивать навыки анализа и решения сложных задач. Кроме того, математический маятник является примером системы, которая может быть аппроксимирована с помощью линейных или нелинейных моделей, что делает его полезным инструментом в инженерии и технике.

Математический маятник: физические особенности и принцип работы

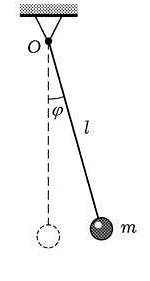
Физические особенности маятника определяются его конструкцией и параметрами. Основными параметрами являются длина подвеса и масса груза, а также амплитуда колебаний и начальная скорость. Длина подвеса определяет период колебаний маятника – время, за которое он совершает полный оборот. Масса груза влияет на инерцию системы и определяет силу, с которой маятник воздействует на свое окружение.

Принцип работы математического маятника основан на законе сохранения механической энергии. В начальный момент времени маятник отклоняют от равновесного положения на некоторый угол и отпускают. За счет силы тяжести маятник начинает двигаться, переходя из потенциальной энергии в кинетическую и обратно. При этом сумма потенциальной и кинетической энергии остается постоянной на протяжении всего движения.

Математический маятник является одной из фундаментальных моделей в физике и находит применение в различных областях науки и техники. Он используется для изучения колебаний и осцилляций, в теории управления и робототехнике, при расчете конструкций, связанных с маятниковым движением, а также в других областях, где требуется анализ и моделирование подобных систем.

ПараметрЗначение

Длина подвеса	Определяет период колебаний
Масса груза	Влияет на инерцию системы
Амплитуда колебаний	Задает максимальное отклонение маятника от равновесия
Начальная скорость	Определяет характер движения маятника при его отклонении

Видео по теме:

Начальное положение и движение маятника

Математический маятник представляет собой физическую систему, состоящую из невесомой нити (подвеса) и точечной массы, которая находится на конце нити. Начальное положение маятника определяется углом отклонения массы от вертикали. Движение маятника происходит под действием гравитационной силы, которая направлена вниз и стремится вернуть массу в исходное положение.

При малых углах отклонения движение маятника можно описать с помощью уравнения гармонического осциллятора. Уравнение маятника имеет вид:

θ(t)

=

A · cos(ωt + φ)

где:

• θ(t) — угол отклонения маятника в момент времени t;
• A — амплитуда колебаний маятника (максимальное отклонение от вертикали);
• ω — угловая скорость маятника;
• φ — начальная фаза колебаний маятника.

Зависимость угла от времени показывает, что маятник колеблется из стороны в сторону вокруг положения равновесия. При увеличении амплитуды колебаний, маятник будет описывать больший угол отклонения и пройдет больший путь. Угловая скорость маятника зависит от его длины, массы и величины гравитационного ускорения.

Начальное положение маятника и его движение являются основополагающими характеристиками для изучения его динамики и поведения в различных условиях. Точное моделирование начального положения и движения маятника позволяет предсказывать его дальнейшее поведение и применять в различных областях науки и техники.

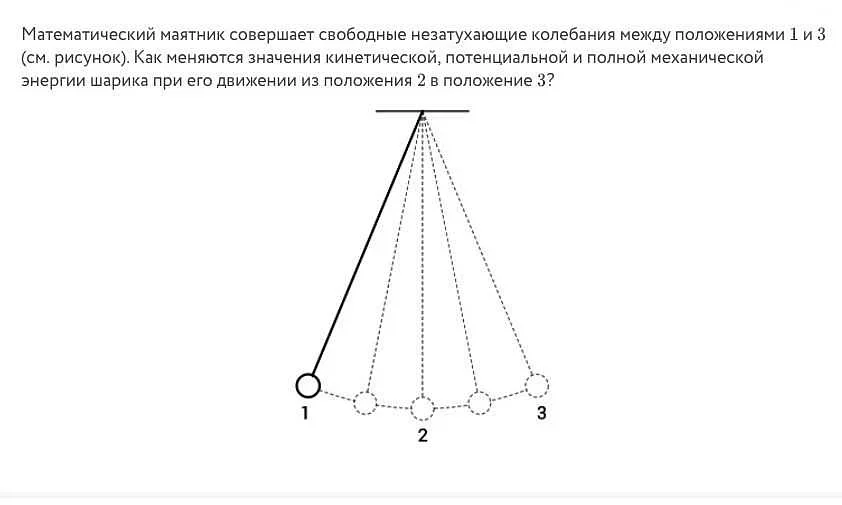
Закон сохранения энергии в системе

В системе математического маятника существует закон сохранения энергии, который гласит: сумма кинетической и потенциальной энергий остается постоянной.

Кинетическая энергия математического маятника определяется его скоростью и массой. Чем выше скорость и масса, тем больше кинетическая энергия.

Потенциальная энергия математического маятника зависит от его высоты и потенциальной энергии. Чем выше высота и потенциальная энергия, тем больше потенциальная энергия.

Когда математический маятник движется, его кинетическая энергия увеличивается, а потенциальная энергия уменьшается. Однако сумма этих энергий остается постоянной.

Закон сохранения энергии является фундаментальным принципом в физике и применим в различных системах, включая математический маятник. Этот закон помогает понять и объяснить поведение системы и ее энергетические характеристики.

Вопрос-ответ:

Как работает математический маятник?

Математический маятник представляет собой модель, которая используется для изучения колебаний. Он состоит из точечной массы, называемой маятником, подвешенной на невесомой нити или стержне. Когда маятник отклоняется от равновесной позиции и отпускается, он начинает колебаться вокруг этой позиции. Колебания математического маятника описываются математическими уравнениями, которые учитывают массу маятника, его длину, силу тяжести и силы сопротивления воздуха.

Какие физические особенности математического маятника важны для его работы?

Основными физическими особенностями математического маятника являются его масса, длина нити или стержня, а также сила тяжести и сила сопротивления воздуха. Масса маятника определяет его инерцию, а длина нити или стержня влияет на период колебаний. Сила тяжести действует на маятник, стремясь вернуть его в равновесное положение, а сила сопротивления воздуха замедляет его движение и уменьшает амплитуду колебаний.

Каков принцип работы математического маятника?

Принцип работы математического маятника основан на законах динамики и энергии. Когда маятник отклоняется от равновесной позиции, на него действуют сила тяжести и сила натяжения нити или стержня. Силы создают моменты относительно точки подвеса, вызывая ускорение маятника. При отклонении маятника энергия потенциальная превращается в энергию кинетическую и обратно, что обеспечивает его колебания вокруг равновесной позиции.

Можно ли применить модель математического маятника для описания реальных физических систем?

Модель математического маятника является упрощенной моделью и может быть использована для описания ряда реальных физических систем. Например, она может быть применена для изучения колебаний маятников в физических часах, маятниковых мостов, акселерометров и других устройств. Однако, для более точного описания сложных систем могут потребоваться более сложные модели и уравнения.

Каков принцип работы модели математического маятника?

Модель математического маятника работает на основе законов механики и физики. Она представляет из себя математическую абстракцию реального маятника, который колеблется вокруг некоторой точки под воздействием силы тяжести. В модели учитываются масса маятника, длина подвеса и угол отклонения от вертикали. При помощи уравнений движения и законов сохранения энергии и момента импульса можно определить поведение системы и прогнозировать колебания маятника.

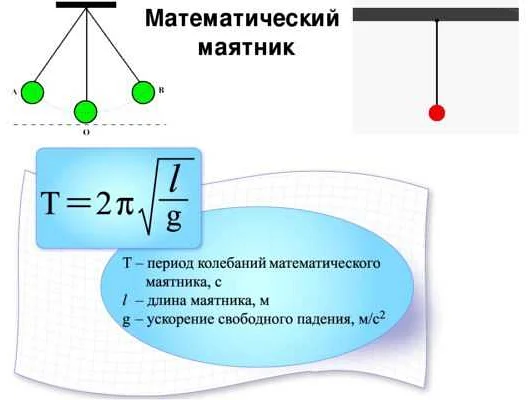
Зависимость периода колебаний от длины маятника

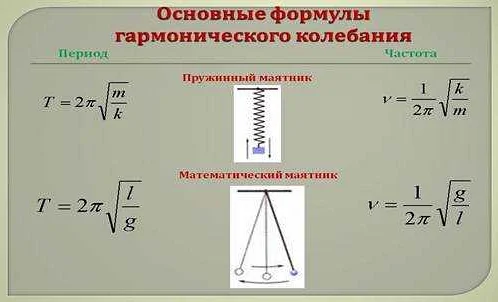
Оказывается, что период колебаний математического маятника пропорционален квадратному корню из длины нити маятника. Формула для расчета периода колебаний дана по формуле:

T = 2π * √(l / g)

где T — период колебаний (время, за которое маятник совершает полный цикл), l — длина нити маятника и g — ускорение свободного падения.

Из этой формулы видно, что с увеличением длины нити маятника, период колебаний также увеличивается. Это означает, что маятники с более длинными нитями будут колебаться медленнее, чем маятники с более короткими нитями.

Например, если у нас есть два математических маятника с длинами нитей в отношении 1:2, то период колебаний второго маятника будет в два раза больше, чем у первого маятника.

Зависимость периода колебаний от длины маятника имеет важное практическое значение. Она позволяет ученым и инженерам оптимизировать длину нити маятника для конкретных задач. Например, в часах с маятником длина нити выбирается таким образом, чтобы период колебаний соответствовал одной секунде.

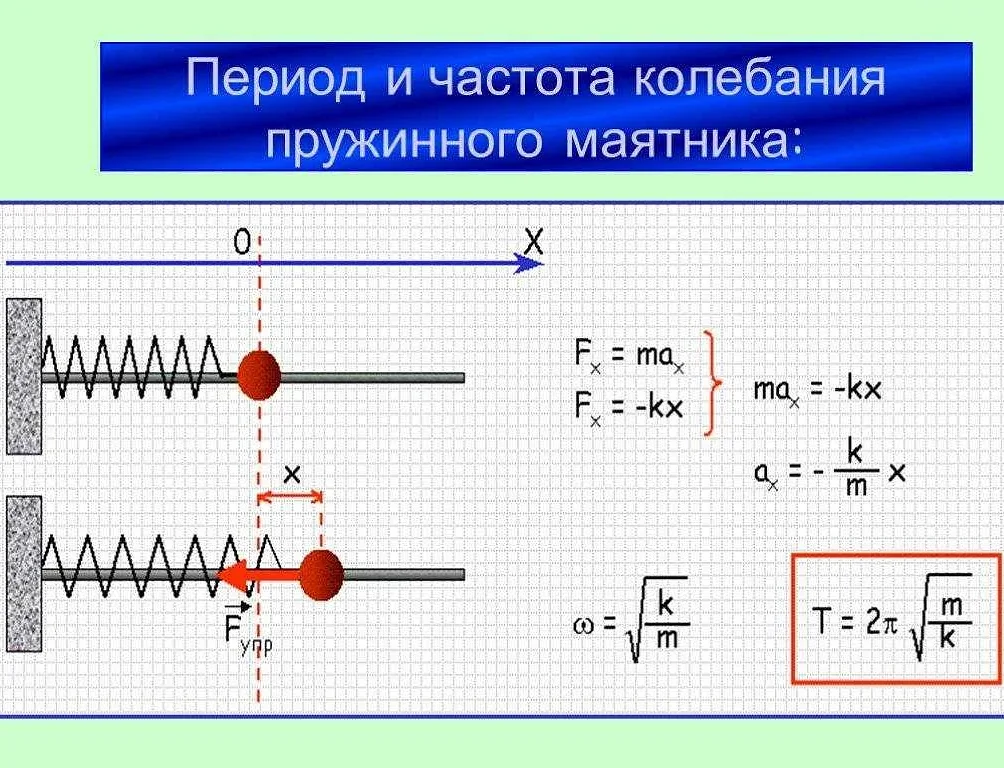
Влияние массы маятника на его движение

Это объясняется основными законами физики. Согласно закону инерции, масса объекта определяет его сопротивление изменению скорости. Чем больше масса маятника, тем больше его инерция, и тем сложнее его ускорить или замедлить.

Кроме того, масса маятника также влияет на его период колебаний. Период колебаний — это время, за которое маятник совершает одно полное колебание. Согласно формуле периода колебаний маятника, период прямо пропорционален квадратному корню из длины маятника и обратно пропорционален квадратному корню из ускорения свободного падения и массы маятника.

Таким образом, увеличение массы маятника приведет к увеличению его периода колебаний. Это означает, что масса маятника определяет скорость его движения и время, за которое он совершает колебания.

Демпфирование колебаний маятника

Существует два основных типа демпфирования: вязкое и сухое. Вязкое демпфирование связано с наличием вязкой среды, в которой маятник колеблется. Вязкая среда создает сопротивление движению маятника, что приводит к его затуханию. Сухое демпфирование происходит из-за трения между движущимися частями маятника, например, между осью и подшипниками.

Демпфирование колебаний маятника может оказывать влияние на его период колебаний и амплитуду. Вязкое демпфирование приводит к уменьшению амплитуды колебаний, а сухое демпфирование может привести к изменению периода колебаний.

Для математической модели маятника демпфирование учитывается путем добавления демпфирующей силы в уравнение движения. Эта сила пропорциональна скорости маятника и обратно пропорциональна его массе. Уравнение движения с учетом демпфирования можно записать в виде:

m · x» + c · x’ + k · x = 0

где m — масса маятника, x — смещение маятника от положения равновесия, c — коэффициент демпфирования, k — коэффициент жесткости.

В зависимости от значений коэффициента демпфирования и жесткости, маятник может проявлять различные типы колебаний: незатухающие, затухающие и переходные. Демпфирование является важным аспектом при изучении и моделировании математического маятника, так как оно определяет его динамические свойства и поведение во время колебаний.

Математическая модель маятника

Математическая модель маятника учитывает несколько физических особенностей этой системы. Во-первых, она учитывает гравитацию, которая оказывает влияние на движение маятника. Во-вторых, модель учитывает закон сохранения энергии, который позволяет определить скорость и положение маятника в любой момент времени. В-третьих, модель учитывает трение, которое оказывает влияние на затухание колебаний маятника.

Математическая модель маятника представляет собой дифференциальное уравнение, которое описывает движение маятника в зависимости от начальных условий и внешних сил. Это уравнение может быть решено численными методами, что позволяет получить точные значения скорости и положения маятника в любой момент времени.

Математическая модель маятника широко применяется в физике, инженерии и других науках для предсказания и изучения движения маятника. Она позволяет проводить различные эксперименты и анализировать поведение маятника в различных условиях. Также модель позволяет оптимизировать конструкцию маятников и предсказывать их работу в реальных условиях.

Таким образом, математическая модель маятника является мощным инструментом для изучения и предсказания поведения маятника. Она позволяет ученым и инженерам проводить различные исследования и оптимизировать работу маятников в различных областях науки и техники.

Решение уравнений движения маятника

Уравнение движения математического маятника выглядит следующим образом:

l · θ» + g · sin(θ) = 0

где l — длина маятника, θ — угол отклонения маятника, g — ускорение свободного падения.

Решение этого уравнения является нетривиальной задачей и обычно требует использования численных методов или приближенных аналитических решений. Однако, для небольших углов отклонения (θ < 15°) можно применить приближение малых углов (малое угловое приближение), которое упрощает уравнение и позволяет получить аналитическое решение.

В случае малых углов отклонения уравнение движения маятника можно аппроксимировать следующим образом:

l · θ» + g · θ = 0

Это уравнение является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Решение этого уравнения имеет вид:

θ(t) = A · cos(ωt + φ)

где A — амплитуда колебаний, ω — угловая частота, φ — начальная фаза.

Таким образом, решение уравнений движения математического маятника зависит от начальных условий (амплитуды, начальной фазы) и длины маятника.

Решение уравнений движения маятника является важным этапом при исследовании его характеристик и поведения. Оно позволяет предсказать, как будет изменяться угол отклонения маятника во времени и определить его период колебаний.

Применение математического маятника в научных и технических задачах

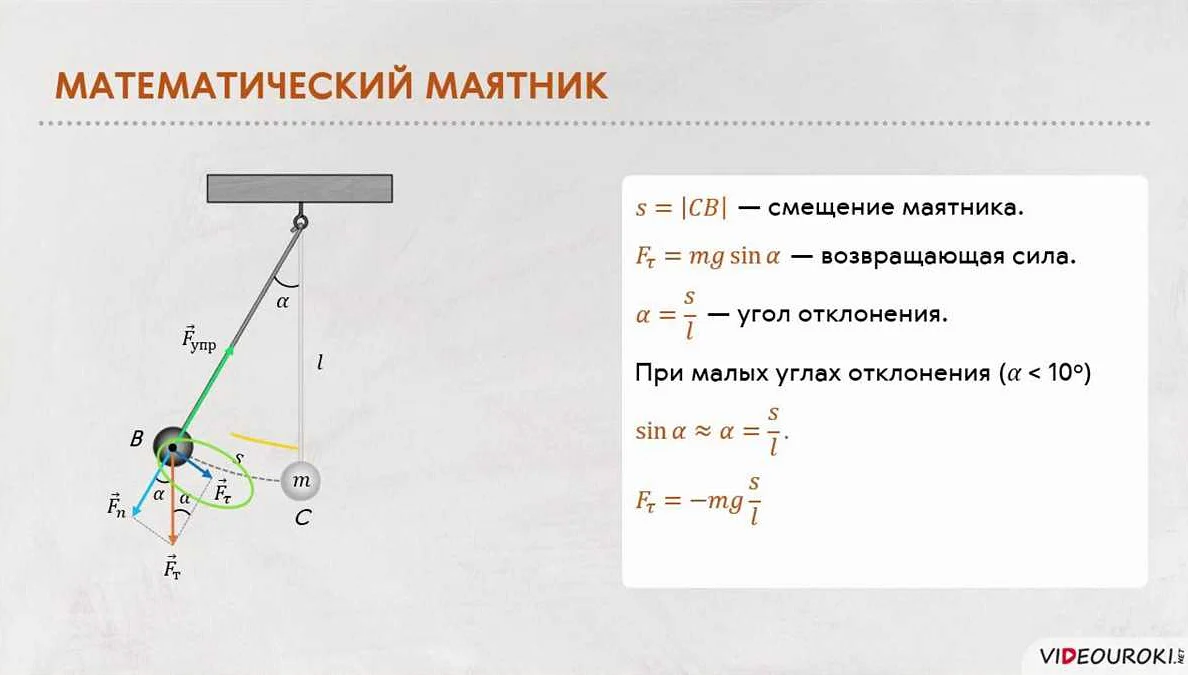
Математический маятник, являясь одной из простейших и наиболее изученных физических моделей, находит широкое применение в различных научных и технических задачах. Его простота и точность позволяют использовать эту модель для анализа различных явлений и процессов.

Одной из основных областей применения математического маятника является физика. Используя модель математического маятника, ученые и инженеры могут изучать и анализировать колебательные и осцилляционные процессы. Математический маятник позволяет исследовать различные параметры колебаний, такие как период колебаний, амплитуда и фаза. Это позволяет более глубоко понять и предсказать поведение систем, где присутствуют колебания, например, в механических или электрических системах.

Математический маятник также активно применяется в области математики. Использование этой модели позволяет изучать и решать различные задачи, связанные с колебаниями и гармоническими функциями. Многие математические методы и теоремы основаны на анализе колебательных систем, которые можно представить в виде математического маятника.

Кроме того, математический маятник находит применение в различных технических задачах. Например, он используется для измерения гравитационного ускорения или определения точного положения объекта в пространстве. Также математический маятник может быть использован при проектировании и расчете механизмов, основанных на колебаниях. Например, при разработке часов или других устройств, которые работают на основе колебательных движений.

В целом, применение математического маятника в научных и технических задачах позволяет более глубоко изучать и понимать различные физические и математические явления. Эта простая модель является мощным инструментом для анализа и предсказания поведения систем, где присутствуют колебания и осцилляции.