Что такое принцип дирихле в математике
Содержимое
- 1 Что такое принцип дирихле в математике
Принцип дирихле – это один из основных принципов комбинаторики и теории вероятностей, который в математике используется для решения задач на размещение объектов. Узнайте, как применить принцип дирихле для решения сложных математических задач.
Принцип Дирихле – это одна из фундаментальных концепций в математике, которая играет важную роль в различных областях, включая комбинаторику, теорию чисел и анализ. Этот принцип был впервые сформулирован немецким математиком Густавом Лебяриусом Дирихле в начале 19 века.
Принцип Дирихле утверждает, что если n + 1 объектов размещены в n контейнерах, то хотя бы в одном контейнере будет находиться не менее двух объектов. Простыми словами, если нарисовать n точек на плоскости и соединить их n-1 линиями, то хотя бы одна линия будет соединять две точки. Это простое утверждение может показаться очевидным, но его роль в математике невероятно важна.
Принцип Дирихле имеет широкое применение в комбинаторике и теории чисел. Он используется для доказательства различных теорем, включая теорему о делимости, принцип Дирихле для арифметических прогрессий и теорему Рамсея.
Принцип Дирихле также находит применение в других областях, таких как информатика и теория графов. Он помогает нам понять и решить проблемы связанные с распределением или выбором объектов. Другими словами, принцип Дирихле позволяет нам найти некую структуру, даже если изначально объекты кажутся случайно разбросанными.
В заключение, принцип Дирихле является фундаментальным инструментом в математике, который имеет широкое применение и помогает нам понять и решать различные задачи. Он позволяет нам обнаружить закономерности и структуры в сложных системах, и его понимание является важным для развития нашего понимания математики и ее приложений.
Что такое принцип Дирихле?
Принцип Дирихле утверждает, что если распределить n+1 объектов в n ящиках, то хотя бы в одном из ящиков окажется более одного объекта. Другими словами, если n+1 элементов разделить на n групп, то хотя бы в одной из групп будет не менее двух элементов.
Этот принцип находит широкое применение в различных областях математики, таких как теория чисел, комбинаторика, теория вероятностей и дискретная математика.
Принцип Дирихле является основой для доказательства многих теорем и утверждений. Он позволяет найти решения задач, связанных с распределением объектов по различным группам или ящикам. Например, применение принципа Дирихле позволяет доказывать существование и единственность решений уравнений, находить комбинаторные сочетания и строить оптимальные расписания.
Принцип Дирихле также играет важную роль в решении задач о неравенствах и оценках. Он позволяет устанавливать верхние и нижние границы для различных математических объектов и функций.
В заключение можно сказать, что принцип Дирихле является одним из фундаментальных принципов в математике, который широко используется для решения различных задач и доказательства теорем.
История открытия

Принцип Дирихле, также известный как принцип ящика или принцип Дирихле-Штольца, был впервые сформулирован немецким математиком Густавом Леопольдом Дирихле в 1834 году. Он был одним из величайших математиков своего времени и считается одним из основателей современной теории чисел.
Идея принципа Дирихле возникла в результате его исследований в области арфметических прогрессий и деления чисел. Дирихле задался вопросом о том, сколько элементов можно выбрать из некоторых множеств так, чтобы обязательно были выбраны элементы, удовлетворяющие определенным условиям.
Принцип Дирихле утверждает, что если имеется n+1 объектов, которые нужно разместить в n контейнерах, то как минимум в одном контейнере будет находиться не менее двух объектов. Другими словами, если количество объектов больше, чем количество контейнеров, то хотя бы в одном контейнере будет два и более объекта.
Этот принцип имеет широкое применение в различных областях математики, включая комбинаторику, теорию графов и теорию чисел. Он позволяет решать задачи, связанные с выбором и распределением элементов, а также находить ограничения и связи между различными множествами.
История и применение принципа Дирихле продолжается и в наше время, и он остается важным инструментом для изучения и решения различных математических проблем.
Объяснение принципа Дирихле

Принцип Дирихле утверждает, что если разместить несколько объектов в большем количестве контейнеров, чем количество объектов, то как минимум один контейнер должен содержать более одного объекта.
Другими словами, если у нас есть n объектов и m контейнеров, где n > m, то хотя бы один контейнер должен содержать более одного объекта.
Принцип Дирихле широко применяется в различных областях математики, включая комбинаторику, теорию чисел, графовую теорию и дискретную математику. Он предоставляет инструмент для поиска и доказательства существования объектов в различных задачах, основанных на сочетаниях и перестановках.
Применение принципа Дирихле может помочь в решении различных задач, например, для доказательства существования двух людей, имеющих ровно одинаковое количество волос, или нахождения двух одинаковых чисел в заданном множестве.
Принцип Дирихле является основой для ряда других математических принципов и теорем, и его понимание является важным для изучения и применения различных областей математики.
Математическая формулировка
Более формально, пусть A и B – два множества, причём A ⊂ B. Если мощность множества A бесконечна, а мощность множества B конечна или счётна, то множество B содержит бесконечное количество элементов из множества A.
Данный принцип находит широкое применение в различных областях математики, включая анализ, комбинаторику, теорию чисел и математическую логику. Он помогает доказывать существование бесконечных последовательностей, решать задачи на существование объектов с определенными свойствами и исследовать различные математические структуры.
Интуитивное понимание
Наиболее простым примером для интуитивного понимания принципа Дирихле является ситуация, когда в комнате находятся больше людей, чем имеется стульев. В таком случае, по крайней мере одному человеку придется стоять. Аналогично, если в некотором множестве имеется больше элементов, чем в другом множестве, то будет существовать хотя бы одно соответствие нескольким элементам первого множества.
Принцип Дирихле находит широкое применение в различных областях математики, таких как комбинаторика, анализ алгоритмов, теория чисел и др. Он помогает установить взаимосвязи между структурами и определить существование определенных свойств.
Применение принципа Дирихле

Принцип Дирихле имеет широкое применение в различных областях математики. Он позволяет решать разнообразные задачи, связанные с расстановкой и размещением объектов.
Одним из основных применений принципа Дирихле является задача о размещении шаров в ящиках. Известно, что если количество шаров больше, чем количество ящиков, то как минимум один из ящиков будет содержать более одного шара. Это следует из принципа Дирихле, поскольку в данном случае количество шаров превышает количество ящиков, и, следовательно, хотя бы в одном ящике должно быть не менее двух шаров.
Еще одним примером применения принципа Дирихле является задача о расстановке гостей на свадьбе. Если количество гостей больше, чем количество мест за столом, то как минимум два гостя будут сидеть рядом. Это объясняется принципом Дирихле, так как количество гостей превышает количество мест за столом, и, следовательно, хотя бы два гостя должны занять одно и то же место.
Принцип Дирихле также применяется в комбинаторике и теории вероятностей. Например, при решении задач о различных комбинациях элементов или о повторении событий.
Таким образом, принцип Дирихле является важным инструментом для решения задач, связанных с расстановкой, размещением и комбинированием объектов. Он позволяет находить общие закономерности и решать задачи, основываясь на простых принципах и логике.
Теория чисел

Одной из основных задач теории чисел является разложение целых чисел на простые множители. Это позволяет представить любое целое число в виде произведения простых чисел и упростить решение других задач, связанных с целыми числами.
Еще одной важной задачей теории чисел является изучение делимости. Теорема о делении с остатком позволяет определить, делится ли одно число на другое без остатка, а теорема Евклида позволяет найти наибольший общий делитель двух чисел.
Теория чисел имеет множество применений в других областях математики, таких как криптография, теория кодирования и алгоритмы. Она также имеет связь с другими областями математики, такими как комбинаторика, алгебра и анализ.
Комбинаторика

Основные понятия комбинаторики включают в себя:
- Перестановки – упорядоченные анаграммы элементов множества. Количество перестановок вычисляется как n!, где n – количество элементов.
- Сочетания – неупорядоченные выборки элементов множества. Количество сочетаний определяется формулой С(n, k) = n! / (k!(n — k)!), где n – количество элементов, а k – количество выбранных элементов.
- Размещения – упорядоченные выборки элементов множества. Количество размещений определяется формулой A(n, k) = n! / (n — k)!, где n – количество элементов, а k – количество выбранных элементов.
Комбинаторика помогает решать задачи, связанные с подсчетом возможных вариантов и установлением вероятностей различных событий. Она также применяется для оптимизации алгоритмов, разработки эффективных кодов исправления ошибок, создания криптографических систем и многое другое.
Математическая физика
Математическая физика играет важную роль в различных областях науки и техники, включая механику, электродинамику, квантовую физику и термодинамику. Она помогает установить законы и принципы, которые описывают природу и позволяют предсказывать поведение физических систем.
Принципы математической физики, такие как принцип Дирихле, часто используются для решения сложных задач. Принцип Дирихле, сформулированный немецким математиком Петером Густавом Лейпцигским в 19 веке, утверждает, что если границы области заданы, то решение дифференциального уравнения внутри этой области единственно.
Применение математической физики в реальных задачах позволяет нам более глубоко понять природу окружающего нас мира. Она играет важную роль в разработке новых технологий и улучшении существующих. Благодаря математической физике мы можем моделировать и прогнозировать поведение сложных систем, таких как погода, гравитационные поля и квантовые физические явления.
Теория графов

В теории графов рассматриваются различные типы графов, такие как ориентированные и неориентированные, взвешенные и невзвешенные, связные и несвязные графы. Кроме того, важным понятием является понятие пути в графе, которое описывает последовательность вершин и ребер, соединяющих их.
Теория графов находит применение в различных областях, таких как транспортная логистика, компьютерные сети, социальные сети, теория игр и многих других. Она позволяет решать задачи оптимизации, моделирования и анализа сложных систем.
Для представления и анализа графов применяются различные методы и алгоритмы. Например, алгоритмы поиска кратчайшего пути, алгоритмы поиска минимального остовного дерева, алгоритмы центральности вершин и др. Также существуют различные показатели и метрики, которые используются для оценки свойств и характеристик графов.
Теория графов имеет множество применений и является неотъемлемой частью современной математики. Она позволяет анализировать и понимать сложные взаимосвязи и структуры, которые существуют в различных системах и явлениях.
Тип графаОписание
| Ориентированный граф | Граф, в котором каждое ребро имеет направление |
| Неориентированный граф | Граф, в котором каждое ребро не имеет направления |
| Взвешенный граф | Граф, в котором каждому ребру присвоено числовое значение |
| Невзвешенный граф | Граф, в котором каждому ребру не присвоено числовое значение |
| Связный граф | Граф, в котором между любыми двумя вершинами существует путь |
| Несвязный граф | Граф, в котором существуют вершины, не соединенные путем |
Видео по теме:
Что такое принцип Дирихле?
Принцип Дирихле — это основной принцип комбинаторики, который гласит, что если на n+1 объекте находится хотя бы n объектов и каждый из них может находиться на объекте только один раз, то хотя бы один объект будет не заполнен.
Как применяется принцип Дирихле в математике?
Принцип Дирихле находит широкое применение в различных областях математики, таких как комбинаторика, алгебра, теория чисел и анализ. Он используется для доказательства существования решений уравнений, построения графов, доказательства теорем, а также для решения задач на размещение и сочетание объектов.
Можете привести пример использования принципа Дирихле?
Конечно! Допустим, у нас есть 6 человек и мы хотим выбрать 5 из них для создания команды. Если каждый человек может быть только в одной команде, то по принципу Дирихле мы можем утверждать, что хотя бы два человека попадут в одну и ту же команду.
Каким образом принцип Дирихле связан с проблемой шляп и перчаток?
Проблема шляп и перчаток — это классическая задача, которая может быть решена с помощью принципа Дирихле. Представим, что у нас есть n пар шляп и n перчаток, которые были случайным образом перемешаны. Если n+1 человек будет выбирать по одной шляпе и перчатке, то по принципу Дирихле как минимум у одного человека окажутся совпадающие шляпа и перчатка.
Что такое принцип Дирихле?
Принцип Дирихле — это базовое математическое утверждение, которое гласит, что если на плоскости разбитой на области есть больше точек, чем областей, то хотя бы в одной области будет более одной точки.




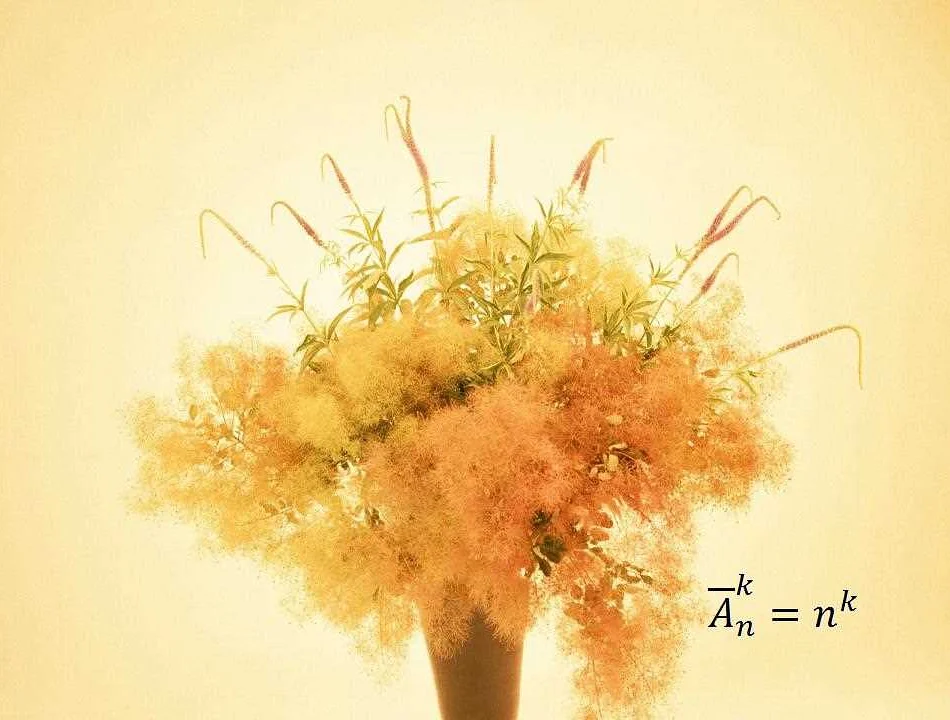
Статья очень понравилась! Принцип Дирихле – это очень интересный и важный математический принцип, который на первый взгляд может показаться сложным, но статья объясняет его достаточно простым и понятным языком. Я не математик, но благодаря этому тексту я смог понять суть принципа и его применение. Очень впечатляет пример с покрашенными точками на плоскости. Мне было интересно узнать, что если мы возьмем квадрат на плоскости, и случайным образом разместим на нем 5 точек, то обязательно найдутся две точки, расстояние между которыми будет меньше, чем длина стороны квадрата. Это просто потрясающе! Причем этот принцип применим не только к плоскости, но и к другим задачам, связанным с различными структурами. Теперь, когда я понял суть принципа Дирихле, мне стало понятно, как его можно использовать в решении различных задач. Это дает возможность найти определенные свойства или закономерности в различных математических структурах. Это может быть полезно во многих областях, таких как теория чисел, комбинаторика, графы и многое другое. Очень интересно, что принцип Дирихле можно применять не только в математике, но и в других науках, таких как физика и информатика. Это показывает его универсальность и важность. Я бы хотел узнать больше примеров применения принципа Дирихле в реальной жизни и в других областях науки. В целом, статья очень понятная и интересная. Я получил много новых знаний о принципе Дирихле и его применении в математике. Спасибо автору за такой информативный и увлекательный материал! Я надеюсь, что в будущем будут еще статьи на подобные темы.