Кратное что такое в математике
Содержимое
- 1 Кратное что такое в математике
- 1.1 Что такое кратное в математике?
- 1.2 Кратное числа: основная информация
- 1.3 Как определить, является ли число кратным?
- 1.4 Правила определения кратного числа
- 1.5 Кратность числа: примеры из жизни
- 1.6 Интересные факты о кратных числах
- 1.7 Кратное числа: практическое применение
- 1.8 Кратные числа и разложение на множители
- 1.9 Вопрос-ответ:
- 1.9.0.1 Что такое кратное числа?
- 1.9.0.2 Как определить, является ли число кратным другому числу?
- 1.9.0.3 Как найти все кратные числа для заданного числа?
- 1.9.0.4 Может ли число быть кратным самому себе?
- 1.9.0.5 Какие свойства имеют кратные числа?
- 1.9.0.6 Что такое кратное в математике?
- 1.9.0.7 Как определить, является ли число кратным другому числу?
- 1.10 Видео по теме:
Кратное в математике — это число, которое делится на другое число без остатка. Узнайте, как определить кратность числа и как использовать это понятие в различных математических задачах.
Математика – это наука, изучающая числа, их свойства и взаимоотношения. Одно из важных понятий в математике – кратное. Кратное числа – это число, которое делится на данное число без остатка.
Например, число 10 является кратным числу 5, так как 10 делится на 5 без остатка. В то же время, число 10 не является кратным числу 3, так как 10 делится на 3 с остатком.
Кратное число можно определить с помощью деления. Если при делении данного числа на данное число результат равен нулю, то число является кратным. Например, чтобы определить, является ли число 24 кратным числу 8, нужно разделить 24 на 8. Если результат деления равен нулю, то число 24 является кратным числу 8.
Кратные числа широко используются в математике и других научных областях. Например, кратность часто применяется в алгебре, где кратные числа используются для решения уравнений и систем уравнений.
Таким образом, кратное – это число, которое делится на данное число без остатка. Определить кратность числа можно с помощью деления, если результат деления равен нулю, то число является кратным.
Что такое кратное в математике?
В математике кратным числу называется число, которое делится на данное число без остатка. Если число a делится на число b без остатка, то число a называется кратным числу b.
Например, число 10 является кратным числу 5, потому что оно делится на 5 без остатка. А число 15 является кратным числу 3, так как оно также делится на 3 без остатка.
Чтобы определить, является ли число кратным другому числу, нужно проверить, делится ли оно на это число без остатка. Если при делении числа a на число b остаток равен нулю, то число a является кратным числу b.
Если число a не делится на число b без остатка, то число a не является кратным числу b. Например, число 7 не является кратным числу 4, так как при делении 7 на 4 остаток будет равен 3.
Кратность чисел часто используется в различных областях, например, в арифметике, алгебре, геометрии, физике и т. д. Знание понятия «кратное» позволяет более точно описывать и решать различные задачи и проблемы, связанные с числами и их свойствами.
Кратное числа: основная информация
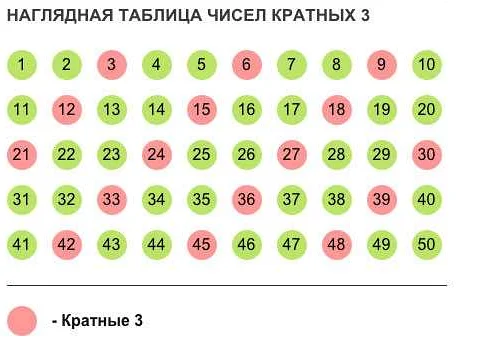
Кратным числом называется число, которое делится на другое число без остатка. В математике кратность определяется отношением деления числа на другое число.
Для определения кратности числа A числу B, необходимо проверить, равен ли остаток от деления A на B нулю. Если остаток равен нулю, то число A является кратным числу B.
Например, число 12 является кратным числам 2 и 3, так как оно без остатка делится на эти числа: 12 ÷ 2 = 6 и 12 ÷ 3 = 4.
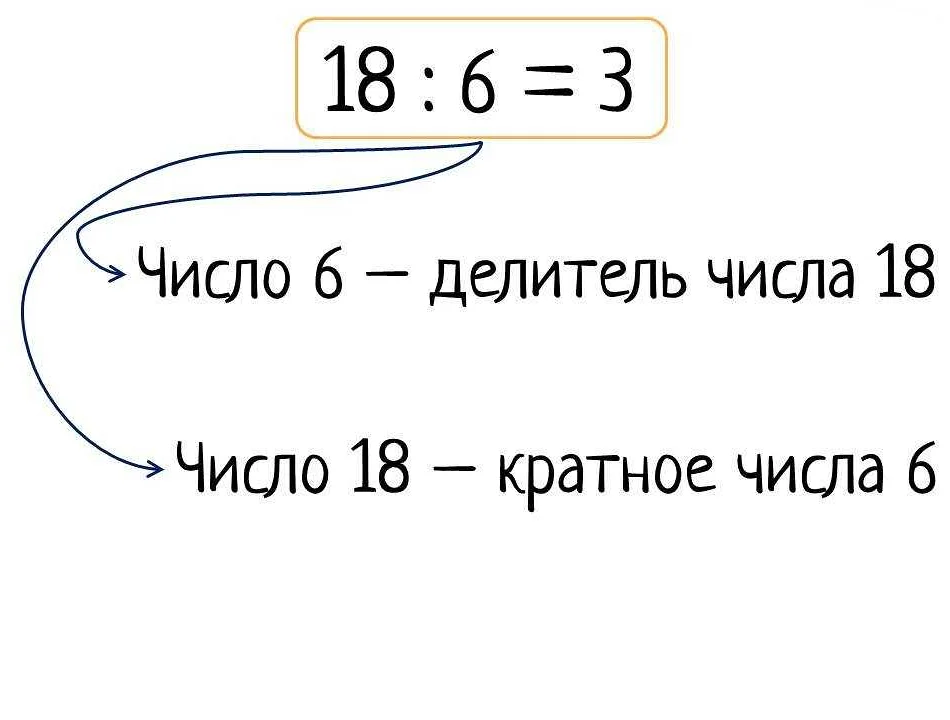
Число, на которое делится другое число, называется делителем или множителем. Например, в примере выше число 2 и 3 являются делителями числа 12.
Кратные числа играют важную роль в математике и широко используются в различных задачах и приложениях. Они помогают упростить вычисления, а также находят применение в алгебре, геометрии, физике, экономике и других областях.
Как определить, является ли число кратным?
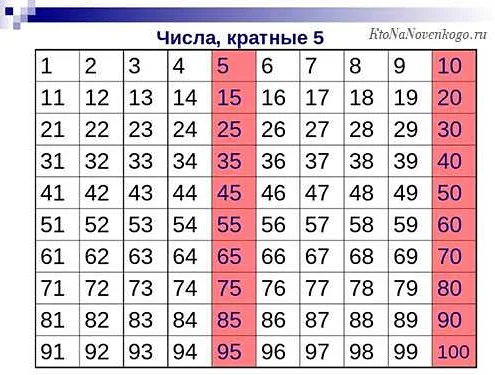
Например, для проверки, является ли число 12 кратным числу 4, необходимо разделить 12 на 4. Если при делении получится остаток равный нулю, то число 12 является кратным 4.
Для определения кратности числа также можно использовать следующий признак: число является кратным другому числу, если оно делится на это число без остатка. Например, число 20 кратно 5, так как 20 делится на 5 без остатка.
Кратность числа можно проверять с помощью математических операций, таких как деление и нахождение остатка от деления. Это позволяет определить, является ли число кратным, и отличить его от чисел, которые не являются кратными данному числу.
В математике кратность используется для описания отношения между числами и может иметь важное значение при решении задач в различных областях, таких как алгебра, арифметика, геометрия и др.
Правила определения кратного числа

1. Правило остатка: Число A кратно числу B, если при делении A на B получается остаток 0. Формально записывается как: A mod B = 0, где mod — операция взятия остатка.
2. Правило делимости: Число A кратно числу B, если A делится на B без остатка. Формально записывается как: A / B = C, где C — целое число.
3. Правило произведения: Число A кратно числу B, если A является произведением числа B на некоторое другое целое число. Формально записывается как: A = B * C, где C — целое число.
Например: чтобы определить, кратно ли число 10 числу 5, можно использовать правило остатка: 10 mod 5 = 0, значит число 10 кратно числу 5.
Важно отметить, что кратность числа всегда относительна другого числа, поэтому при определении кратности необходимо указывать, кратно ли число A числу B.
Кратность числа: примеры из жизни

1. Расписание общественного транспорта
Часто расписание общественного транспорта составляется с учетом кратности определенных интервалов времени. Например, автобус может отправляться каждые 15 минут или каждый час. В этом случае, кратность числа определяет, через какой промежуток времени будет осуществляться следующий рейс.
2. Повторение событий
Кратность числа также может использоваться для определения периодичности повторения событий. Например, если мероприятие проводится каждый год, то его кратность будет равна 1. Если оно проводится каждый два года, то кратность будет равна 2 и так далее.
3. Цикличность явлений природы
Некоторые явления природы происходят с определенной периодичностью. Например, полнолуние повторяется примерно каждые 29 дней. Такая периодичность является примером кратности числа.
4. Кратные задачи
В решении математических задач часто приходится сталкиваться с понятием кратности числа. Например, если требуется найти наименьшее общее кратное двух чисел, то это означает, что нужно найти наименьшее число, которое делится без остатка и на первое число, и на второе число.
Таким образом, понятие кратности числа применимо не только в математике, но и в различных сферах нашей жизни. Оно помогает нам определить периодичность событий, контролировать время, а также решать практические задачи.
Интересные факты о кратных числах
В математике кратные числа играют важную роль и имеют свои особенности. Вот несколько интересных фактов о кратных числах:
- Кратные числа всегда делятся на свои делители без остатка. Например, число 12 является кратным числом для чисел 1, 2, 3, 4, 6 и 12.
- Кратные числа могут быть положительными и отрицательными. Например, -6 и 6 являются кратными числами для числа 3.
- Если число является кратным для двух различных чисел, то оно также будет кратным для их наименьшего общего кратного. Например, число 12 кратно и числу 3, и числу 4, а их наименьшее общее кратное равно 12.
- Кратные числа могут быть использованы для решения различных задач. Например, они могут помочь найти общий период повторения в десятичной дроби или найти наименьшее общее кратное для двух чисел.
- Кратные числа также имеют свои применения в научных и технических расчетах. Они помогают упростить и систематизировать математические модели и формулы.
Изучение кратных чисел позволяет лучше понять многие аспекты математики и применять их в практических задачах. Это важный аспект образования и развития математического мышления.
Кратное числа: практическое применение
Одним из примеров практического применения кратных чисел является арифметика и расчеты в экономике. В экономических расчетах часто используются кратные числа для упрощения и удобства. Например, при расчете цен на товары или услуги, их часто округляют до ближайшего кратного числа для удобства подсчетов.
Еще одним примером практического применения кратных чисел является время. Время часто измеряется и выражается в кратных единицах, таких как часы, минуты и секунды. Например, мы говорим о том, что в сутках 24 часа, а в часе 60 минут. Это позволяет нам удобно измерять и организовывать время в повседневной жизни.
Кроме того, кратные числа имеют практическое применение в науке и технологиях. Например, в физике при измерении величин используются единицы измерения, которые являются кратными друг другу. Это позволяет удобно проводить расчеты и сравнивать различные физические величины.
Таким образом, понятие кратных чисел имеет широкое практическое применение в различных областях нашей жизни. Оно помогает упростить расчеты, измерения и организацию времени, что делает нашу жизнь более удобной и эффективной.
Кратные числа и разложение на множители
Кратные числа имеют широкое применение в различных областях математики и науки. Они могут использоваться для определения общих свойств чисел, решения уравнений, вычисления вероятностей и многое другое.
Разложение на множители — это процесс представления числа в виде произведения простых множителей. Простые числа — это числа, которые имеют только два делителя — 1 и само число. Разложение на множители позволяет нам лучше понять структуру числа и использовать его свойства для решения различных задач.
Например, число 30 может быть разложено на множители следующим образом: 30 = 2 * 3 * 5. Это означает, что 30 можно представить в виде произведения трех простых чисел — 2, 3 и 5.
Разложение на множители является важным инструментом для работы с кратными числами. Оно позволяет нам анализировать свойства чисел и осуществлять различные операции, такие как нахождение наибольшего общего делителя, нахождение кратного числа и многое другое.
Вопрос-ответ:
Что такое кратное числа?
Кратным числом называется такое число, которое делится на другое число без остатка. Например, число 6 является кратным числу 3, потому что 6 делится на 3 без остатка.
Как определить, является ли число кратным другому числу?
Чтобы определить, является ли число кратным другому числу, нужно разделить первое число на второе и проверить, есть ли остаток. Если остатка нет, то число является кратным.
Как найти все кратные числа для заданного числа?
Чтобы найти все кратные числа для заданного числа, нужно последовательно умножать это число на все натуральные числа. Например, для числа 3 все его кратные числа будут: 3, 6, 9, 12, и т.д.
Может ли число быть кратным самому себе?
Да, число может быть кратным самому себе. В математике такие числа называются кратными числами. Например, число 5 является кратным самому себе, потому что 5 делится на 5 без остатка.
Какие свойства имеют кратные числа?
Кратные числа имеют несколько свойств. Во-первых, они всегда делятся на свои делители без остатка. Во-вторых, кратные числа образуют арифметическую прогрессию. Например, все кратные числа для числа 3 образуют прогрессию 3, 6, 9, 12 и т.д.
Что такое кратное в математике?
Кратное в математике — это число, которое делится на другое число без остатка. Например, 10 — кратное числа 5, так как 10 делится на 5 без остатка.
Как определить, является ли число кратным другому числу?
Для того чтобы определить, является ли число кратным другому числу, достаточно проверить, делится ли это число на другое число без остатка. Если деление происходит без остатка, то число является кратным, в противном случае — нет.


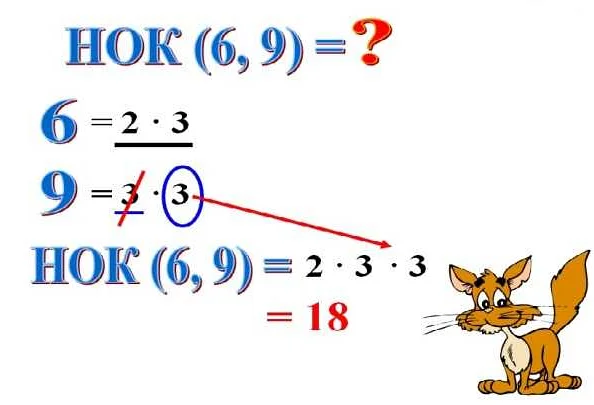
Статья очень понятно объясняет понятие кратного в математике. Я всегда думал, что знаю эту тему, но оказалось, что у меня были пробелы в знаниях. Статья дает простые примеры и пошагово объясняет, как определить, является ли число кратным другому. Очень полезно, что в статье описаны основные свойства кратности, такие как свойство кратного нулю и свойство кратного числа самому себе. Теперь я точно знаю, что такое кратное и как его определить. Большое спасибо автору за такую информативную статью!
Кратное — это понятие из математики, которое иногда может вызывать затруднения в понимании. По определению, число A называется кратным числа B, если оно делится на B без остатка. Например, если число 10 делится на 5 без остатка, то 10 является кратным числу 5. Определить, является ли одно число кратным другому, можно просто поделив первое на второе и проверив, равна ли остатку нулю. Если да, то число кратное, если нет — то нет. Правильное понимание этого концепта важно в различных областях жизни, например при решении задач по финансам, времени или в науке. Поэтому, зная, что такое кратное, мы можем применять этот термин в повседневной жизни и в образовательных целях.
Кратное число — это число, которое делится на другое число без остатка. В математике, это понятие очень важно и часто используется для решения различных задач. Например, если мы хотим узнать, является ли число кратным 5, мы должны проверить, делится ли оно на 5 без остатка. Для определения кратности числа, мы можем использовать различные методы. Самый простой способ — это проверить, делится ли число на данное число без остатка. Например, если мы хотим проверить, является ли число 10 кратным 5, мы можем разделить 10 на 5. Если результат деления равен целому числу, значит число 10 кратно 5. Однако, кратность числа может быть определена не только путем деления. Некоторые числа имеют определенные свойства, которые могут помочь нам определить кратность. Например, для определения кратности числа 2, нам достаточно проверить последнюю цифру числа. Если эта цифра четная, то число кратно 2. Кратное число — это очень полезное понятие в математике, и его понимание поможет решить множество задач. Поэтому, зная основные методы определения кратности, мы можем эффективно применять их в практике.