Кратное это что в математике

Кратное в математике — это число, которое делится на другое число без остатка. Узнайте, что такое кратное, как его вычислять и применять в различных математических операциях.

Математика – это наука о числах и их взаимоотношениях. В ее основе лежат различные понятия, такие как кратность числа. Кратность – это свойство числа быть равным произведению другого числа на целое число. Если одно число делится на другое без остатка, то первое называется кратным второго. Кратное число можно представить в виде произведения множителей, включая само число и его единицу.

Например, число 8 кратно числу 4, так как 8 можно представить в виде произведения 4 и 2: 8 = 4 * 2. Также число 8 кратно числу 1, так как 8 * 1 = 8. Однако число 8 не является кратным числу 3, потому что не существует целого числа, при умножении на которое получится 8.

Кратность имеет много практических применений. В математике она используется для нахождения общего кратного двух или более чисел, для решения линейных уравнений и систем уравнений, а также для изучения периодичности в различных областях науки и техники.

Важно отметить, что кратность может быть полезной не только при работе с целыми числами, но и с дробными и отрицательными числами. Например, дробь 1/2 является кратной дробью 1/4, так как 1/2 = (1/4) * 2. Также число -6 является кратным числу -3, так как -6 = (-3) * 2.

В заключение, кратность – важное и широко применяемое понятие в математике. Оно позволяет определить, делится ли одно число на другое без остатка, и находить общие кратные. Понимание этого понятия поможет в решении различных задач и применении математики в повседневной жизни.

Кратное в математике: определение и примеры

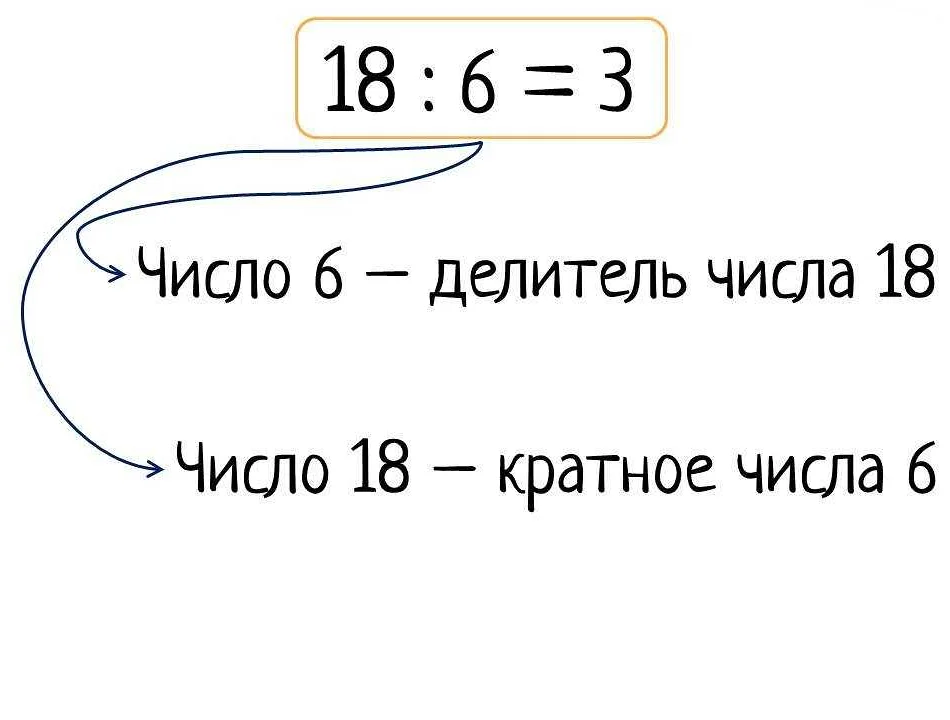
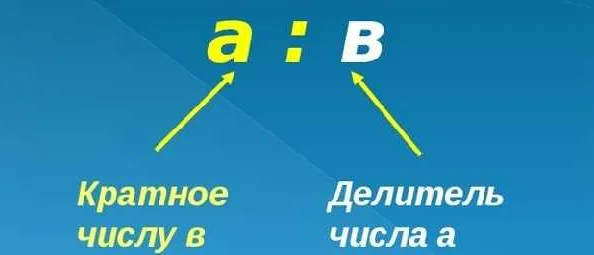
Другими словами, если число a делится на число b без остатка, то a является кратным числом для b. В этом случае мы также говорим, что b является делителем для a.

Например, число 12 является кратным числу 3, потому что 12 делится на 3 без остатка. Также число 24 является кратным числу 6, потому что 24 делится на 6 без остатка.

Кратные числа могут быть положительными и отрицательными. Например, число -9 является кратным числу 3, так как -9 делится на 3 без остатка.

Кратные числа широко используются в математике, особенно в арифметических операциях и делении.

Что такое кратное в математике?

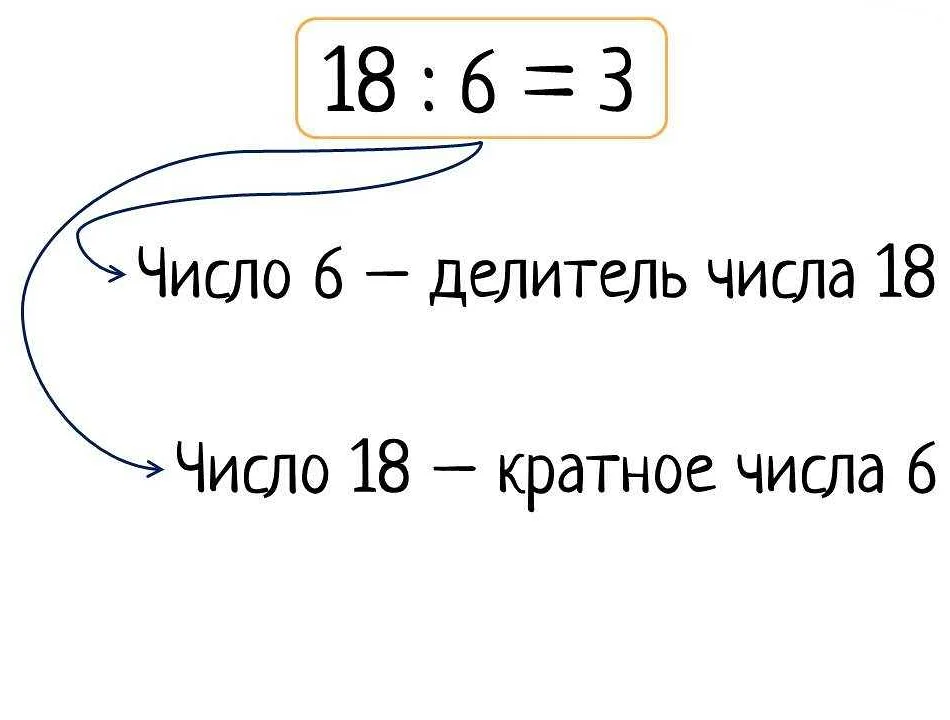
Кратным называется число, которое делится на другое число без остатка. Если число a делится на число b без остатка, то говорят, что a кратно b.

Например, число 12 кратно 3, так как 12 делится на 3 без остатка. Также число 15 кратно 5, так как 15 делится на 5 без остатка.

Кратность используется в различных областях математики и науки. Например, в арифметике кратность может помочь определить делимость чисел и решить различные задачи. В теории чисел кратность используется для изучения свойств чисел и поиска закономерностей. Также кратность может быть полезна в алгебре, геометрии и других разделах математики.

Для проверки кратности числа a числу b можно использовать деление с остатком. Если при делении числа a на число b остаток равен нулю, то число a кратно числу b.

Например, для проверки кратности числа 24 числу 8 можно выполнить деление: 24 ÷ 8 = 3. Остаток равен нулю, поэтому число 24 кратно числу 8.

Кратность является важным понятием в математике и используется для решения различных задач и построения математических моделей. Понимание кратности поможет вам лучше понять и применять математические концепции в реальном мире.

Кратное числа: основные понятия

Кратным числом называется число, которое делится на другое число без остатка. Если число a делится на число b, то число a называется кратным числом числа b, и число b называется делителем числа a.

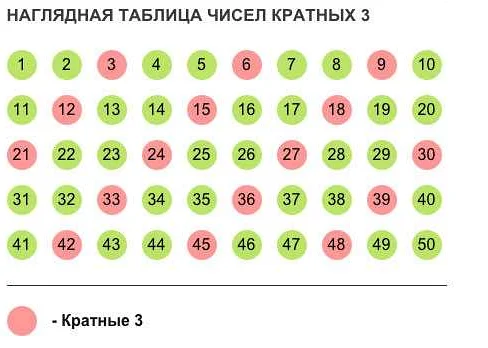
Другими словами, кратное числа получается путем умножения данного числа на натуральное число. Например, числа 6, 12 и 18 являются кратными числами числа 3, так как они делятся на 3 без остатка.

Кратные числа могут быть положительными и отрицательными. Например, -6, -12 и -18 также являются кратными числами числа 3.

Чтобы определить, является ли число кратным другому числу, необходимо разделить число на данное число и проверить, получается ли деление без остатка. Если деление без остатка, то число является кратным, иначе – не является кратным.

Кратные числа широко используются в математике, физике и других науках для решения различных задач. Они помогают с определением симметрии в графиках функций, нахождением общего кратного для двух чисел, а также в других областях.

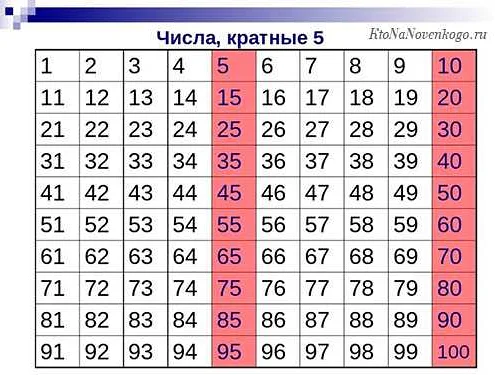
Чтобы лучше понять понятие кратных чисел, рассмотрим примеры. Числа 10, 20, 30, 40 и т.д. являются кратными числа числа 10, так как они делятся на 10 без остатка. А числа 5, 15, 25, 35 и т.д. являются кратными числа числа 5, так как они делятся на 5 без остатка.

Таким образом, кратное число представляет собой множество чисел, которые делятся на данное число без остатка.

Кратное числа: особенности

Особенностью кратных чисел является то, что они образуют последовательность. Например, все числа, кратные 2, образуют последовательность 2, 4, 6, 8, 10 и т.д. Каждое следующее число в этой последовательности получается путем прибавления к предыдущему числу кратного числа 2.

Кратные числа широко используются в математике, науках и повседневной жизни. Они помогают в решении различных задач, например, в арифметических операциях, в изучении пропорций и отношений, в расчетах процентов и многом другом.

Знание особенностей кратных чисел поможет вам лучше понять и использовать их в различных ситуациях, где требуется работа с числами.

Примеры кратных чисел

Вот несколько примеров кратных чисел:

1. Число 6 кратно числам 1, 2 и 3, так как оно делится на них без остатка.
2. Число 10 кратно числам 1, 2 и 5, так как оно делится на них без остатка.
3. Число 15 кратно числам 1, 3 и 5, так как оно делится на них без остатка.
4. Число 20 кратно числам 1, 2, 4, 5 и 10, так как оно делится на них без остатка.

Можно заметить, что все числа кратны самому себе и единице, так как они без остатка делятся на них.

Кратное числа и деление

Для определения, является ли число кратным другому числу, можно использовать деление с остатком. Если остаток от деления равен нулю, то первое число кратно второму. Например, число 12 кратно числу 3, так как при делении 12 на 3 остаток равен нулю.

Кратные числа широко используются в математике и на практике. Например, в календаре каждый год делится на 4 без остатка является високосным. Это означает, что количество дней в году кратно 4.

ЧислоДелительРезультат деленияОстатокКратное?

10	2	5	0	Да
15	4	3	3	Нет
24	6	4	0	Да

В таблице приведены примеры чисел и их делителей. Результат деления и остаток показывают, является ли число кратным. Если остаток равен нулю, то число кратно, если остаток не равен нулю, то число не является кратным.

Кратность и остаток от деления

Когда одно число делится на другое, мы можем определить, насколько это число кратно другому числу и какой остаток остается после деления.

Кратность — это количество раз, которое одно число содержится в другом числе без остатка. Например, число 10 кратно числу 5, потому что 5 содержится в 10 два раза без остатка.

Пример:

10 ÷ 5 = 2

Остаток от деления — это число, которое остается после того, как одно число делится на другое. Остаток может быть равным нулю или быть положительным числом, меньшим делителя. Например, при делении числа 10 на 3, остаток будет равен 1.

Пример:

10 ÷ 3 = 3 (остаток 1)

Используя понятия кратности и остатка от деления, мы можем решать различные задачи в математике, такие как нахождение наименьшего общего кратного двух чисел или проверка делимости чисел на конкретное число.

Видео по теме:

Вопрос-ответ:

Что такое кратное в математике?

Кратное число — это число, которое делится на другое число без остатка. Если число a делится на число b без остатка, то a называется кратным числом для b.

Как определить, что число является кратным другому числу?

Чтобы определить, что число a является кратным числу b, нужно проверить, делится ли a на b без остатка. Если делится, то a является кратным числом для b.

Какие числа являются кратными 5?

Числа, которые заканчиваются на 0 или 5, являются кратными 5. Например, числа 10, 15, 20 и так далее, все они делятся на 5 без остатка.

Что будет, если число не является кратным другому числу?

Если число a не делится на число b без остатка, то a не является кратным числом для b.

Какие числа являются кратными 3 и 4 одновременно?

Чтобы число являлось кратным 3 и 4 одновременно, оно должно быть кратно и 3, и 4 одновременно. Например, числа 12, 24, 36 и так далее, все они делятся и на 3, и на 4 без остатка.

Кратные числа и кратность

Кратность — это количество раз, которое одно число содержит другое число в себе.

Например, число 6 является кратным числом числа 3, потому что можно получить, умножив 3 на 2. В данном случае, число 2 — это количество раз, которое число 3 содержит в себе число 6.

Также, число 10 является кратным числом числа 5, потому что можно получить, умножив 5 на 2. В данном случае, число 2 — это количество раз, которое число 5 содержит в себе число 10.

В математике, кратность может быть определена с использованием деления с остатком. Если остаток от деления одного числа на другое равен нулю, значит, это число кратно другому числу.

Значение кратных чисел в математике

Кратные числа играют важную роль в арифметике, алгебре и других разделах математики. Они позволяют решать задачи связанные с разделением и сравнением количества объектов.

Например, если число A кратно числу B, то можно сказать, что число A содержит в себе «несколько» или «множество» копий числа B. Если число A не кратно числу B, то это означает, что число A содержит в себе меньше или больше «несколько» или «множество» копий числа B.

Кратные числа также используются при работе с дробями и процентами. Например, если число A кратно числу B, то можно сказать, что дробь A/B равна целому числу. Если число A не кратно числу B, то дробь A/B будет представлять собой десятичную дробь или рациональное число.

Понимание кратных чисел позволяет решать многочисленные задачи в математике и на практике. Например, кратные числа используются для расчета времени, деления ресурсов и многое другое.