На рисунке 87 представлены графики колебаний трех математических маятников укажите чем отличаются

На рисунке 87 показаны графики трех математических маятников, отличающихся по длине или массе. Изучая эти графики, можно увидеть, как меняются колебания маятников в зависимости от их параметров.

На рисунке 87 представлены графики колебаний трех математических маятников. Каждый маятник имеет свои уникальные характеристики, которые отражаются в его графике колебаний.

Первый маятник обладает большой амплитудой и малой частотой колебаний. Его график представляет собой широкую кривую, которая медленно осциллирует вокруг равновесной точки. Длительность каждого периода колебаний достаточно велика, что создает впечатление плавности движения.

Второй маятник отличается от первого меньшей амплитудой и большей частотой колебаний. Его график представляет собой более узкую кривую, которая быстро осциллирует вокруг равновесной точки. Колебания второго маятника более резкие и частота их изменений значительно выше.

Третий маятник имеет средние значения амплитуды и частоты колебаний. Его график представляет собой среднюю кривую, которая осциллирует вокруг равновесной точки с умеренной скоростью. Колебания третьего маятника не такие резкие, как у второго, но и не такие плавные, как у первого.

Таким образом, графики колебаний трех математических маятников на рисунке 87 демонстрируют различия в их амплитуде, частоте и резкости колебаний. Каждый маятник имеет свою уникальную динамику, которая отражается в его графике и создает различие в восприятии движения.

Различия графиков колебаний

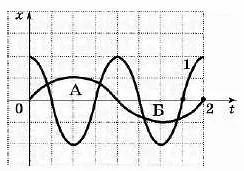
На рисунке 87 представлены графики колебаний трех математических маятников. Эти графики отражают зависимость координаты маятника от времени в процессе его колебаний.

Первый график соответствует гармоническому маятнику, который описывает осцилляции с постоянной амплитудой и периодом. Колебания этого маятника характеризуются равномерной и симметричной формой графика, где координата маятника меняется синусоидально в зависимости от времени.

Второй график отображает апериодический маятник, который не обладает постоянной амплитудой и периодом. Здесь наблюдаются затухающие колебания, где амплитуда постепенно уменьшается с течением времени. Форма графика не является симметричной и может быть различной в зависимости от начальных условий.

Третий график представляет собой периодически затухающие колебания, которые характеризуются убывающей амплитудой и постоянным периодом. График имеет схожую форму с гармоническим маятником, но с каждым колебанием амплитуда уменьшается и сходится к нулю.

Таким образом, графики колебаний трех математических маятников на рисунке 87 отличаются по форме, амплитуде и периоду. Эти различия связаны с особенностями каждого маятника и его начальными условиями.

МаятникФорма графикаАмплитудаПериод

Гармонический	Симметричная синусоида	Постоянная	Фиксированный
Апериодический	Несимметричная форма	Убывающая	Неопределенный
Периодически затухающий	Схожая с гармоническим	Убывающая	Фиксированный

Три математических маятника

На рисунке 87 представлены графики колебаний трех математических маятников. Каждый из маятников имеет свои особенности, которые приводят к различным формам колебаний.

Первый маятник, обозначенный линией А, имеет среднее время периода колебаний и симметричную форму графика. Его колебания можно описать как равномерные и регулярные.

Второй маятник, обозначенный линией В, имеет более быстрое время периода колебаний по сравнению с первым маятником. График его колебаний обладает более остро выраженными экстремумами и меньшей амплитудой.

Третий маятник, обозначенный линией С, имеет самое быстрое время периода колебаний среди трех маятников. График его колебаний является несимметричным и имеет большую амплитуду по сравнению с первыми двумя маятниками.

Таким образом, каждый из трех математических маятников имеет свои характеристики, которые определяют его график колебаний.

На рисунке 87

Представлены графики колебаний трех математических маятников. Каждый маятник имеет свою массу и длину, что влияет на его период колебаний.

Первый маятник имеет массу 1 кг и длину 1 метр. Его график колебаний представляет собой синусоиду с постоянной амплитудой и периодом, зависящим от его длины.

Второй маятник имеет массу 2 кг и длину 0,5 метра. График его колебаний отличается от графика первого маятника, так как его период колебаний также зависит от его массы.

Третий маятник имеет массу 1 кг и длину 0,5 метра. Его график колебаний схож с графиком первого маятника, но имеет меньшую амплитуду и более короткий период колебаний из-за его меньшей длины.

Форма графиков

На рисунке 87 представлены графики колебаний трех математических маятников. Каждый график отображает зависимость амплитуды колебаний от времени. Отличительные особенности формы графиков позволяют сравнить характер колебаний в трех различных маятниках.

График первого маятника характеризуется равномерным, периодическим колебанием с постоянной амплитудой. Верхняя точка графика соответствует положению маятника в покое, а нижняя точка — крайнему отклонению маятника от положения равновесия.

График второго маятника имеет аналогичную форму, но с большей амплитудой. Это говорит о том, что второй маятник имеет большую энергию и совершает более широкие колебания.

График третьего маятника отличается от предыдущих двух. Он имеет более сложную форму, с периодическими изменениями амплитуды. Это свидетельствует о наличии диссипации энергии и затухании колебаний. По мере времени амплитуда колебаний третьего маятника уменьшается.

График маятника 1	График маятника 2	График маятника 3

Периоды колебаний

Первый маятник на рисунке имеет наибольшую длину подвеса и массу груза. Это делает его период колебаний наибольшим по сравнению с остальными маятниками. Второй маятник имеет средние значения длины подвеса и массы груза, что делает его период колебаний средним. Третий маятник имеет самую короткую длину подвеса и массу груза, и его период колебаний является наименьшим.

МаятникДлина подвесаМасса грузаПериод колебаний

Первый	Длинная	Тяжелая	Большой
Второй	Средняя	Средняя	Средний
Третий	Короткая	Легкая	Маленький

Из таблицы видно, что период колебаний каждого маятника зависит от его длины подвеса и массы груза. Более длинный подвес и более тяжелый груз приводят к увеличению периода колебаний, а более короткий подвес и более легкий груз — к его уменьшению.

Амплитуды колебаний

На рисунке 87 представлены три графика колебаний трех математических маятников. Каждый из маятников имеет свою амплитуду колебаний, которая отличается от амплитуды других маятников. Амплитуда колебаний может быть различна как по величине, так и по направлению.

Значение амплитуды колебаний влияет на характер движения математического маятника. Чем больше амплитуда, тем больше энергии тратится на колебания и тем дольше продолжается их движение. Малые амплитуды обычно сопровождаются быстрыми и короткими колебаниями, а большие амплитуды — медленными и продолжительными колебаниями.

Таким образом, амплитуды колебаний являются важными характеристиками математических маятников, определяющими их движение и поведение в пространстве.

Фазы колебаний

Фаза колебаний математического маятника определяется положением маятника в определенный момент времени относительно его равновесного положения. На рисунке 87 представлены графики колебаний трех математических маятников.

Первый маятник имеет одну фазу колебаний, которая характеризуется тем, что маятник проходит через свое равновесное положение дважды за один период колебаний. Второй маятник имеет две фазы колебаний, потому что он проходит через свое равновесное положение четыре раза за один период колебаний. Третий маятник имеет три фазы колебаний, так как он проходит через свое равновесное положение шесть раз за один период колебаний.

Фазы колебаний позволяют определить взаимные положения маятников в определенный момент времени. Например, если первый и второй маятники находятся в своих равновесных положениях одновременно, то они находятся в одной фазе колебаний. Если же первый маятник находится в своем равновесном положении, а второй маятник находится в положении максимального отклонения, то они находятся в противофазе колебаний.

Знание фаз колебаний математических маятников позволяет предсказывать их будущие положения и взаимодействия друг с другом. Фазы колебаний также играют важную роль в различных областях науки и техники, где используются колебания и волны.

Зависимость от начальных условий

Математические маятники на рисунке 87 демонстрируют различные графики колебаний, которые зависят от начальных условий. Начальные условия определяются амплитудой и фазой колебаний, а также начальной скоростью маятника.

В первом маятнике начальная амплитуда колебаний равна 1, а фаза равна 0. Это означает, что маятник начинает свое движение из положения равновесия и колеблется вокруг этого положения с постоянной амплитудой.

Во втором маятнике начальная амплитуда колебаний равна 2, а фаза равна π/2. Это означает, что маятник начинает свое движение из крайнего положения и колеблется между крайними положениями, достигая максимальной амплитуды в момент времени, равном π/2.

В третьем маятнике начальная амплитуда колебаний равна 1, а начальная скорость равна 1. Это означает, что маятник начинает свое движение с некоторой начальной скоростью и колеблется вокруг положения равновесия с уменьшающейся амплитудой.

Таким образом, различия в графиках колебаний трех математических маятников на рисунке 87 связаны с различными начальными условиями, которые определяют их движение.

Вопрос-ответ:

Какие различия можно наблюдать на графиках колебаний трех математических маятников на рисунке 87?

На графиках колебаний трех математических маятников на рисунке 87 можно наблюдать различия в амплитуде колебаний, периоде колебаний и фазовом сдвиге.

Как можно описать различия в амплитуде колебаний трех математических маятников на рисунке 87?

На графиках колебаний трех математических маятников на рисунке 87 можно видеть, что амплитуда колебаний первого маятника максимальна, второго меньше, а третьего — наименьшая.

Какие различия можно выделить в периодах колебаний трех математических маятников на рисунке 87?

На графиках колебаний трех математических маятников на рисунке 87 можно заметить, что период колебаний первого маятника наибольший, второго меньше, а третьего — наименьший.

Каким образом можно описать различия в фазовом сдвиге колебаний трех математических маятников на рисунке 87?

На графиках колебаний трех математических маятников на рисунке 87 можно заметить, что фазовый сдвиг колебаний между первым и вторым маятниками составляет примерно 90 градусов, а между вторым и третьим маятниками — примерно 180 градусов.

Как можно описать общие различия в колебаниях трех математических маятников на рисунке 87?

Общие различия в колебаниях трех математических маятников на рисунке 87 заключаются в уменьшении амплитуды и периода колебаний с увеличением номера маятника, а также в увеличении фазового сдвига между маятниками.

Какие различия можно наблюдать на графиках колебаний трех математических маятников на рисунке 87?

На графиках колебаний трех математических маятников на рисунке 87 можно заметить различия в амплитуде, периоде и фазе колебаний. У первого маятника амплитуда максимальна, период колебаний равен 1 секунде, а фаза начинается с максимального значения. У второго маятника амплитуда меньше, период колебаний равен 2 секундам, а фаза начинается с минимального значения. У третьего маятника амплитуда еще меньше, период колебаний равен 3 секундам, а фаза начинается с нулевого значения.

Какие особенности наблюдаются на графике колебания первого математического маятника на рисунке 87?

На графике колебания первого математического маятника на рисунке 87 можно заметить, что амплитуда колебаний максимальна. Это означает, что маятник отклоняется наибольшим образом от положения равновесия. Период колебаний составляет 1 секунду, что означает, что маятник совершает один полный цикл колебаний за 1 секунду. Фаза начинается с максимального значения, что означает, что маятник находится в крайней точке своего движения при начале отсчета времени.

Видео по теме: