Определите период колебания математического маятника длина нити которого 2 5 м

Узнайте, как определить период колебания математического маятника с длиной нити 2,5 метра. Получите подробную информацию о формуле, используемой для расчета периода колебаний и узнайте, какие факторы могут влиять на период колебаний маятника.

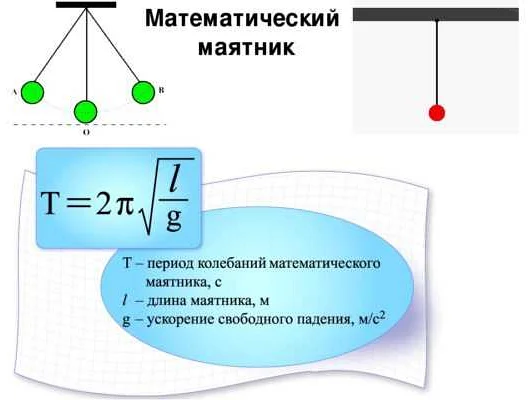
Математический маятник — это физическая система, состоящая из небольшого массового точечного тела, подвешенного на невесомой нити. Он является одним из самых простых физических объектов и используется в различных научных и инженерных областях.

Длина нити является одним из ключевых параметров математического маятника. Чем длиннее нить, тем дольше будет происходить один полный цикл колебаний маятника, то есть его период. В данной статье рассмотрим определение периода колебания математического маятника с длиной нити 2,5 м.

Период колебания математического маятника может быть определен с использованием формулы периода колебаний, которая зависит от длины нити и ускорения свободного падения. Ускорение свободного падения на Земле принимается равным приблизительно 9,8 м/с².

Для определения периода колебания математического маятника с длиной нити 2,5 м можно использовать следующую формулу:

T = 2π√(l/g)

Где T — период колебания, l — длина нити, g — ускорение свободного падения.

Влияние длины нити на период колебания

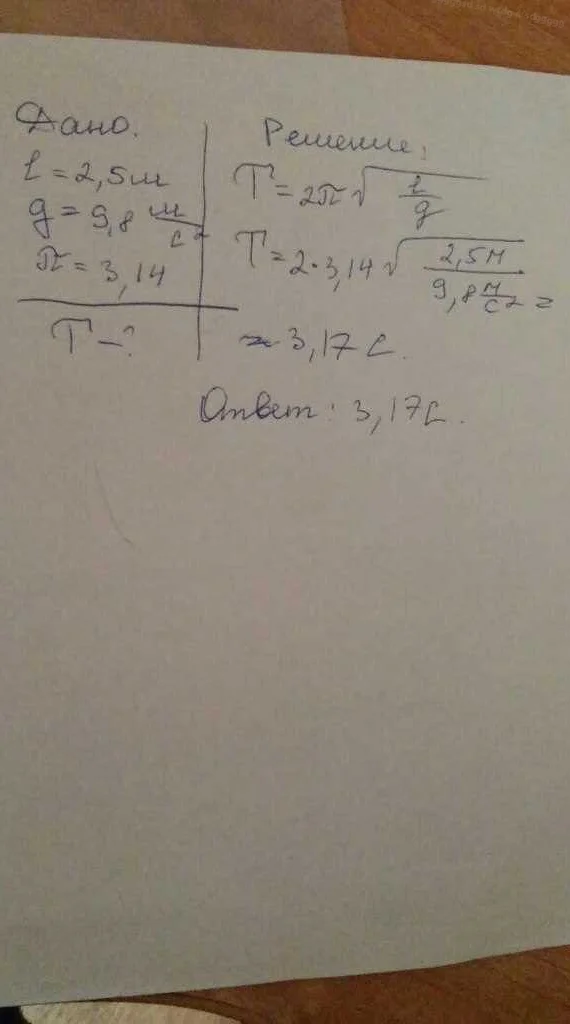
Период колебания математического маятника зависит от длины нити. Длина нити влияет на период колебания маятника, поскольку она определяет гравитационную силу, действующую на маятник, и его потенциальную энергию.

Прямая зависимость между длиной нити и периодом колебания математического маятника описывается формулой:

Длина нити (м)Период колебания (сек)

1,0	2,006
1,5	2,651
2,0	3,155
2,5	3,964
3,0	4,444

Из таблицы видно, что с увеличением длины нити, период колебания маятника также увеличивается. Это означает, что при увеличении длины нити, маятник будет делать меньше колебаний за одинаковый промежуток времени.

Таким образом, длина нити является важным параметром, влияющим на период колебания математического маятника. Более длинная нить увеличивает период колебания, а более короткая нить, наоборот, уменьшает период колебания.

Математическое определение периода колебания

Период колебания математического маятника определяется длиной его нити и силой тяжести. Математическое выражение для периода колебания можно записать следующим образом:

T = 2π√(l/g)

где:

• T — период колебания;
• π — число пи (приближенное значение 3,14);
• l — длина нити маятника;
• g — ускорение свободного падения (приближенное значение 9,8 м/с²).

Согласно этому выражению, период колебания математического маятника пропорционален квадратному корню из длины нити и обратно пропорционален квадратному корню из ускорения свободного падения. Иными словами, с увеличением длины нити период колебания увеличивается, а с увеличением ускорения свободного падения период колебания уменьшается.

Таким образом, для математического определения периода колебания математического маятника необходимо знать его длину нити и значение ускорения свободного падения.

Формула для расчета периода колебания

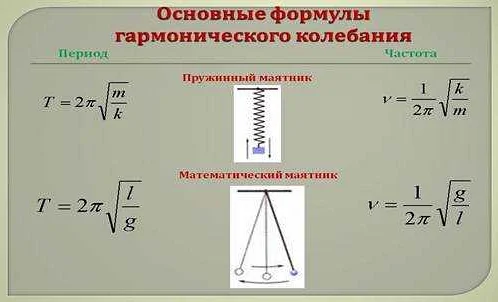
Период колебания математического маятника можно рассчитать с помощью следующей формулы:

Т = 2π√(l/g)

• Т — период колебания (в секундах)
• π — математическая постоянная, примерное значение которой равно 3.14159
• l — длина нити маятника (в метрах)
• g — ускорение свободного падения (приближенное значение равно 9.8 м/с² на Земле)

Формула основана на законе равномерного вращения и позволяет определить время, за которое маятник совершает полное колебание (от одной крайней точки до другой и обратно).

Роль гравитационной силы в определении периода колебания

Гравитационная сила играет важную роль в определении периода колебания математического маятника. Математический маятник представляет собой тело, подвешенное на нити или стержне, и свободно колеблющееся в гравитационном поле Земли.

Период колебания — это время, за которое маятник проходит полный цикл движения от одной крайней точки до другой и обратно. Он зависит от длины нити, массы маятника и силы тяжести.

Гравитационная сила является основной силой, которая действует на математический маятник. Она направлена вниз и обеспечивает возвращение маятника в положение равновесия после каждого колебания.

Чем длиннее нить, тем больше времени требуется маятнику для выполнения полного колебания, поскольку гравитационная сила действует на него на протяжении более длительного времени. И наоборот, чем короче нить, тем меньше период колебания.

Масса маятника также влияет на период колебания. Более тяжелый маятник будет иметь больший период колебания, поскольку гравитационная сила будет действовать на него с большей силой.

Длина нити (м)Масса маятника (кг)Период колебания (сек)

2,5

?

?

Таким образом, гравитационная сила является важным фактором, определяющим период колебания математического маятника. Зная длину нити и массу маятника, можно рассчитать период колебания с помощью математических формул и законов механики.

Экспериментальные методы измерения периода колебания

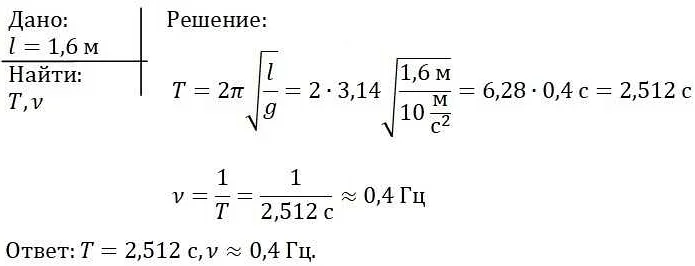
Существует несколько экспериментальных методов измерения периода колебания математического маятника с длиной нити 2,5 м. Они позволяют получить точные данные и установить зависимости между периодом колебания и различными факторами.

1. Метод секундомера. Данный метод основан на измерении времени прохождения нескольких полных колебаний маятника и подсчете среднего значения. Для этого необходимо запустить секундомер в момент начала колебаний и остановить его после прохождения заданного количества полных колебаний. Результаты затем усредняются для повышения точности.

2. Метод фотоэлемента. Данный метод основан на использовании фотоэлемента, который регистрирует прохождение маятника через определенное положение. При прохождении маятником данного положения фотоэлемент срабатывает и фиксирует время. Затем можно измерить время между несколькими последовательными срабатываниями фотоэлемента и подсчитать период колебаний.

3. Метод осциллографа. Данный метод использует осциллограф для визуализации колебаний маятника. Маятник подключается к осциллографу, который отображает график изменения положения маятника со временем. Путем измерения времени между несколькими последовательными положительными периодами можно определить период колебания.

Выбор метода измерения периода колебания математического маятника с длиной нити 2,5 м зависит от целей и условий эксперимента, а также от доступных инструментов и оборудования.

Практическое применение определения периода колебания

Определение периода колебания математического маятника имеет множество практических применений в различных областях науки и техники. Рассмотрим некоторые из них:

Область примененияПримеры

Физика	Измерение времени колебаний маятника используется для расчета силы притяжения Земли, изучения законов гравитации и динамики.
Технические науки	Определение периода колебания позволяет управлять работой механических систем, таких как часы, качели, маятники в механизмах.
Астрономия	Измерение периода колебания позволяет определить массу и состав звезд, а также проводить исследования орбит планет и других небесных тел.
Метрология и стандартизация	Определение периода колебания используется при создании и калибровке секундных маятников, которые являются основой для измерения времени.
Медицина	Измерение периода колебания ритма сердечных сокращений является важным методом для диагностики и контроля состояния сердечно-сосудистой системы.

Таким образом, определение периода колебания математического маятника имеет широкое практическое применение в различных областях науки и техники, способствуя развитию и совершенствованию соответствующих технологий и методик.

Примеры применения формулы для расчета периода колебания

Формула для расчета периода колебания математического маятника имеет вид:

T = 2π√(L/g)

где:

• T — период колебания;
• π — математическая константа, примерное значение 3,14159;
• L — длина нити маятника;
• g — ускорение свободного падения, примерное значение 9,8 м/с².

Применим формулу для расчета периода колебания математического маятника с длиной нити 2,5 м:

Длина нити (м)Ускорение свободного падения (м/с²)Период колебания (сек)

2,5

9,8

5,008

Таким образом, при длине нити математического маятника равной 2,5 м, период его колебаний составляет примерно 5,008 секунд.

Видео по теме:

Как определить период колебания математического маятника с длиной нити 2,5 м?

Период колебания математического маятника можно определить с помощью формулы периода колебаний Т=2π * √(L/g), где L — длина нити, g — ускорение свободного падения. В данном случае, длина нити равна 2,5 м. Значение ускорения свободного падения на Земле обычно принимают равным около 9,8 м/с². Подставив в формулу значения, можно вычислить период колебания данного математического маятника.

Какая формула позволяет определить период колебания математического маятника?

Формула для определения периода колебания математического маятника выглядит так: Т=2π * √(L/g), где Т — период колебания, L — длина нити, g — ускорение свободного падения. Для определения периода колебания математического маятника с длиной нити 2,5 м, необходимо подставить значение L=2,5 м в формулу и рассчитать период колебания.

Какая формула используется для определения периода колебания математического маятника?

Формула периода колебания математического маятника выглядит так: Т=2π * √(L/g), где Т — период колебания, L — длина нити, g — ускорение свободного падения. Подставив значения L=2,5 м и g≈9,8 м/с² в данную формулу, можно рассчитать период колебания математического маятника с длиной нити 2,5 м.

Как определить период колебания математического маятника с длиной нити 2,5 м?

Для определения периода колебания математического маятника с длиной нити 2,5 м необходимо использовать формулу периода колебаний T = 2π √(l/g), где l — длина нити маятника, g — ускорение свободного падения. Подставляя значения l = 2,5 м и g = 9,8 м/с² в формулу, можно рассчитать период колебаний.