Разность чисел что это такое в математике 1

Разность чисел в математике 1 – это операция вычитания, которая позволяет найти разницу между двумя числами. В данной статье рассматривается понятие разности чисел, основные правила вычитания и примеры его применения. Узнайте, как правильно вычитать числа и сделать это быстро и точно.

Разность чисел — одна из основных арифметических операций в математике. Она позволяет найти разницу между двумя числами. Разность можно вычислить, вычитая одно число из другого.

Для вычисления разности чисел используется знак вычитания (-). Если первое число больше второго, то разность будет положительной. Если второе число больше первого, то разность будет отрицательной. Если два числа равны, то разность будет равна нулю.

Пример:

Рассмотрим пример вычисления разности чисел. Пусть у нас есть число 7 и число 3. Чтобы найти разность, нужно вычесть из первого числа второе число: 7 — 3 = 4. Таким образом, разность чисел 7 и 3 равна 4.

Разность чисел может быть полезна в различных ситуациях. Например, она может использоваться для нахождения разницы в значениях каких-либо величин, для выяснения изменений во времени или расчета остатка при вычитании.

В заключение, разность чисел — это важная математическая операция, которая позволяет находить разницу между двумя числами. Вычисление разности может помочь в решении различных задач и анализе данных. Знание и понимание этой операции полезно в повседневной жизни и во многих областях науки и техники.

Что такое разность чисел?

Другими словами, разность чисел показывает насколько одно число меньше или больше другого. Если результат вычитания положительный, то первое число больше второго. Если результат отрицательный, то первое число меньше второго.

Разность чисел можно вычислять как с помощью калькулятора, так и в уме. Важно помнить, что порядок вычитания имеет значение. То есть, разность чисел 7 и 3 будет равна 4, но разность чисел 3 и 7 будет равна -4.

Разность чисел широко используется в различных областях, включая финансы, статистику и науку. Она помогает сравнивать величины и определять разницу между ними.

Видео по теме:

Как вычислить разность чисел?

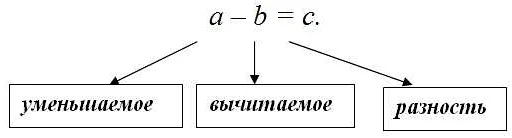
1. Возьмите первое число, которое нужно вычесть, и запишите его.
2. Возьмите второе число, которое нужно вычесть, и запишите его.
3. Поставьте знак минус между двумя числами.
4. Выполните вычитание двух чисел, следуя правилам вычитания.
5. Результатом будет число, которое является разностью двух исходных чисел.

Например, если нужно найти разность чисел 10 и 5, то следуя описанным шагам, получим:

1. 10
2. 5
3. —
4. 10 — 5 = 5

Таким образом, разность чисел 10 и 5 равна 5.

Примеры вычисления разности чисел

Разность чисел можно вычислить, вычитая из одного числа другое. Разность двух чисел обозначается символом «-«. Например, разность чисел 10 и 5 вычисляется следующим образом:

10 — 5 = 5

Разность чисел может быть как положительной, так и отрицательной. Если первое число больше второго, то разность будет положительной. Если первое число меньше второго, то разность будет отрицательной.

Например, разность чисел 8 и 12:

8 — 12 = -4

Также можно вычислить разность чисел с плавающей точкой. Например, разность чисел 3.5 и 1.2:

3.5 — 1.2 = 2.3

Вычисление разности чисел может быть полезным при решении задач по математике, физике, экономике и другим наукам.

Как использовать разность чисел в реальной жизни?

Одним из примеров использования разности чисел является вычисление скидки на товары. Представьте, что вы покупаете товар, который стоит 1000 рублей, но на него действует скидка в размере 300 рублей. Чтобы узнать, сколько вы сэкономите, нужно вычислить разность между стоимостью товара и скидкой: 1000 — 300 = 700 рублей. Таким образом, вы сэкономите 700 рублей.

Еще одним примером использования разности чисел является вычисление временного промежутка. Например, если вы хотите узнать, сколько времени вы потратили на выполнение задачи, вам нужно вычислить разность между начальным и конечным временем. Например, если вы начали задачу в 10:00 и закончили в 12:30, то разность между этими временами будет: 12:30 — 10:00 = 2:30 часов. Таким образом, вы потратили 2 часа и 30 минут на выполнение задачи.

Разность чисел также может использоваться для вычисления расстояния между двумя точками. Например, если у вас есть две точки на координатной плоскости с координатами (2, 4) и (6, 8), то чтобы найти расстояние между ними, нужно вычислить разность между соответствующими координатами: (6 — 2) + (8 — 4) = 4 + 4 = 8. Таким образом, расстояние между этими двуми точками составляет 8 единиц.

Зачем нужно вычислять разность чисел?

Одним из основных применений разности чисел является измерение изменений. Например, если у нас есть два значения какой-либо величины в разные моменты времени, вычисление разности между этими значениями позволяет нам определить, насколько величина изменилась в течение этого времени.

Вычисление разности чисел также используется для сравнения и анализа данных. Например, если у нас есть две группы людей с разными характеристиками, вычисление разности между этими характеристиками может помочь нам понять, какие различия существуют между этими группами и какие факторы влияют на эти различия.

Кроме того, разность чисел используется во многих прикладных областях, таких как физика, экономика, финансы и т. д. В этих областях разность чисел используется для решения различных задач, таких как определение скорости изменения, расчет прибыли или убытка, оценка эффективности и т. д.

Таким образом, вычисление разности чисел является важной и полезной операцией, которая помогает нам измерять различия между величинами, анализировать данные и решать различные задачи в разных областях знания.

Какие свойства имеет разность чисел?

Разность чисел обладает рядом свойств, которые позволяют упростить вычисления и анализировать полученные результаты. Рассмотрим основные свойства разности чисел:

1. Ассоциативность: разность чисел ассоциативна, то есть порядок расстановки скобок не влияет на итоговый результат. Например, разность (а — b) — c равна а — (b + c), где а, b и c — произвольные числа.
2. Коммутативность: разность чисел коммутативна, то есть порядок чисел, вычитаемых друг из друга, не влияет на результат. Например, разность а — b равна — (b — a), где а и b — произвольные числа.
3. Свойство нуля: разность числа на ноль равна самому числу. Например, а — 0 = а, где а — произвольное число.
4. Свойство противоположного числа: разность чисел a — b равна сумме чисел a и -b, где -b является противоположным числом для числа b. Например, a — b = a + (-b), где a и b — произвольные числа.
5. Свойство тождественного нуля: разность числа на само себя равна нулю. Например, а — а = 0, где а — произвольное число.

Знание этих свойств позволяет более эффективно выполнять вычисления и решать задачи, связанные с разностью чисел. Они также помогают проводить анализ полученных результатов и делать выводы о свойствах и особенностях чисел.

Чем отличается разность чисел от других операций?

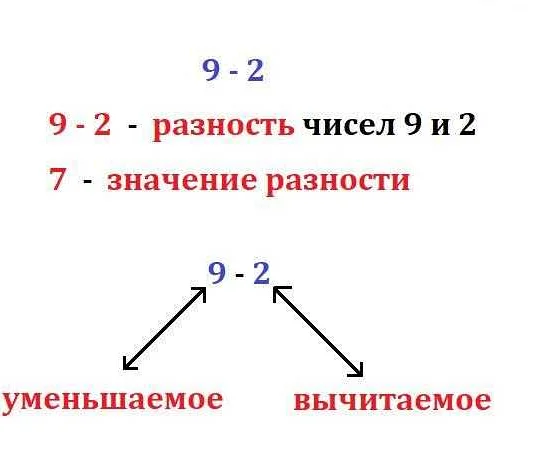
Основное отличие разности чисел от других операций заключается в том, что результат вычисления разности может быть как положительным, так и отрицательным числом. Это зависит от порядка вычитаемых чисел и их величины.

Например, если вычитаемое число больше уменьшаемого, то результат будет отрицательным числом. Напротив, если уменьшаемое число больше вычитаемого, то результат будет положительным числом.

В математике разность чисел обозначается знаком «-» между вычитаемым и уменьшаемым числами. Например, разность чисел 10 и 5 записывается как 10 — 5.

Разность чисел может быть вычислена с помощью таблицы вычитания или алгоритма вычитания в столбик. В результате вычитания получается разность чисел, которая может быть использована для решения различных задач и задач, связанных с изменением количества или величины.

ВычитаемоеУменьшаемоеРазность

10	5	5
7	12	-5
15	20	-5

Таким образом, разность чисел отличается от других операций тем, что она представляет собой вычитание одного числа из другого и может давать как положительные, так и отрицательные результаты.

Вопрос-ответ:

Что такое разность чисел в математике?

Разность чисел в математике — это результат вычитания одного числа из другого.

Как вычислить разность двух чисел?

Для вычисления разности двух чисел нужно первое число уменьшить на второе число. Например, разность чисел 7 и 3 равна 4.

Какие примеры вычислений разности чисел можно привести?

Например, разность чисел 10 и 5 равна 5. Разность чисел 15 и 8 равна 7. Разность чисел 20 и 12 равна 8.

Какая разность чисел будет, если первое число меньше второго?

Если первое число меньше второго, то разность будет отрицательной. Например, разность чисел 3 и 7 будет равна -4.

Есть ли какие-то правила или формулы для вычисления разности чисел?

Для вычисления разности чисел нет специальных правил или формул — нужно просто одно число вычесть из другого. Однако, существуют различные методы и приемы, которые помогают упростить вычисления.

Что такое разность чисел?

Разность чисел — это операция в математике, которая показывает, насколько одно число отличается от другого. Она вычисляется путем вычитания одного числа из другого.