Симметрично это как пример фото в математике

Симметричные фотографии – это пример использования понятия симметрии в математике. Узнайте, как симметрия может быть представлена в изображениях и как она связана с математическими принципами.

Симметрия — одно из фундаментальных понятий математики, которое встречается во многих ее областях. Она отражает особую гармонию и баланс в структуре объектов и явлений. Симметрия может быть обнаружена в абстрактных математических формулах, геометрических фигурах, а также в естественных и искусственных объектах.

Одним из простейших типов симметрии является осевая симметрия. Она характеризуется наличием оси, вокруг которой объект выглядит зеркально симметричным. Например, квадрат, треугольник, круг и другие геометрические фигуры могут обладать осевой симметрией. Этот тип симметрии широко применяется в архитектуре, дизайне и искусстве.

Симметрия также может быть замечена в природе. Многие цветы, как, например, роза или подснежник, имеют симметричную форму, которая привлекает наше внимание и вызывает удивление. Узоры на крыльях бабочек и перьях птиц также являются яркими примерами симметрии в природе.

Фотография — отличный способ запечатлеть и проиллюстрировать симметрию. Фотографы активно используют этот прием в своих работах, чтобы передать гармонию и красоту симметричных объектов. Некоторые известные фотографии, которые демонстрируют симметрию, стали настоящими произведениями искусства.

В данной статье мы рассмотрим различные виды симметрии в математике, приведем интересные примеры симметричных фигур и представим вам красивые фотографии, которые покажут, как симметрия может быть красивой и впечатляющей.

Основные понятия симметрии

Основные понятия симметрии включают:

• Осевую симметрию: ось симметрии является прямой линией, которая делит фигуру на две равные части, симметричные относительно этой оси.
• Плоскую симметрию: плоскость симметрии является плоской поверхностью, которая делит фигуру на две равные части, симметричные относительно этой плоскости.
• Центральную симметрию: центр симметрии является точкой, относительно которой фигура остается симметричной.
• Ротационную симметрию: фигура остается симметричной после поворота на определенный угол вокруг своего центра.

Симметрия широко применяется в различных областях математики, а также в физике, химии и других науках. Она помогает нам понять и описывать законы и свойства объектов и систем, упрощает решение задач и обнаружение закономерностей.

Видео по теме:

Геометрическая симметрия

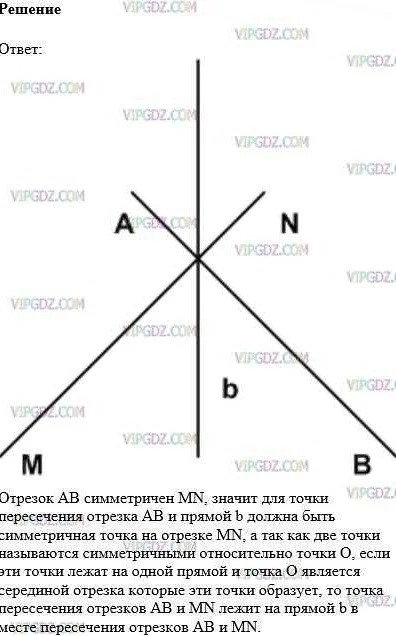
Геометрическая симметрия описывает ситуацию, когда фигура может быть разделена на две равные или зеркальные части относительно некоторой линии или плоскости. В этом случае каждая часть фигуры будет являться зеркальным отражением другой.

Простым примером геометрической симметрии является круг. В круге можно провести бесконечное количество линий симметрии, которые разделяют его на две одинаковые половины. Если мы возьмем одну из половинок и отразим ее относительно линии симметрии, получим исходный круг.

Геометрическая симметрия имеет свои особенности и правила. Например, если фигура имеет центральную симметрию, то каждая точка находится на равном удалении от центра фигуры. Если фигура имеет осевую симметрию, то каждая точка находится на равном удалении от оси симметрии.

Применение геометрической симметрии широко используется в архитектуре, дизайне, изобразительном искусстве и других областях. Она помогает создавать гармоничные и сбалансированные композиции, которые приятны глазу и воспринимаются как эстетически приятные.

Алгебраическая симметрия

Одним из основных примеров алгебраической симметрии является симметрия функций. Функция считается симметричной относительно оси, если ее график остается неизменным при отражении относительно этой оси. Например, функция f(x) = x^2 является симметричной относительно вертикальной оси.

Другой пример алгебраической симметрии — симметричные матрицы. Квадратная матрица считается симметричной, если она равна своей транспонированной матрице. Это означает, что элементы матрицы отражены относительно главной диагонали. Например, матрица A = [1 2; 2 3] является симметричной.

Алгебраическая симметрия играет важную роль во многих областях математики и физики. Она помогает упростить вычисления и анализ математических моделей, а также находит применение в решении различных задач.

Вопрос-ответ:

Что такое симметрия в математике?

Симметрия — это особое свойство фигур, объектов или функций, при котором они остаются неизменными при некоторых преобразованиях, таких как отражение, поворот или сдвиг.

Какие бывают виды симметрии в математике?

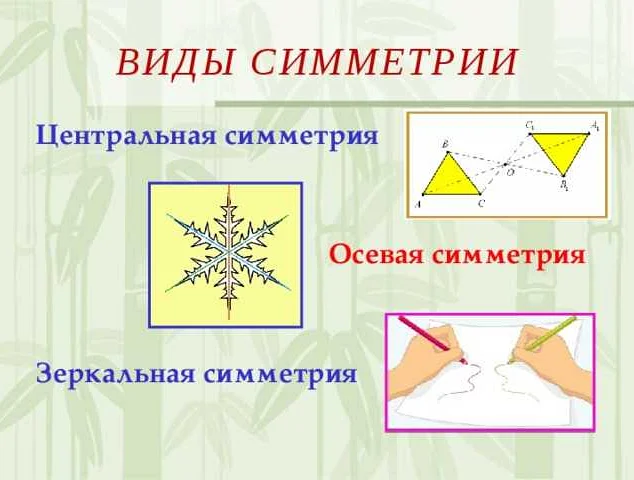
В математике существуют три основных вида симметрии: отражательная (симметрия относительно прямой или плоскости), поворотная (симметрия относительно точки) и трансляционная (симметрия относительно сдвига).

Какие примеры симметричных фигур в математике?

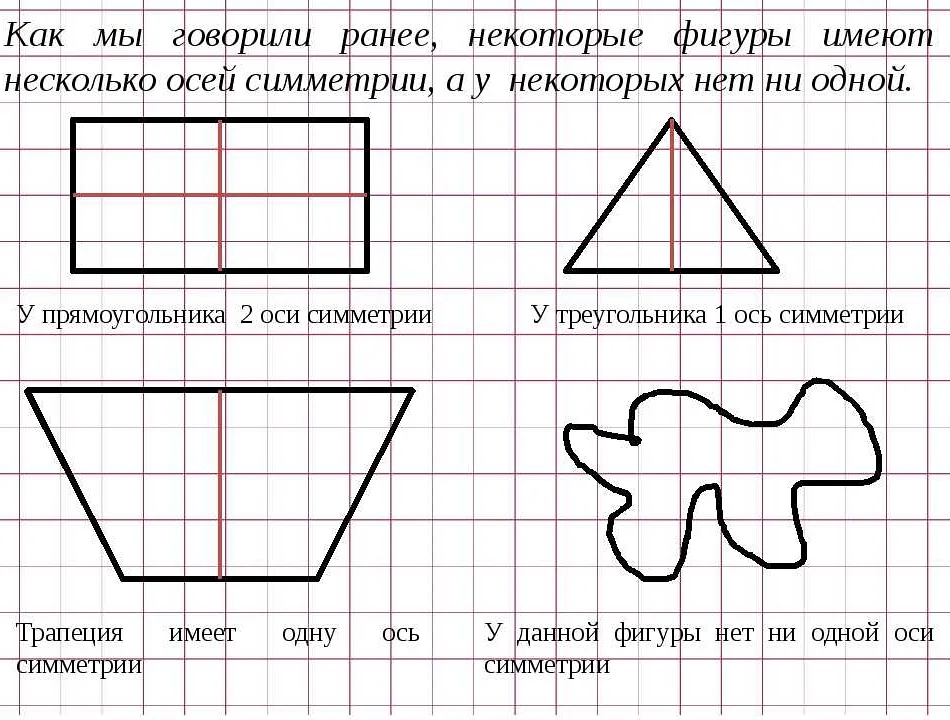
Примерами симметричных фигур могут служить круг, равносторонний треугольник, прямоугольник, квадрат и многоугольники, которые можно разделить на две равные части относительно оси симметрии.

Можно ли найти симметрию в природе или искусстве?

Да, симметрия встречается во многих объектах и явлениях природы, таких как кристаллы, раковины, снежинки. Также симметрия играет важную роль в искусстве, архитектуре и дизайне, где ее используют для создания гармоничных и привлекательных композиций.

Симметрия в природе

Одним из наиболее заметных примеров симметрии в природе является симметрия вокруг оси. Многие растения и животные обладают радиальной симметрией, где они могут быть разделены на две или более одинаковых половинок, относительно оси. Примеры включают цветы, морские звезды и раковины.

Другой пример симметрии в природе — билатеральная симметрия. Это тип симметрии, при котором объект может быть разделен на две одинаковые половины, относительно вертикальной оси. Многие животные, включая насекомых, рыб и млекопитающих, обладают билатеральной симметрией. Это также относится к многим частям тела животных, таким как крылья у птиц или плавники у рыб.

Симметрия в природе также проявляется в фракталах. Фракталы — это геометрические фигуры, которые могут быть разделены на более мелкие части, которые являются похожими на оригинал. Многие природные объекты, такие как облака, горы или деревья, могут быть представлены в виде фракталов. Это свидетельствует о том, что симметрия присутствует не только на макроуровне, но и на микроуровне природы.

Симметрия в природе имеет не только эстетическую ценность, но и функциональное значение. Она помогает организмам адаптироваться к окружающей среде, обеспечивая эффективность и гармонию. Изучение симметрии в природе позволяет лучше понять законы природы и использовать их в нашу пользу.

Симметрия в искусстве

В живописи симметрия часто используется для создания симметричных композиций, где элементы изображения располагаются симметрично относительно центральной оси. Это может создавать ощущение равновесия и стабильности.

Симметрия также часто применяется в архитектуре. Многие здания имеют симметричные фасады, где элементы зеркально повторяются относительно вертикальной оси. Это может придавать зданию величественность и упорядоченность.

В музыке симметрия может быть использована для создания мелодических и ритмических схем, которые зеркально повторяются. Это может придавать музыке гармоничность и согласованность.

Симметрия также может быть использована в скульптуре, дизайне одежды, фотографии и других формах искусства. Она непременно привлекает внимание зрителя и создает особую эстетическую привлекательность.

Использование симметрии в искусстве позволяет подчеркнуть красоту и гармонию форм, создать эффект стабильности и уравновешенности. Это один из способов, которыми художники и дизайнеры могут создавать впечатляющие и привлекательные произведения искусства.

Симметрия в архитектуре

В архитектуре симметрия может быть горизонтальной, вертикальной или осевой. Горизонтальная симметрия предполагает равенство и симметричное расположение элементов относительно горизонтальной оси, что придает зданию стабильность и покой. Вертикальная симметрия подразумевает симметричное расположение элементов относительно вертикальной оси и придает зданию величественность и силу. Осевая симметрия является комбинацией горизонтальной и вертикальной, и создает баланс и симметрию как в плане, так и в фасаде сооружения.

Примеры симметрии в архитектуре включают церкви, дворцы, соборы, музеи и другие исторические и современные сооружения. Классическая архитектура Греции и Рима является одним из наиболее известных и обширно используемых примеров симметрии в архитектуре. Фасады зданий, колоннады, арки и другие декоративные элементы отличаются строгостью и симметрией, создавая впечатление пропорциональности и гармонии.

Симметрия в архитектуре также может быть использована для создания определенного эффекта или эмоционального воздействия на зрителя. Например, равномерное распределение окон на фасаде здания может создать ощущение гостеприимства и открытости, в то время как симметричное расположение колонн может придать зданию величественность и солидность.

Симметрия в архитектуре играет важную роль не только с эстетической точки зрения, но и с практической. Она помогает создать устойчивую и прочную конструкцию, обеспечивает логичное и удобное размещение помещений, а также способствует созданию гармоничного пространства, которое приятно воспринимать и использовать.

Симметрия в музыке

Симметрия может быть горизонтальной или вертикальной. Горизонтальная симметрия в музыке означает, что мелодия или мотив можно разделить на две равные части, которые звучат одинаково или очень похоже. Вертикальная симметрия относится к гармонии и аккордам. Например, аккорды, составленные из одинаковых интервалов, могут создавать ощущение симметрии.

Симметрия также может быть использована в структуре музыкального произведения. Некоторые композиторы используют симметричные формы, такие как соната или фуга, чтобы создать организованное и сбалансированное произведение. Симметрия может помочь слушателю лучше понять структуру и логику музыки.

Симметрия в музыке может быть идеальной или неполной. В идеальной симметрии, две или более части музыкального произведения создают точное зеркальное отражение друг друга. В неполной симметрии, некоторые элементы могут быть изменены или изменены, чтобы создать интересные и неожиданные эффекты.

Симметрия в музыке может вызывать разные эмоции и настроения. Она может быть использована для создания ощущения умиротворения или напряжения. Симметричные музыкальные структуры могут быть узнаваемыми и привлекательными для слушателя.

В целом, симметрия в музыке является важным аспектом композиционного процесса и может быть использована для создания уникальных и запоминающихся музыкальных произведений.

Симметрия в технологиях

Одним из примеров симметрии в технологиях являются симметричные дизайны в архитектуре. Многие здания и сооружения строятся с использованием симметричных форм и элементов. Это позволяет не только создать гармоничный облик, но и повысить прочность и устойчивость конструкции.

Симметрия также применяется в дизайне интерфейсов программного обеспечения. Кнопки, элементы управления и различные элементы интерфейса часто размещаются с использованием симметричных композиций. Это позволяет упростить восприятие информации пользователем и улучшить удобство использования программы.

В технологии производства автомобилей симметрия также играет важную роль. Многие автомобили имеют симметричную форму кузова, что помогает улучшить аэродинамические характеристики и обеспечить более устойчивое движение на дороге.

Архитектурный объект с симметричной формой	Интерфейс программного обеспечения с симметричными элементами	Автомобиль с симметричной формой кузова

Таким образом, симметрия играет важную роль в технологиях, помогая создавать продукты с эстетическими и функциональными преимуществами.