Что такое система координат в математике

Система координат в математике — это упорядоченный набор чисел, используемых для определения точки в пространстве. Она позволяет задавать положение, направление и расстояние между объектами в математической модели. Узнайте, как работает система координат и как она применяется в различных областях науки и техники.

Система координат — это математический инструмент, который позволяет представить и изучать геометрические объекты и их взаимное расположение в пространстве. С помощью системы координат можно определить положение точки, задать направление вектора или построить график функции.

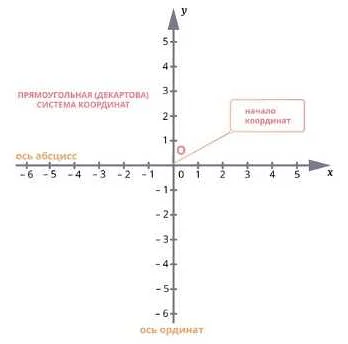
Одна из самых распространенных систем координат — прямоугольная система координат, которая состоит из двух перпендикулярных осей, обычно называемых осью X и осью Y. Ось X горизонтальна и направлена вправо, а ось Y вертикальна и направлена вверх. Нулевая точка, где пересекаются оси X и Y, называется началом координат.

Каждая точка в прямоугольной системе координат имеет свои координаты, которые обозначаются числами в виде упорядоченной пары (X, Y). Первое число — это координата X и указывает положение точки относительно оси X. Второе число — это координата Y и указывает положение точки относительно оси Y.

Система координат является важным инструментом для решения математических задач в различных областях науки и техники. Она позволяет удобно представлять и анализировать данные, проводить геометрические вычисления и визуализировать информацию. Понимание основных понятий и принципов системы координат является необходимым для работы с математикой и ее приложениями.

Система координат: что это такое?

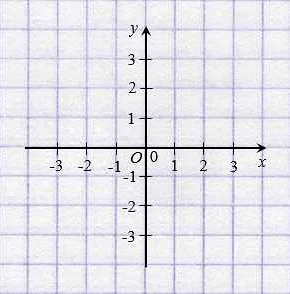
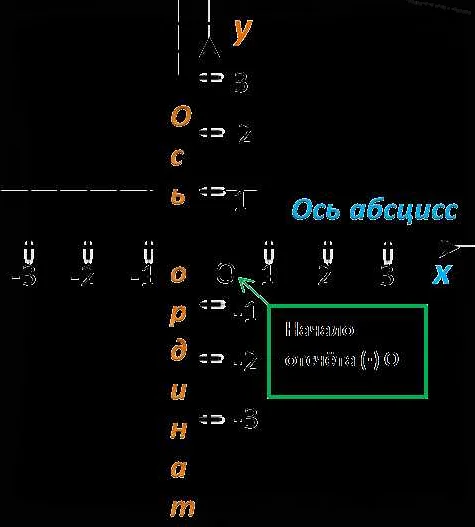
В системе координат каждая ось имеет свою начальную точку, которая называется началом координат. Обычно точка начала координат обозначается буквой O. Абсцисса и ордината точки определяются как расстояния от точки до соответствующих осей. Абсцисса измеряется по горизонтали, а ордината — по вертикали.

Система координат широко применяется в математике, физике, геометрии и других науках для решения различных задач. Она позволяет удобно описывать положение объектов в пространстве или на плоскости, а также производить различные вычисления с их координатами.

Координаты точек: основные понятия

В системе координат точки пространства и плоскости описываются с помощью координат. Координаты точки определяют ее положение относительно начала координат и осей системы.

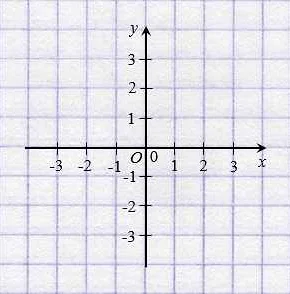
В двумерной системе координат точка определяется двумя числами (x, y), где x — координата точки по горизонтальной оси (ось абсцисс), а y — координата точки по вертикальной оси (ось ординат).

В трехмерной системе координат точка определяется тремя числами (x, y, z), где x — координата точки по горизонтальной оси, y — координата точки по вертикальной оси, а z — координата точки по оси глубины (ось аппликат).

Координаты точек могут быть положительными или отрицательными, в зависимости от их относительного положения относительно начала координат.

Координатная ось обычно имеет масштаб, который позволяет определить, насколько единиц длины на оси соответствует единице длины в реальном мире.

Координаты точек могут быть использованы для определения расстояния между точками, угла между векторами и других геометрических характеристик объектов.

Декартова система координат

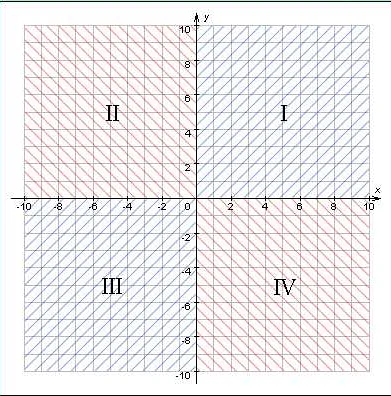
В декартовой системе координат пространство разбивается на оси, которые пересекаются в точке, называемой началом координат. Обычно оси называются x, y и z для двумерного и трехмерного пространства соответственно. Ось x горизонтальная, ось y вертикальная, а ось z направлена вдоль глубины.

Каждая точка в пространстве имеет свои координаты, которые определяют ее положение относительно начала координат. Например, в двумерном пространстве координаты точки могут быть представлены парой чисел (x, y), где x – это расстояние точки от начала координат по горизонтальной оси, а y – по вертикальной оси.

В трехмерном пространстве координаты точки представляются тройкой чисел (x, y, z), где x, y и z – это расстояния точки от начала координат по соответствующим осям.

Декартова система координат широко используется в математике, физике, графике и других науках для описания и анализа объектов и явлений в пространстве.

Полярная система координат

В полярной системе координат точка задается двумя числами: углом и радиусом. Угол измеряется относительно положительного направления оси x и может быть выражен в градусах или радианах. Радиус определяет расстояние от начала координат до точки.

Полярная система координат может быть полезна в случаях, когда точка движется по окружности или когда угол задает направление, а радиус — расстояние.

Таблица ниже показывает некоторые примеры точек в полярной системе координат:

Угол (в градусах)Радиус

0	2
45	3
90	1
180	4

На рисунке ниже показан пример полярной системы координат:

Полярная система координат широко используется в физике, геометрии, аэродинамике и других областях науки и инженерии.

Цилиндрическая система координат

Радиус (r) представляет собой расстояние от начала координат до точки в плоскости xy. Азимут (θ) измеряется в радианах и определяет угол между положительным направлением оси x и лучом, соединяющим начало координат с точкой. Высота (z) указывает на расстояние от плоскости xy до точки.

Для задания точки в цилиндрической системе координат используется следующий порядок записи: (r, θ, z). Например, точка P с радиусом 3, азимутом π/4 и высотой 2 будет записана как P(3, π/4, 2).

Цилиндрическая система координат удобна для описания объектов, имеющих цилиндрическую форму или симметрию вокруг оси z. Она широко применяется в различных областях, включая физику, инженерию и математику.

Сферическая система координат

Радиус (r) представляет собой расстояние от начала координат до точки. Он может быть положительным или нулевым, но не может быть отрицательным. Полярный угол (θ) измеряет угол между положительным направлением оси z и линией, соединяющей начало координат и точку. Азимутальный угол (φ) измеряет угол между положительным направлением оси x и проекцией линии, соединяющей начало координат и точку, на плоскость xy.

Сферическая система координат может быть полезной при описании точек на поверхности Земли, а также в космических и астрономических исследованиях. Она позволяет более удобным образом задавать положение точек в пространстве, особенно если они находятся на больших расстояниях.

Преобразование между сферическими и декартовыми координатами может быть осуществлено с помощью следующих формул:

• x = r * sin(θ) * cos(φ)
• y = r * sin(θ) * sin(φ)
• z = r * cos(θ)

Где x, y, z — декартовы координаты точки, r — радиус, θ — полярный угол, φ — азимутальный угол.

Сферическая система координат является одной из основных систем координат в математике и находит применение в различных областях, таких как физика, геодезия, астрономия и другие.

Преобразование координат

Существуют различные методы преобразования координат, включая:

• Трансляция — это перемещение системы координат вдоль осей без изменения их направления. В этом случае все точки сдвигаются на одно и то же значение по каждой оси.
• Масштабирование — это изменение масштаба системы координат, увеличение или уменьшение расстояний между точками. В этом случае каждая координата умножается на определенный множитель.
• Поворот — это вращение системы координат вокруг точки отсчета на определенный угол. В этом случае координаты каждой точки изменяются согласно формулам для поворота вокруг начала координат.
• Отражение — это отражение системы координат относительно одной или нескольких осей. В этом случае значение координаты изменяется на противоположное.

Преобразование координат является важным инструментом в математике и науке, а также в компьютерной графике и геометрии. Оно позволяет переходить от одной системы координат к другой и упрощает анализ и решение задач в различных областях.

Видео по теме:

Что такое система координат?

Система координат — это метод представления точек в пространстве или на плоскости с помощью числовых значений, называемых координатами. Она состоит из двух осей (горизонтальной и вертикальной) и начала координат, от которого отсчитываются значения координат. Система координат является базовым инструментом для изучения геометрии и алгебры.

В каких областях математики применяется система координат?

Система координат применяется во многих областях математики, включая геометрию, алгебру, анализ, физику и другие естественные науки. Она используется для изучения отношений между объектами, решения уравнений, определения геометрических фигур, анализа функций и многих других задач.

Какие основные понятия входят в систему координат?

Основные понятия в системе координат включают точки, оси, ориентацию осей, отметки и шкалы.