Сколько e в математике
Содержимое
- 1 Сколько e в математике
- 1.1 Число e в математике
- 1.2 Видео по теме:
- 1.3 Определение и значение числа e
- 1.4 Происхождение и история числа e
- 1.5 Вопрос-ответ:
- 1.6 Математические свойства числа e
- 1.7 Применение числа e в математике
- 1.8 Число e в финансовых расчетах
- 1.9 Число e в физике и естественных науках
- 1.10 Число e в компьютерных науках
- 1.11 Число e и его связь с другими постоянными
Узнайте, сколько e в математике и как он используется в различных формулах и уравнениях. Экспонента e является одной из наиболее важных математических констант и находит широкое применение в различных областях науки и инженерии.
Математика, как наука о числах и их взаимоотношениях, постоянно развивается и расширяется. Одним из самых важных и фундаментальных чисел в математике является число e. Несмотря на свою простоту в записи и произношении, число e имеет глубокое значение и обширные применения в различных областях науки и повседневной жизни.
Значение числа e является основой натурального логарифма. Оно приближенно равно 2.71828 и является иррациональным числом. Это означает, что его десятичное представление не имеет периодической или повторяющейся последовательности цифр. Число e является одним из пяти таких чисел, вместе с π, √2, φ и γ.
Использование числа e распространено в различных областях математики, физики, экономики и других наук. Оно находит свое применение в задачах, связанных с ростом и убыванием популяций, процентными ставками, анализом данных, решением дифференциальных уравнений и многих других. Также число e используется в формуле для вычисления сложных процентов и в комплексном анализе.
Число e является фундаментальным и важным для понимания и применения различных математических концепций и теорий. Его значение и использование распространены во многих областях науки и повседневной жизни. Познакомьтесь с числом e и откройте для себя его удивительные свойства и применение!
Число e в математике
Число e было введено Леонардом Эйлером в XVIII веке и названо в честь швейцарского математика Леонарда Эйлера. Оно возникает в различных областях математики, таких как теория вероятностей, математический анализ, дифференциальные уравнения и комплексный анализ.
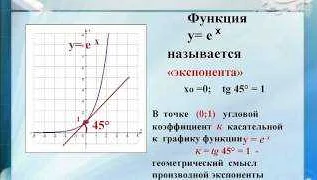
Основное свойство числа e заключается в том, что производная функции e^x равна самой функции e^x. Это свойство делает число e ключевым элементом экспоненциальных функций и логарифмов.
Число e также часто встречается в формуле для вычисления сложного процента. Формула имеет вид A = P(1 + r/n)^(nt), где A – конечная сумма, P – начальная сумма, r – процентная ставка, n – количество периодов в году, t – общее количество периодов. Здесь e возводится в степень, чтобы учесть непрерывное начисление процентов.
В заключение, число e является важной константой в математике и широко используется для моделирования процессов роста и изменения, а также в других областях, связанных с математическим анализом.
Видео по теме:
Определение и значение числа e

Значение числа e приближенно равно 2,718281828459045… Это число является основанием натурального логарифма и имеет множество интересных математических свойств и приложений.
Число e можно представить как сумму бесконечного ряда:
e = 1 + 1/1! + 1/2! + 1/3! + …
где n! обозначает факториал числа n (произведение всех натуральных чисел от 1 до n).
Одно из важнейших свойств числа e заключается в том, что его производная равна самому числу e. То есть, если f(x) = e^x, то f'(x) = e^x.
Интересные приложения числа e включают вычисление сложных процентов, моделирование роста популяции, расчеты с непрерывными процессами и многое другое.
Происхождение и история числа e
История числа e начинается с изучения экспоненциальных функций в математике. Впервые число e появилось в XVII веке благодаря швейцарскому математику Леонарду Эйлеру. Он исследовал ряды, связанные с экспоненциальными функциями и натуральными логарифмами.
Эйлер обратил внимание на особое свойство функции f(x) = (1 + 1/x)^x. При увеличении значения x, функция стремилась к некоторому пределу. Этот предел и был определен Эйлером как число e.
Впоследствии, Эйлер доказал, что e является иррациональным числом, то есть его нельзя представить в виде дроби. Также, он открыл, что число e является основанием натурального логарифма, и имеет множество интересных свойств и приложений.
С течением времени, число e стало широко применяться в разных областях науки. Оно используется в финансовой математике для расчета сложных процентов, в физике для описания процессов роста и распада, в статистике для моделирования вероятности и многих других областях.
Сегодня, число e является одним из фундаментальных математических констант и играет важную роль в развитии науки и технологий.
Вопрос-ответ:
Что такое число e в математике?
Число e – это основа натурального логарифма, которое примерно равно 2.71828. Оно является иррациональным числом, то есть его десятичная запись не повторяется и не может быть выражена обыкновенной дробью.
Какое значение имеет число e?
Число e является фундаментальной константой в математике и имеет множество приложений, особенно в области экспоненциальных функций и дифференциального исчисления. Оно используется для моделирования различных процессов, таких как рост и распад, а также в финансовой математике и теории вероятностей.
Как производится вычисление числа e?
Число e можно приближенно вычислить с помощью формулы e = (1 + 1/n)^n, где n – бесконечно большое число. Чем больше значение n, тем точнее будет приближение. Также число e может быть найдено с использованием ряда Маклорена, который представляет собой бесконечную сумму.
В каких областях науки и техники применяется число e?
Число e широко применяется в физике, экономике, инженерии, компьютерных науках и других областях. Оно используется для моделирования роста популяций, распространения эпидемий, финансовых процессов, электрических цепей и многих других явлений.
Математические свойства числа e
- Производная экспоненты: Производная функции y = e^x равна самой функции, то есть (d/dx)(e^x) = e^x. Это значит, что экспонента имеет свойство сохраняться при дифференцировании.
- Предел при x стремящемся к бесконечности: Предел функции e^x при x стремящемся к бесконечности равен бесконечности, то есть lim(x→∞) e^x = ∞. Это свойство делает число e очень важным при исследовании асимптотического поведения функций.
- Равенство суммы ряда: Число e равно сумме бесконечного ряда 1 + 1/1! + 1/2! + 1/3! + …, где n! обозначает факториал числа n. Это свойство связывает число e с понятием математического ряда и находит применение в различных областях математики.
- Соотношение с натуральным логарифмом: Число e связано с натуральным логарифмом по формуле ln(e) = 1. Это свойство обуславливает выбор числа e в качестве основы логарифмических функций.
- Уникальность: Число e является трансцендентным числом, то есть не является алгебраическим корнем никакого полинома с рациональными коэффициентами. Это свойство делает число e уникальным и отличным от других чисел.
Математические свойства числа e являются основой для многих теорем и формул в различных областях математики, физики и других наук.
Применение числа e в математике
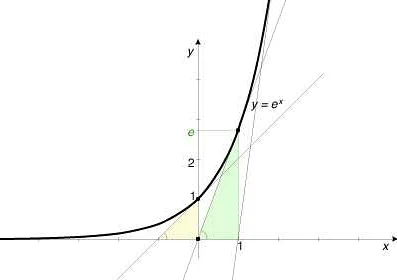
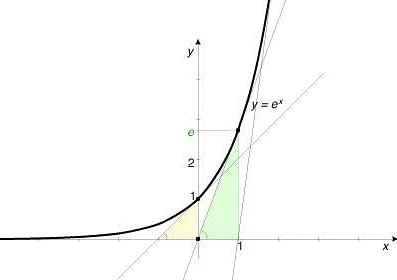
Одним из наиболее известных применений числа e является вычисление экспоненты. Функция экспоненты y = e^x является одной из основных математических функций. Она имеет широкое применение в моделировании роста популяций, распределении вероятностей и в других областях.
Число e также играет важную роль в дифференциальном и интегральном исчислении. Например, производная функции y = e^x равна самой функции, что делает ее особенно удобной при решении дифференциальных уравнений.
В финансовой математике число e используется для расчета сложных процентов. Формула A = P(1 + r/n)^(nt), где A — конечная сумма, P — начальная сумма, r — процентная ставка, n — количество периодов в году, t — общее количество лет, основана на числе e.
Кроме того, число e применяется в статистике, теории информации и теории устойчивости. Оно также является основой для различных математических моделей, которые используются в физике, экономике и других науках.
Область примененияПримеры
| Анализ | Функция экспоненты y = e^x |
| Теория вероятностей | Распределение Пуассона |
| Финансовая математика | Расчет сложных процентов |
| Дифференциальные уравнения | Производная функции y = e^x |
| Статистика | Модель роста популяции |
Применение числа e в математике имеет широкий спектр и является неотъемлемой частью многих математических теорий и моделей. Его уникальные свойства делают его незаменимым инструментом при решении различных задач и проблем. Понимание и использование числа e позволяют математикам и ученым более глубоко и точно анализировать и моделировать реальные явления и процессы.
Число e в финансовых расчетах
В финансовых математических моделях, связанных с процентными ставками, число e используется для вычисления сложных процентов. Сложные проценты представляют собой процентный доход, который начисляется на сумму основного капитала и ранее начисленных процентов.
В финансовых расчетах, число e используется для определения будущей стоимости инвестиций, а также для вычисления эффективной процентной ставки и периода удвоения капитала.
Например, при использовании числа e в формуле для расчета будущей стоимости инвестиций, можно определить, сколько денег будет иметь инвестор после определенного периода времени, учитывая процентную ставку и частоту начисления процентов.
Число e также используется для определения эффективной процентной ставки, которая учитывает не только номинальную процентную ставку, но и частоту начисления процентов. Эффективная процентная ставка позволяет сравнивать различные финансовые инструменты и определить наиболее выгодное вложение средств.
Кроме того, число e используется для вычисления периода удвоения капитала. Период удвоения капитала представляет собой время, за которое вложенный капитал удваивается при заданной процентной ставке и частоте начисления процентов.
Пример расчета будущей стоимости инвестиций
| Начальная сумма инвестиций: | 1000 |
| Процентная ставка: | 5% |
| Частота начисления процентов: | ежемесячно |
| Период времени: | 5 лет |
| Будущая стоимость инвестиций: | 1000 * e^(0.05 * 5) |
Таким образом, число e играет важную роль в финансовых расчетах, позволяя более точно моделировать и прогнозировать различные финансовые сценарии.
Число e в физике и естественных науках
Число e, также известное как число Эйлера, имеет важное значение и в физике и естественных науках. Оно часто встречается в различных математических моделях и уравнениях, которые описывают различные физические явления.
В классической механике, число e возникает при решении дифференциальных уравнений движения. Оно связано с понятием экспоненциального роста или затухания, что позволяет описывать изменение физических величин во времени. Экспоненциальные функции с основанием e являются решениями многих физических уравнений, таких как уравнение диффузии, уравнение теплопроводности и уравнение колебаний.
Число e также играет важную роль в статистической физике и термодинамике. Оно связано с распределением Гиббса и средней энергией системы при равновесии. Понятие энтропии, которое является ключевым в термодинамике, также тесно связано с числом e.
В квантовой механике, число e возникает при решении уравнения Шредингера, которое описывает поведение элементарных частиц и атомов. Оно связано с вероятностным распределением электронов в атоме и волновыми функциями, описывающими их состояния.
Кроме того, число e также используется в различных формулах и уравнениях в других областях естественных наук, таких как оптика, электромагнетизм и гравитация. Оно является одним из фундаментальных математических констант, которые позволяют описывать мир вокруг нас и понимать его законы.
Число e в компьютерных науках

В программировании, число e широко используется в различных областях. Например, в алгоритмах оптимизации и машинном обучении, число e может использоваться для вычисления градиента функции и нахождения минимума или максимума. Оно также может быть использовано для вычисления вероятности и статистических моделей.
Кроме того, число e имеет значение в технической информатике и теории кодирования. Оно используется для вычисления энтропии и сжатия данных, а также в алгоритмах проверки целостности и коррекции ошибок.
Таким образом, число e является основным математическим константой, которая играет важную роль в компьютерных науках. Его значение и применение помогают разработчикам создавать эффективные и точные алгоритмы, а также решать широкий спектр задач в различных областях компьютерных наук.
Число e и его связь с другими постоянными
Число e тесно связано с другими важными математическими постоянными. Например, оно связано с числом π (пи) формулой Эйлера:
e^(iπ) + 1 = 0
Это равенство, называемое формулой Эйлера, объединяет пять ключевых математических констант: e, i (мнимое число), π, 1 и 0. Оно является одним из самых известных и впечатляющих результатов в математике.
Число e также связано с комплексными числами и экспоненциальной функцией. Экспонента с основанием e имеет особое значение, так как ее производная равна самой себе. Это делает число e важным для решения дифференциальных уравнений и моделирования процессов роста и распределения.
Число e появляется во многих областях математики, физики, экономики и других наук. Оно также имеет связь с комплексным анализом, теорией вероятностей и другими разделами математики.
В заключение, число e является ключевой математической постоянной с множеством интересных и полезных свойств. Оно связано с другими постоянными, такими как π, и является основой для многих математических и научных приложений.

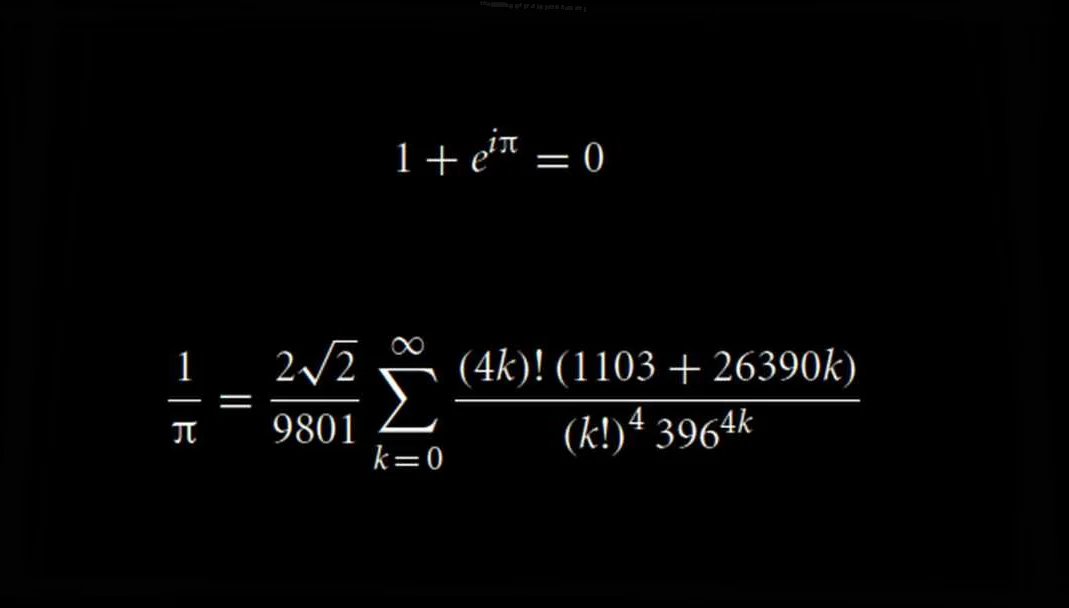

Статья очень интересная и познавательная! Никогда не задумывался о том, сколько e в математике. А оказывается, это такое важное число и имеет множество применений. Я ознакомился с определением числа e и понял, что оно является основой натурального логарифма и экспоненциальной функции. Удивительно, как такое простое число может быть столь значимым в математике и науке в целом. Я также узнал, что число e используется в финансовых расчетах, в моделировании природных процессов и даже в медицине. Вот какое универсальное значение может иметь всего одно число! Спасибо за эту информативную статью, теперь я знаю, насколько важно и полезно знание числа e.