Сколько градусов у развернутого угла в математике
Содержимое
- 1 Сколько градусов у развернутого угла в математике
- 1.1 Что такое угол в математике
- 1.2 Определение угла
- 1.3 Единицы измерения угла
- 1.4 Как определить развернутый угол
- 1.5 Как вычислить градусы развернутого угла
- 1.6 Примеры развернутых углов
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Свойства и особенности развернутых углов
- 1.10 Практическое применение развернутых углов
Развернутый угол в математике имеет 360 градусов. Узнайте, как определить количество градусов у развернутого угла и как использовать его в различных задачах и вычислениях.
Развернутый угол — это один из основных понятий в геометрии. Он представляет собой угол, который равен 360 градусам или 2π радианам. Такой угол получается при полном обороте вокруг точки. Развернутый угол важен для понимания кругового движения и использования тригонометрических функций.
В математике углы измеряются в градусах, минутах и секундах. Градус — это наибольшая единица измерения угла. Он равен 1/360 развернутого угла. В свою очередь, градус делится на 60 минут, а минута — на 60 секунд. Таким образом, развернутый угол составляет 21 600 минут или 1 296 000 секунд.
Развернутый угол имеет множество применений в различных областях науки и техники. Например, он используется в астрономии для измерения долготы и широты небесных объектов. Также развернутый угол применяется в физике для расчета периодических явлений, например, колебаний и волн. Кроме того, в компьютерной графике и анимации развернутый угол используется для создания плавных и реалистичных движений.
В заключение, развернутый угол в математике составляет 360 градусов или 2π радианов. Он играет важную роль в геометрии, тригонометрии, астрономии, физике и компьютерной графике. Знание этого понятия позволяет лучше понимать и анализировать различные процессы, связанные с круговыми движениями и периодическими явлениями.
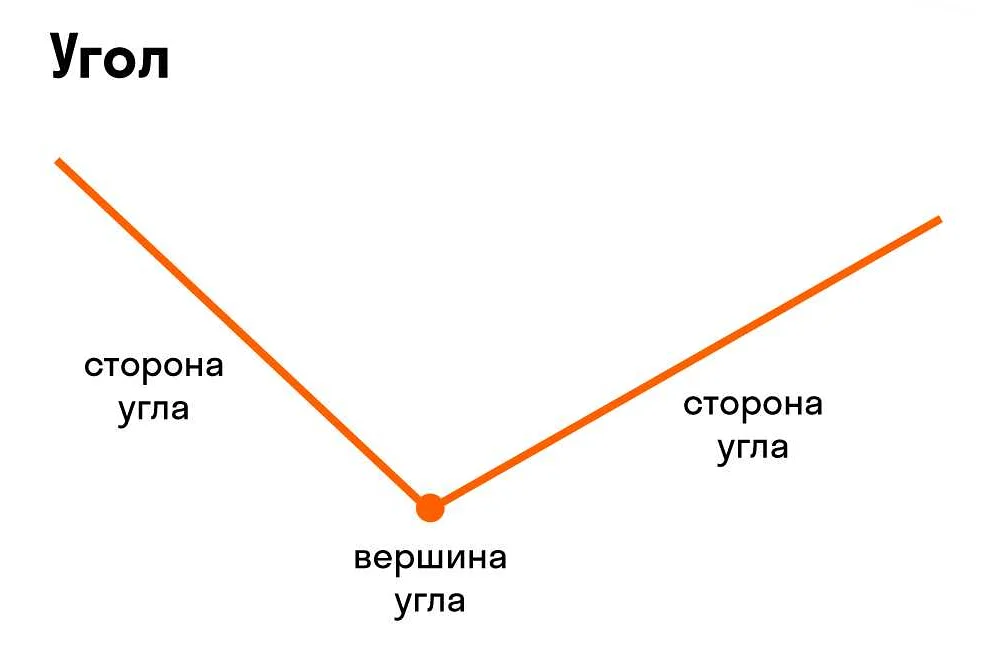
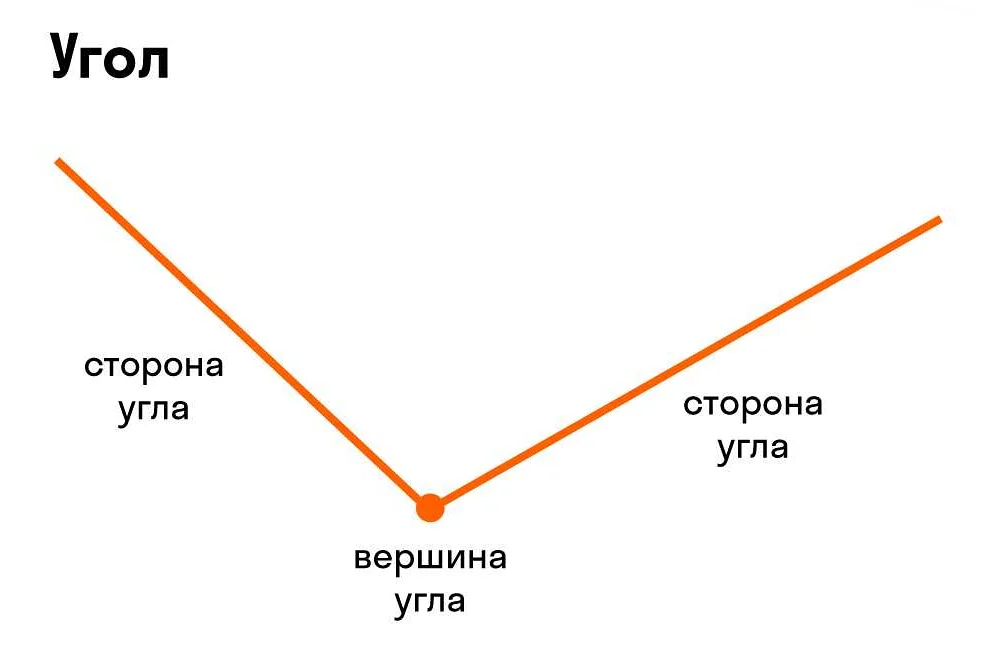
Что такое угол в математике
Угол измеряется в градусах (°), минутах (‘) и секундах («). Один полный оборот составляет 360°. Отклонение от полного оборота может быть как положительным, так и отрицательным.
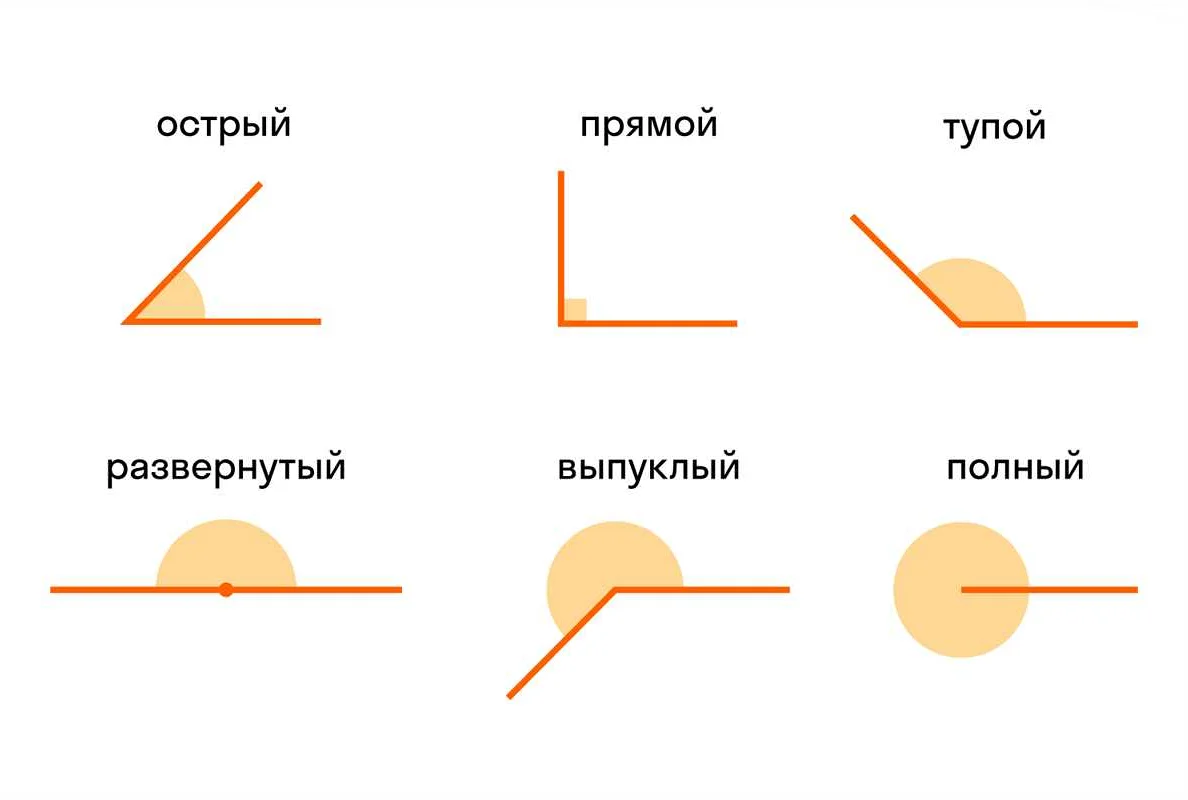
Углы могут быть различными по величине:
- Острый угол — угол, который меньше 90°.
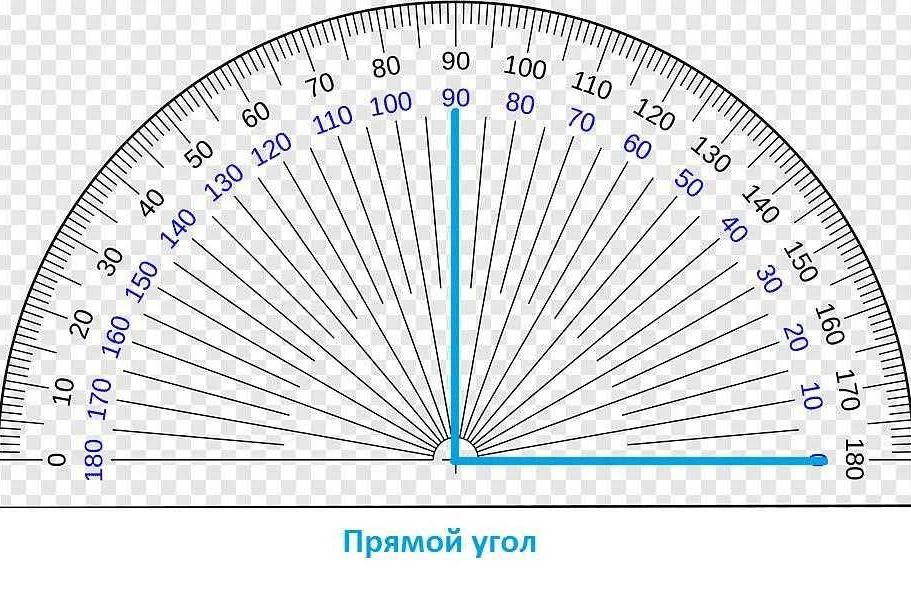
- Прямой угол — угол, равный 90°.
- Тупой угол — угол, который больше 90°, но меньше 180°.
- Развернутый угол — угол, равный 180°.
- Полный угол — угол, равный 360°.
Углы могут быть измерены с использованием различных инструментов, таких как транспортир или гониометр. Знание углов и их свойств является важной частью геометрии и может быть применено во многих областях, включая инженерию, архитектуру, физику и технические науки.
Определение угла
Угол измеряется в градусах, минутах и секундах. Один градус составляет 1/360 часть полного оборота и обозначается символом °. Круговой угол составляет 360 градусов, половинный круг — 180 градусов, а прямой угол — 90 градусов.
Углы могут быть разнообразными: острыми, прямыми, тупыми, полными и отрицательными. Острый угол меньше прямого угла, прямой угол равен 90 градусам, а тупой угол больше прямого угла. Полный угол составляет 360 градусов, а отрицательный угол имеет направление противоположное положительному углу.
Углы широко используются в математике, геометрии, физике и других науках. Они позволяют описывать и измерять повороты, направления и относительные положения объектов и явлений.
Единицы измерения угла
Одно полное вращение — 360 градусов. Таким образом, развернутый угол составляет 360 градусов. Это значит, что при повороте точки вокруг фиксированной точки на 360 градусов, она вернется в исходное положение.
Кроме градуса, в математике существуют и другие единицы измерения угла:
Минута – это единица угла, равная 1/60 градуса. Обозначается символом ′.
Секунда – это единица угла, равная 1/60 минуты или 1/3600 градуса. Обозначается символом ″.
Минуты и секунды используются, когда необходимо более точное измерение угла. Например, для задания координат на сфере или для измерения угловых скоростей в физике.
Важно: при работе с углами необходимо указывать единицы измерения, чтобы избежать путаницы и ошибок.
Как определить развернутый угол
Для определения развернутого угла можно использовать различные методы. Один из самых простых и понятных методов — это использование градусного измерения.
Градус — это единица измерения угла. Полный развернутый угол составляет 360 градусов. При этом, каждая четверть развернутого угла составляет 90 градусов.
Определить развернутый угол можно с помощью специальной таблицы, в которой указаны значения угла в градусах. Ниже приведена таблица, показывающая различные значения угла в градусах:
УголГрадусы
| Четверть разворота | 90 градусов |
| Половина разворота | 180 градусов |
| Три четверти разворота | 270 градусов |
| Полный разворот | 360 градусов |
Таким образом, для определения развернутого угла необходимо знать, что полный развернутый угол составляет 360 градусов, а каждая его четверть — 90 градусов.
Как вычислить градусы развернутого угла
Самый простой способ вычисления градусов развернутого угла — это умножить количество полных оборотов на 360. Например, если угол совершает два полных оборота, то градусы развернутого угла будут равны 2 * 360 = 720 градусов.
Если угол совершает меньше одного полного оборота, то можно использовать пропорцию для определения количества градусов развернутого угла. Например, если угол охватывает 3/4 от полного оборота, то градусы развернутого угла равны (3/4) * 360 = 270 градусов.
Если угол задан в радианах, его можно перевести в градусы, умножив на (180/π). Например, если угол равен π/2 радиан, то его эквивалент в градусах будет (π/2) * (180/π) = 90 градусов.
Также следует помнить, что градусы развернутого угла могут быть отрицательными, если угол совершает обратное вращение. Например, если угол совершает полный оборот против часовой стрелки, то градусы развернутого угла будут равны -360 градусов.
Примеры развернутых углов

Развернутый угол имеет меру 360 градусов. Это значит, что полный оборот вокруг точки составляет 360 градусов.
Несколько примеров развернутых углов:
- Полный оборот: 360 градусов
- Два полуоборота: 720 градусов
- Три полуоборота: 1080 градусов
- Четыре полуоборота: 1440 градусов
Таким образом, развернутый угол может быть представлен любой мерой, кратной 360 градусам. Это позволяет нам измерять углы, превышающие 360 градусов, используя развернутые углы.
Видео по теме:
Вопрос-ответ:
Как определить количество градусов в развернутом угле?
Развернутый угол составляет 360 градусов.
Что такое развернутый угол в математике?
Развернутый угол — это угол, чья мера составляет 360 градусов. Он представляет собой полную окружность.
Как посчитать развернутый угол, если даны меры двух углов?
Если даны меры двух углов, то развернутый угол можно найти, сложив их меры. Например, если один угол имеет меру 120 градусов, а другой — 240 градусов, то развернутый угол будет составлять 360 градусов.
Если развернутый угол составляет 360 градусов, сколько градусов составляют половина развернутого угла?
Половина развернутого угла составляет 180 градусов. Поскольку развернутый угол равен 360 градусам, его половина будет составлять половину от этого числа.
Свойства и особенности развернутых углов

У развернутого угла есть несколько свойств и особенностей:
1. Прямая линия: Развернутый угол изображается в виде прямой линии, которая делит плоскость пополам. Это означает, что все точки на одной стороне прямой линии находятся на одной полуплоскости, а точки на другой стороне — на другой полуплоскости.
2. Измерение угла: Развернутый угол всегда составляет 180 градусов. Это означает, что он полностью поворачивается вокруг точки, образуя полную окружность или полный оборот.
3. Сумма смежных углов: Развернутый угол является суммой двух смежных углов, которые вместе образуют прямую линию. Каждый из этих углов составляет по 90 градусов.
4. Значение синуса, косинуса и тангенса: Развернутый угол имеет определенные значения для синуса, косинуса и тангенса. Синус и тангенс развернутого угла равны нулю, а косинус равен -1.
Развернутый угол имеет важное значение в различных областях математики и физики. Он используется при изучении геометрии, тригонометрии, а также в механике и электричестве. Понимание свойств и особенностей развернутых углов позволяет решать различные задачи и применять их в реальных ситуациях.
Практическое применение развернутых углов

Развернутые углы, также известные как полные углы, имеют важное применение в различных областях жизни и науки. Понимание и умение работать с такими углами необходимо для решения разнообразных задач и выполнения практических заданий.
Одно из практических применений развернутых углов – в геометрии. Развернутый угол составляет 360 градусов, что является максимальным значением угла. Используя эту информацию, можно решать задачи, связанные с измерением, сравнением и построением геометрических фигур. Например, при построении круга необходимо знать, что полный угол вокруг центра составляет 360 градусов.
Еще одним примером практического применения развернутых углов является работа с компасом. Компас используется для определения направления на местности, а основывается на измерении углов. Развернутый угол позволяет удобно и точно определять направление с помощью компаса.
В приложениях и играх, где используется движение или поворот объектов, также применяются развернутые углы. Например, в компьютерных играх, где игрок должен управлять транспортным средством или персонажем, необходимо знать, насколько градусов нужно повернуть объект, чтобы он двигался или смотрел в нужном направлении.
Примеры практического применения развернутых углов:
| Построение круга |
| Определение направления с помощью компаса |
| Управление движением объектов в играх и приложениях |
Понимание и умение работать с развернутыми углами является важным навыком, который может быть применен в различных сферах нашей жизни. Оно позволяет решать задачи, связанные с геометрией, навигацией и программированием, а также развивает логическое мышление и представление о пространстве.
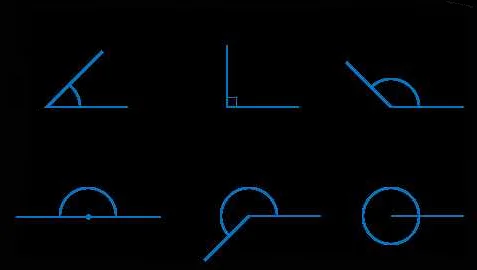

Математика всегда была моей слабой стороной, но однажды я задался вопросом, сколько градусов составляет развернутый угол. Оказывается, развернутый угол — это угол, который полностью охватывает всю окружность. И тут я узнал, что такой угол равен 360 градусам. Вот это да, оказывается, угол может быть таким большим! Мне было интересно, каким образом ученые пришли к такому числу. Исследуя и изучая геометрию, они пришли к выводу, что окружность, состоящая из 360 градусов, наиболее удобна для решения математических задач. Вот такой интересный факт, который я узнал сегодня. Но теперь я хочу узнать, какие еще интересные факты связаны с углами в математике.
Статья очень полезная и информативная. Я всегда задавалась вопросом, сколько градусов составляет развернутый угол в математике. Было интересно узнать, что развернутый угол составляет 360 градусов. Теперь я понимаю, как измеряется угол и как он связан с полным оборотом. Эта информация поможет мне лучше понять геометрию и решать задачи по этой теме. Большое спасибо за статью!
В математике развернутый угол составляет 360 градусов. Это значит, что если мы представим окружность, то развернутый угол будет охватывать все ее точки. Это важно для измерения углов и работы с ними. Например, если нам нужно определить, сколько градусов занимает угол между двумя лучами, мы можем измерить его размер и выразить в градусах. Развернутый угол также помогает в понимании геометрических форм и их свойств. Изучение углов в математике помогает нам лучше понимать и анализировать окружающий мир, а также применять знания в повседневной жизни.
Отличная статья! Всегда хотела узнать, сколько градусов составляет развернутый угол в математике. Было интересно узнать, что развернутый угол составляет 360 градусов. Это значит, что если я возьму прямой угол и разверну его полностью, то получу 360 градусов. Теперь я понимаю, что вся окружность также состоит из 360 градусов. Это очень полезная информация, которая поможет мне лучше понимать геометрию и работать с углами. Спасибо за разъяснение! Жду с нетерпением новых интересных статей!