Математика сколько градусов содержит угол который составляет

В математике угол, который составляет, может содержать различное количество градусов. Угол может быть остроугольным, прямым, тупоугольным или полным, и количество градусов в нем зависит от его вида.

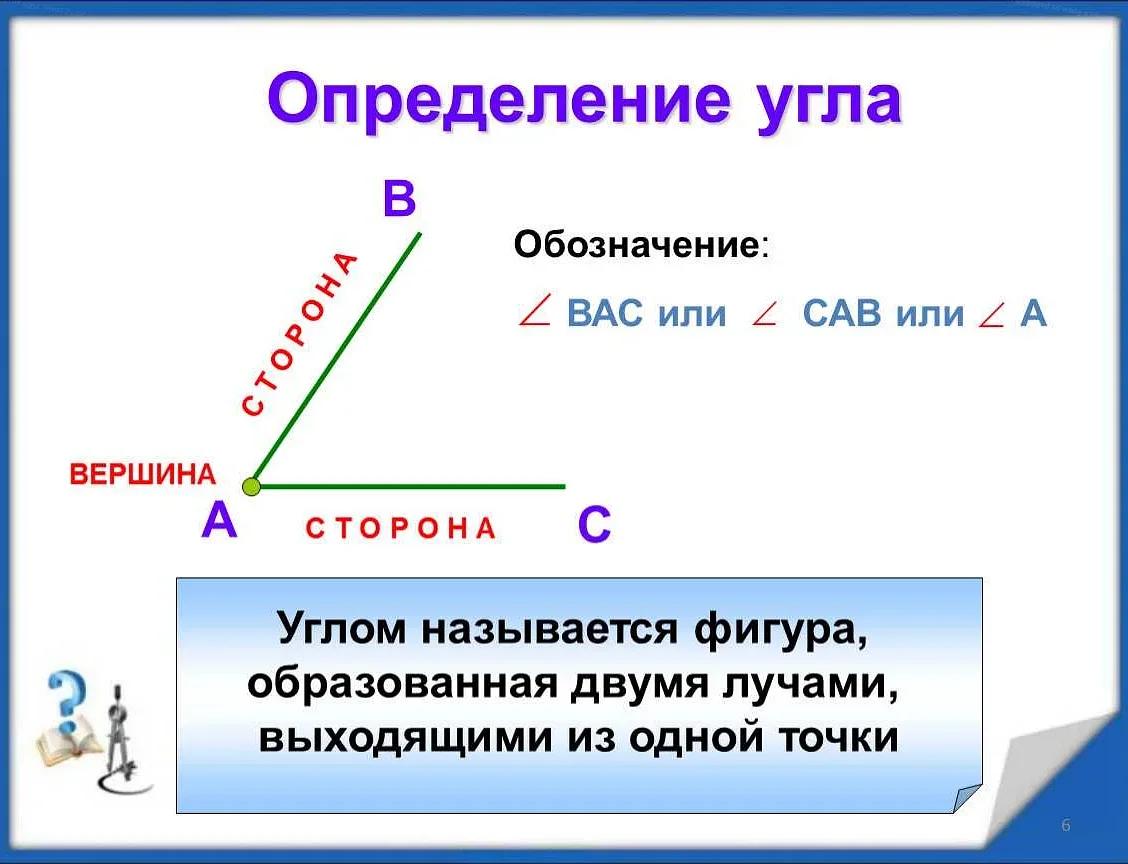
Угол — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки, которая называется вершиной. В математике углы измеряются в градусах. Сколько градусов содержит угол, зависит от его величины.

Градус — это единица измерения углов, которая равна 1/360 части полного оборота. Таким образом, полный оборот составляет 360 градусов. Углы меньше полного оборота могут быть как острыми (меньше 90 градусов), так и тупыми (больше 90 градусов).

Острые углы могут быть различных размеров. Например, прямой угол составляет 90 градусов, а угол между двумя прямыми линиями, называемый вертикальным углом, также равен 90 градусам. Меньшие острые углы могут быть измерены в десятых или сотых долях градуса.

Тупой угол имеет величину больше 90 градусов. Например, угол прямого треугольника составляет 180 градусов, а тупой угол, равный 270 градусам, называется рефлексным углом. Углы, превышающие 360 градусов, считаются смежными с нулевым углом и могут быть измерены в отрицательных числах.

Итак, количество градусов, содержащихся в угле, зависит от его величины и может быть любым числом в диапазоне от 0 до 360 градусов, включая эти значения. Знание величины угла позволяет нам оценивать и сравнивать различные геометрические фигуры и рассчитывать их свойства.

Математика: углы и их измерение

Измерение углов происходит в градусах. Градусы — это единицы измерения для углов. Величина угла измеряется с использованием полного круга, который делится на 360 равных частей. Каждая часть называется градусом.

Углы могут быть измерены с помощью различных инструментов, таких как геометрический транспортир или специальные угломеры. Транспортир представляет собой полукруглый инструмент с градусной шкалой, который позволяет точно измерять углы. Угломеры — инструменты, которые позволяют измерять углы с большей точностью и могут использоваться в различных областях, таких как строительство и инженерия.

Важно помнить, что сумма углов в треугольнике равна 180 градусам, а сумма углов в четырехугольнике равна 360 градусам. Изучение углов и их измерение имеют важное значение в различных областях науки и практического применения, таких как геометрия, физика и архитектура.

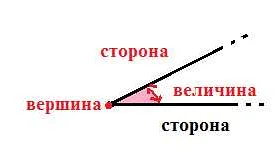
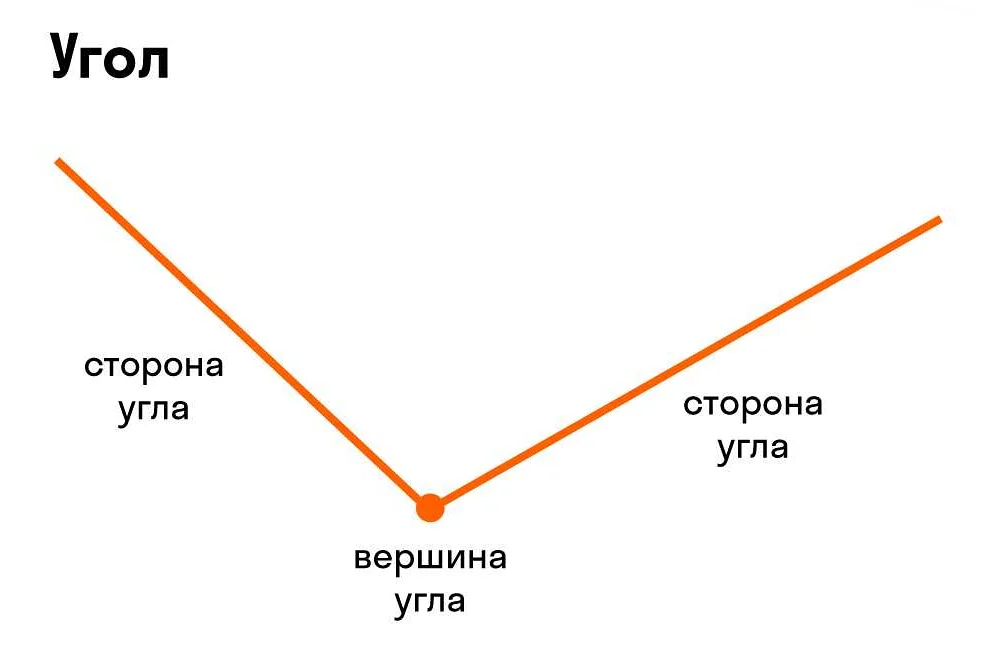
Определение угла и его составляющих

Угол состоит из следующих составляющих:

СоставляющаяОписание

Вершина угла	Точка, из которой исходят два луча, образующих угол.
Начальная сторона	Первый из двух лучей, образующих угол. Он обычно обозначается символом «AB».
Конечная сторона	Второй из двух лучей, образующих угол. Он обычно обозначается символом «AC».

Угол измеряется с помощью транспортира или специального инструмента, называемого градусником. Один полный оборот градусника составляет 360°. Углы могут быть острыми, прямыми, тупыми или полными в зависимости от своего размера.

Градусы: основная единица измерения углов

Градус обозначается символом ° и равен 1/360 полного оборота. Таким образом, полный оборот составляет 360 градусов.

Градусы применяются в различных областях, включая геометрию, физику, астрономию и инженерные науки. Они используются для измерения углов между линиями, плоскостями или поверхностями.

Для более точного измерения углов можно использовать минуты и секунды, которые являются дополнительными единицами измерения. 1 градус равен 60 минутам, а 1 минута равна 60 секундам.

Единица измеренияОбозначениеОтношение к градусу

Градус	°	1
Минута	‘	1/60
Секунда	»	1/3600

Градусы обладают свойствами, позволяющими выполнять операции с углами, такие как сложение, вычитание, умножение и деление. Они также используются для определения тригонометрических функций, таких как синус, косинус и тангенс.

Изучение градусов и их применение в математике позволяет лучше понять и анализировать углы и их свойства, что важно для решения множества задач и проблем, возникающих в различных областях науки и техники.

Прямой угол: сколько градусов содержит прямой угол?

90 градусов — это четверть полного оборота вокруг точки. Когда мы измеряем углы, мы используем градусную меру, которая разбивает полный оборот на 360 градусов. Прямой угол занимает четверть этой меры и является самым большим углом среди прямоугольных углов.

Прямой угол также имеет много важных свойств и применений в геометрии. Он является основой для определения других типов углов, таких как острый угол (меньше 90 градусов) и тупой угол (больше 90 градусов). Прямой угол также используется в различных формулах и теоремах, связанных с треугольниками и прямоугольниками.

Важно помнить, что прямой угол всегда равен 90 градусам, независимо от его размера и формы. Это основное свойство, которое позволяет нам использовать его в различных математических расчетах и конструкциях.

Острый угол: сколько градусов содержит острый угол?

• Острый угол всегда меньше прямого угла (90 градусов).
• Если сумма двух острых углов равна 90 градусов, то такие углы называются смежными.
• В треугольнике острый угол обозначается буквой A.
• Острый угол может быть измерен с помощью геометрических инструментов, таких как угломер.

Обычно острый угол измеряется в градусах. Например, угол размером 45 градусов является острым углом. Острый угол также может быть измерен в радианах, где 1 радиан равен примерно 57,3 градуса. Однако, для большинства практических задач используется градусная мера острого угла.

Тупой угол: сколько градусов содержит тупой угол?

Точная мера тупого угла может быть различной в зависимости от его величины. Например, угол в 100 градусов является тупым углом, так как он больше 90 градусов, но меньше 180 градусов.

Мера тупого угла может быть выражена в градусах, минутах и секундах, так же, как и другие углы. Например, тупой угол в 120 градусов может быть записан как 120°, или 120 градусов, или 120° 00′ 00″.

Тупые углы встречаются в различных геометрических фигурах, таких как треугольники или многоугольники. Изучение тупых углов позволяет лучше понять и анализировать формы и свойства этих фигур.

Смежные углы: как определить количество градусов в смежных углах?

Чтобы определить количество градусов в смежных углах, можно воспользоваться следующим правилом:

Если один из углов измеряет n градусов, то второй угол будет иметь (180 — n) градусов.

Например, если один из смежных углов составляет 60°, то другой угол будет составлять (180 — 60) = 120°.

Также стоит отметить, что смежные углы могут быть как прямыми (90°), так и тупыми (больше 90°), а также острыми (меньше 90°).

Зная количество градусов в одном из смежных углов, можно легко определить количество градусов в другом угле и решать задачи, связанные с смежными углами.

Вертикальные углы: сколько градусов содержат вертикальные углы?

По определению, сумма мер двух вертикальных углов составляет 180 градусов. Это означает, что если один вертикальный угол имеет меру 60 градусов, то второй вертикальный угол будет иметь меру 120 градусов. Если первый угол равен 90 градусам, то второй угол также будет равен 90 градусам.

Вертикальные углы имеют важное значение в геометрии и могут использоваться для решения различных задач. Например, если известна мера одного вертикального угла, то можно найти меру другого угла. Также, зная меру одного вертикального угла, можно определить меру угла, образованного пересекающимися прямыми.

Изучение вертикальных углов позволяет лучше понять геометрию и решать задачи, связанные с углами и прямыми линиями.

Вопрос-ответ:

Как посчитать количество градусов в угле?

Чтобы посчитать количество градусов в угле, необходимо знать его вид. Если угол прямой (90 градусов), то ответ уже известен. Если же угол не является прямым, то для его измерения необходимо использовать инструменты, такие как транспортир или градусник.

Можно ли измерить угол без специальных инструментов?

Да, угол можно примерно измерить без специальных инструментов, используя приближенные значения. Например, можно сравнить угол с известным углом, который составляет 90 градусов (прямой угол) или 180 градусов (полный оборот). Таким образом, можно оценить, больше или меньше этих значений угол, который нужно измерить.

Можно ли измерить угол с помощью смартфона?

Да, с помощью смартфона можно измерить угол. Существуют специальные приложения, которые используют акселерометр и гироскоп смартфона для измерения углов. Эти приложения позволяют точно определить угол, который составляет объект или поверхность относительно горизонтали или вертикали.

Какая разница между градусами и радианами в измерении углов?

Градусы и радианы — это две разные единицы измерения углов. Градусы — это наиболее распространенная единица, которая используется в повседневной жизни. Одна полная окружность равна 360 градусам. Радианы же — это единица измерения, используемая в математике и физике. В радианной системе одна полная окружность равна 2π радиан. Для преобразования углов из градусов в радианы необходимо умножить значение на π/180, а для преобразования из радианов в градусы — умножить на 180/π.

Сумма углов в треугольнике: сколько градусов составляют углы в треугольнике?

Каждый угол в треугольнике имеет свое значение в градусах. В равностороннем треугольнике все три угла равны между собой и составляют по 60 градусов каждый. В прямоугольном треугольнике один из углов равен 90 градусам, а остальные два угла дополняют его до 180 градусов.

Если треугольник не является равносторонним или прямоугольным, то углы могут иметь разные значения. Но в любом случае, сумма углов в треугольнике всегда будет равна 180 градусам.

Зная сумму углов в треугольнике, мы можем вычислить значение каждого угла при условии, что известно значение хотя бы двух углов.

Таким образом, сумма углов в треугольнике является важным свойством этой геометрической фигуры и позволяет нам рассчитывать значения углов в треугольнике при известных данных.

Видео по теме: