Треугольные числа что это в математике

Треугольные числа — это числовая последовательность, в которой каждое число представляет собой сумму всех натуральных чисел до него. Это концепция из области математики, которая имеет множество применений в различных областях, включая комбинаторику, криптографию и программирование. Узнайте больше о треугольных числах и их свойствах в этой статье.

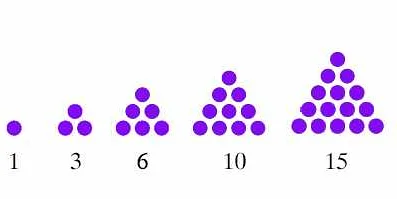
Треугольные числа – это последовательность чисел, которая получается путем суммирования натуральных чисел от 1 до n. Треугольные числа получили свое название благодаря тому, что можно представить их в виде треугольной формы. Это уникальное свойство делает их особенно интересными для математиков и исследователей.

Одним из примеров треугольных чисел является последовательность 1, 3, 6, 10, 15 и т.д. Если внимательно посмотреть на эти числа, можно заметить, что каждое следующее число получается путем прибавления к предыдущему числу следующего натурального числа. Например, число 6 получается путем сложения чисел 1, 2 и 3.

Треугольные числа широко применяются в математике и других науках. Они используются для решения различных задач, включая комбинаторику, геометрию и даже в криптографии. Например, треугольные числа помогают в решении задач о количестве различных путей в сетке или количество диагоналей в многоугольнике.

Треугольные числа также имеют свои интересные свойства. Например, они могут быть представлены в виде произведения двух последовательных натуральных чисел, что делает их еще более удивительными.

Исследование треугольных чисел позволяет математикам расширять свои знания и разрабатывать новые методы и алгоритмы. Они помогают увидеть закономерности и шаблоны в числах и решать сложные задачи. Поэтому изучение треугольных чисел имеет большое значение для развития математики и других наук.

Треугольные числа: основные понятия и свойства

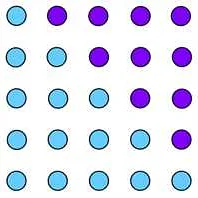
Tn = 1 + 2 + 3 + … + n = n(n+1)/2

Треугольные числа получаются путем добавления следующего натурального числа к предыдущей сумме. Например, первые несколько треугольных чисел выглядят так:

T1 = 1

T2 = 1 + 2 = 3

T3 = 1 + 2 + 3 = 6

T4 = 1 + 2 + 3 + 4 = 10

Треугольные числа имеют несколько интересных свойств:

1. Любое число можно представить в виде суммы двух треугольных чисел. Например, число 10 можно представить в виде 6 + 4 = 10.

2. Треугольные числа образуют арифметическую прогрессию. Разница между последовательными треугольными числами всегда равна следующему натуральному числу. Например, разница между 6 и 3 равна 4, а разница между 10 и 6 равна 5.

3. Каждое треугольное число имеет целочисленный корень. Например, квадратный корень из 6 равен 2, а квадратный корень из 10 равен 3.

Треугольные числа используются в различных областях математики, физики и информатики. Они помогают решать задачи, связанные с комбинаторикой, геометрией и алгеброй. Кроме того, треугольные числа являются основой для формирования других последовательностей и числовых фигур, таких как пирамиды и треугольные матрицы.

Видео по теме:

Что такое треугольные числа?

Треугольные числа получили свое название из-за своей геометрической интерпретации. Можно представить треугольные числа в виде размещения точек в форме треугольника. Например, первое треугольное число 1 можно представить как одну точку. Второе треугольное число 3 можно представить как треугольник с одной точкой в верху и двумя точками внизу. Третье треугольное число 6 будет уже представляться треугольником с одной точкой вверху, двумя точками в середине и тремя точками внизу, и так далее.

Треугольные числа имеют много интересных математических свойств и используются в различных областях. Они могут быть использованы для решения задач комбинаторики, а также в различных алгоритмах и формулах. Например, треугольные числа встречаются при рассмотрении суммы всех натуральных чисел, квадратов натуральных чисел и других последовательностей.

Изучение треугольных чисел позволяет лучше понять связь между арифметикой и геометрией, а также обнаружить регулярности и закономерности в математических последовательностях.

Формула для вычисления треугольных чисел

Треугольные числа можно вычислить с помощью простой формулы. Для любого положительного целого числа n, n-е треугольное число можно найти с помощью формулы:

Tn = n * (n + 1) / 2

Где Tn представляет собой n-е треугольное число. Например, первое треугольное число (T1) равно 1, второе (T2) равно 3, третье (T3) равно 6 и так далее.

Формула для вычисления треугольных чисел основывается на том факте, что каждое треугольное число можно представить в виде треугольной формы, где количество элементов в каждом ряду равно номеру этого ряда. Например, первый ряд состоит из одного элемента, второй ряд — из двух элементов, третий ряд — из трех элементов и так далее.

Использование данной формулы позволяет вычислить треугольные числа для любого положительного целого числа n, что может быть полезно в различных математических задачах и алгоритмах.

Связь треугольных чисел с геометрией

Связь между треугольными числами и геометрией становится ясной при рассмотрении способа их генерации. Одно из распространенных определений треугольных чисел — это сумма натуральных чисел от 1 до n, где n — номер треугольного числа. Таким образом, каждое треугольное число представляет собой сумму точек, расположенных на каждой стороне треугольника.

Треугольные числа также имеют интересные свойства, связанные с геометрией. Например, сумма всех треугольных чисел равна квадрату последнего числа. Это свойство можно объяснить с помощью геометрического представления треугольных чисел, где каждое число представляет собой точку внутри треугольника. При сложении треугольных чисел, точки с одинаковыми координатами образуют квадраты, а сумма всех точек внутри треугольника равна квадрату последнего числа.

Таким образом, треугольные числа и геометрия тесно связаны друг с другом. Использование треугольных чисел в математике и геометрии может помочь в решении различных задач и нахождении закономерностей в числовых рядах.

Примеры использования треугольных чисел в математике

1. Сумма натуральных чисел

Первый пример использования треугольных чисел в математике — это нахождение суммы натуральных чисел. Замечательно, что сумма первых n натуральных чисел может быть выражена формулой n(n+1)/2. Таким образом, треугольные числа можно использовать для быстрого нахождения суммы больших последовательностей чисел, что может быть полезно в различных задачах и алгоритмах.

2. Комбинаторика

Треугольные числа также используются в комбинаторике для подсчета количества способов выбрать определенное количество элементов из заданного множества. Например, количество способов выбрать k элементов из множества из n элементов может быть вычислено с помощью треугольных чисел. Формула для этого выражения: C(n, k) = n! / (k!(n-k)!), где C(n, k) — это число сочетаний.

3. Геометрия

В геометрии треугольные числа могут использоваться для нахождения общего количества точек, линий и треугольников в фигуре. Например, для нахождения общего количества точек в треугольнике, можно использовать формулу треугольных чисел и добавить количество вершин и серединных точек на каждой стороне треугольника. Также треугольные числа могут использоваться для вычисления общего количества прямоугольников, которые можно составить из заданного количества точек.

4. Работа с рядами

Треугольные числа также используются при работе с рядами чисел. Например, в числовой последовательности «1, 3, 6, 10, 15, …» каждое число является треугольным числом, а также представляет собой сумму натуральных чисел. Это связано с тем, что каждый элемент ряда получается путем прибавления к предыдущему номера следующего элемента.

Треугольные числа широко используются в различных областях математики, физики, программирования и других науках. Их свойства и формулы сыграли важную роль в развитии математической теории и находят практическое применение в решении различных задач.

Треугольные числа и комбинаторика

Треугольные числа находят широкое применение в комбинаторике. Комбинаторика — это раздел математики, изучающий различные комбинации и перестановки объектов. Треугольные числа помогают в решении задач, связанных с перестановками и комбинациями.

Одно из основных свойств треугольных чисел — их связь с биномиальными коэффициентами. Биномиальные коэффициенты используются для вычисления количества комбинаций, которые можно сформировать из заданного множества объектов. Они также используются в различных областях, таких как теория вероятности, статистика и алгебра.

Треугольные числа можно представить в виде таблицы, где каждое число является суммой двух чисел, расположенных выше него. Такая таблица называется треугольником Паскаля и широко используется в комбинаторике и алгебре. В треугольнике Паскаля каждое число представляет собой биномиальный коэффициент и имеет связь с треугольными числами.

Треугольные числа также используются для решения задач, связанных с суммами числовых рядов, комбинаторными перестановками и делением объектов на группы. Они играют важную роль в различных областях математики и имеют множество приложений в реальном мире.

Треугольные числа в криптографии

Треугольные числа также находят свое применение в области криптографии. Это связано с их особенностями и возможностью использования их в качестве ключей для шифрования данных.

Одним из способов использования треугольных чисел в криптографии является их применение в качестве части алгоритма генерации псевдослучайных чисел. Псевдослучайные числа, полученные на основе треугольных чисел, обладают высокой степенью непредсказуемости и могут использоваться для создания шифров и ключей, которые сложно взломать.

Также треугольные числа могут быть использованы в качестве индексов для доступа к элементам в таблицах секретных ключей. Поскольку треугольные числа имеют определенный порядок и уникальность, они могут служить в качестве уникальных идентификаторов для определенных ключей или значений, которые используются в криптографических алгоритмах.

Треугольные числа также могут быть использованы для вычисления контрольных сумм в криптографических алгоритмах. Контрольная сумма представляет собой число, которое вычисляется на основе данных, и используется для проверки целостности и подлинности информации. Использование треугольных чисел для вычисления контрольных сумм может повысить уровень безопасности данных и сделать алгоритмы криптографии более устойчивыми к взлому.

Таким образом, треугольные числа играют важную роль в криптографии и находят применение в различных аспектах этой науки. Их специфические свойства и уникальность делают их ценными инструментами для создания безопасных шифров и ключей для защиты информации.

Связь треугольных чисел с числами Фибоначчи

Треугольные числа и числа Фибоначчи имеют интересную связь. Числа Фибоначчи образуются путем сложения двух предыдущих чисел, начиная с 0 и 1. Таким образом, последовательность чисел Фибоначчи выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, и так далее.

С другой стороны, треугольные числа можно представить в виде треугольной формы, где каждое число представляет сумму всех чисел от 1 до данного числа. Например, первое треугольное число равно 1 (1), второе — 3 (1+2), третье — 6 (1+2+3), четвертое — 10 (1+2+3+4), и так далее.

Интересно, что сумма первых n треугольных чисел равна числу Фибоначчи с номером n+2. Например, сумма первых 3 треугольных чисел равна 10, а третье число Фибоначчи также равно 10. Аналогично, сумма первых 4 треугольных чисел равна 20, а четвертое число Фибоначчи также равно 20.

Эта связь между треугольными числами и числами Фибоначчи может быть полезной в различных математических исследованиях и приложениях. Она позволяет переходить от одного вида чисел к другому и находить интересные закономерности и свойства в обоих последовательностях чисел.

Треугольные числаЧисла Фибоначчи

1	0
3	1
6	1
10	2
15	3
21	5
28	8
36	13

Таким образом, числа Фибоначчи и треугольные числа тесно связаны и могут использоваться для решения различных задач в математике.

Вопрос-ответ:

Что такое треугольные числа?

Треугольные числа — это числа, которые могут быть представлены в виде треугольной формы, где каждый следующий ряд чисел имеет на одно число больше, чем предыдущий ряд. Например, 1, 3, 6, 10 и так далее.

Как вычислить треугольное число?

Для вычисления треугольного числа можно использовать формулу n * (n + 1) / 2, где n — номер треугольного числа. Например, для вычисления 5-го треугольного числа, нужно подставить 5 в формулу: 5 * (5 + 1) / 2 = 15.

Где используются треугольные числа в математике?

Треугольные числа используются в различных областях математики. Например, они используются для решения задач комбинаторики, в теории вероятности, в теории чисел. Также треугольные числа применяются в геометрии и в алгоритмах.

Можно ли найти треугольные числа в природе?

Нет, треугольные числа — это абстрактные математические объекты. Они не имеют прямого отношения к природе и не могут быть найдены в естественном мире. Однако, треугольные формы встречаются в некоторых геометрических объектах, например, в пирамидах или треугольной решетке.