Что значит убывание в математике

Убывание в математике означает, что функция или последовательность уменьшается по мере увеличения аргумента или индекса. Убывающая функция имеет отрицательный наклон, а убывающая последовательность имеет все меньшие элементы. Убывание в математике является важным понятием, которое помогает анализировать поведение функций и последовательностей.

В математике убывание является одним из ключевых понятий, которое используется для описания изменения значений функции или последовательности. Убывание означает, что значения функции или последовательности уменьшаются при увеличении аргумента или номера элемента соответственно. Наличие убывания может быть важным фактором при решении различных задач и применении математических моделей.

Для того чтобы определить, убывает ли функция или последовательность, необходимо проанализировать изменение их значений. Если при увеличении аргумента или номера элемента значения уменьшаются, то говорят, что функция или последовательность убывают. Это означает, что с ростом аргумента или номера элемента, значение функции или последовательности уменьшается.

Убывание имеет широкое применение в различных областях, в том числе в экономике, физике, биологии и многих других. Например, в экономике убывание может описывать снижение спроса на товары при увеличении их цены. В физике убывание может характеризовать затухание амплитуды колебаний. В биологии убывание может описывать уменьшение численности популяции при увеличении конкуренции за ресурсы.

Использование понятия убывания позволяет более точно описывать и анализировать различные явления и процессы в науке и реальном мире. Оно помогает выявить закономерности и предсказать возможные изменения в зависимости от изменения аргумента или номера элемента.

В заключение, убывание в математике представляет собой важное понятие, которое позволяет описать и анализировать изменение значений функций и последовательностей. Оно имеет широкое применение в различных областях и помогает выявить закономерности и предсказать возможные изменения в зависимости от изменения аргумента или номера элемента.

Убывание функции

Для определения убывания функции необходимо анализировать знак производной функции. Если производная функции отрицательна на заданном интервале, то функция является убывающей на этом интервале.

Убывание функции имеет важные приложения в различных областях математики и естественных наук. Например, в физике убывание функции может описывать уменьшение скорости тела при движении или уменьшение концентрации вещества в химической реакции. В экономике убывание функции может моделировать уменьшение спроса при увеличении цены товара.

Понимание убывания функции важно для решения различных задач и оптимизации процессов. Анализ убывания функции позволяет определить, как изменение аргумента влияет на значение функции и принять рациональные решения.

Видео по теме:

Понятие убывания в математике

При убывании функции, значения находятся на «нижней» стороне графика функции. Также можно сказать, что убывание означает, что функция имеет отрицательный наклон. Например, функция f(x) = -2x является убывающей, так как значения уменьшаются с ростом значения аргумента x.

В случае числовых последовательностей, убывание подразумевает, что каждый следующий элемент последовательности меньше предыдущего. Например, последовательность 1, 0.9, 0.8, 0.7, … является убывающей, так как каждый следующий элемент меньше предыдущего.

Понятие убывания имеет важное значение в различных областях математики, таких как анализ функций, дифференциальное исчисление, теория вероятностей и других. Оно помогает описывать и анализировать изменение величин и отношения между ними.

Как распознать убывание функции

1. Анализ производной. Если производная функции отрицательна на интервале, то функция убывает на этом интервале. Для этого нужно вычислить производную функции и проанализировать ее знак на интервале.
2. Исследование монотонности. Если функция монотонно убывает на интервале, то она убывает на всем этом интервале. Для этого нужно вычислить производную функции, найти ее экстремумы и исследовать знаки производной между экстремумами.
3. Графический метод. Если график функции убывает на всем промежутке, то функция убывает на этом промежутке. Для этого нужно построить график функции и проанализировать его наклон.

Каждый из этих методов имеет свои особенности и может быть применен в зависимости от конкретной задачи. Важно уметь правильно применять эти методы для определения убывания функции и использовать их в соответствующих ситуациях.

Вопрос-ответ:

Что такое убывание в математике?

Убывание — это свойство функции или последовательности, при котором ее значения уменьшаются по мере увеличения аргумента.

Как можно определить убывание функции?

Функция считается убывающей на определенном интервале, если для любых двух точек из этого интервала, значение функции в первой точке будет меньше значения функции во второй точке.

Как применяется убывание в математике?

Убывание может быть полезным свойством функции в решении различных задач. Например, оно может использоваться для нахождения максимальных и минимальных значений функции, а также для определения моментов, когда функция достигает определенного значения.

Какая разница между убыванием и возрастанием функции?

Убывание и возрастание — это противоположные свойства функций. Убывание означает, что значения функции уменьшаются при увеличении аргумента, а возрастание — что значения функции увеличиваются при увеличении аргумента.

Есть ли специальные обозначения для убывания функции?

Да, для обозначения убывания функции можно использовать специальное обозначение — стрелку вниз ↑.

Почему убывание важно

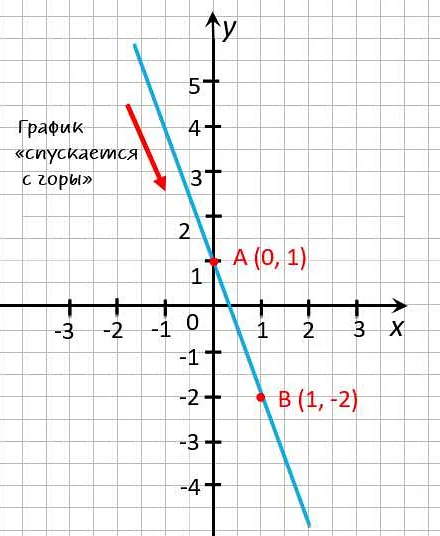
Убывание позволяет нам анализировать изменение величин, учитывать их тенденции и прогнозировать будущие значения. Например, при изучении экономических данных, знание убывания позволяет определить, как меняется спрос на товары или услуги и какие факторы влияют на этот спрос.

Убывание также играет важную роль в физике, где позволяет анализировать изменение физических величин с течением времени. Это помогает предсказывать, например, скорость движения тела или изменение температуры в определенном процессе.

Знание убывания также полезно при решении задач на оптимизацию. Например, при минимизации затрат или максимизации прибыли компании нужно учитывать убывание различных факторов, чтобы принять оптимальное решение.

Важно также отметить, что знание убывания помогает нам понимать и анализировать графики и функции. Умение определять убывание функции позволяет понять, как меняется ее значение при изменении аргумента и какие возможны экстремальные точки или точки перегиба.

В целом, убывание является фундаментальным понятием в математике и имеет множество применений в различных областях. Понимание убывания помогает нам анализировать данные, прогнозировать значения и принимать оптимальные решения.

Применение убывания в математике

Одно из основных применений убывания в математике — это нахождение максимальных и минимальных значений функций. Если функция убывает на заданном интервале, то ее максимальное значение достигается на его конце, а минимальное значение — на его начале. Это позволяет определить точки экстремума функции и использовать их для решения различных задач.

Убывание также используется при анализе графиков функций. Если график функции имеет участок, на котором он строго убывает, это может указывать на наличие определенных закономерностей или зависимостей между переменными. Также убывание может помочь определить области, в которых функция уменьшается или увеличивается, что может быть полезно при решении прикладных задач.

Одним из примеров применения убывания является анализ экономических данных. Если, например, спрос на товар убывает с увеличением его цены, это может указывать на обратную зависимость между спросом и ценой и помочь в принятии решений по управлению предложением и спросом.

Графическое представление убывания

Для построения графика убывающей функции необходимо знать точки, в которых функция убывает. На графике убывающей функции значения функции на оси ординат будут уменьшаться по направлению сверху вниз. График убывающей функции может иметь различную форму, например, может быть линейным, параболическим или экспоненциальным.

График убывающей функции часто используется для анализа данных и прогнозирования. Например, если мы имеем график убывающей функции, то можем сделать вывод о том, что значения функции будут уменьшаться и дальше. Это позволяет делать прогнозы и принимать решения на основе имеющихся данных.

Построение графика убывающей функции может быть полезным инструментом для визуализации и анализа данных. Оно позволяет наглядно представить изменение значений функции и легче понять их свойства. Графическое представление убывания позволяет увидеть тренды и закономерности, что может быть полезно для принятия решений и планирования дальнейших действий.

Пример графика убывающей функции

^ | | / | / | / | / +———————> x

Математические примеры убывания

В математике убывание означает уменьшение или уход от нуля. Ниже приведены несколько примеров математического убывания.

Пример 1:

Рассмотрим последовательность чисел: 10, 8, 6, 4, 2. В данном примере каждое следующее число меньше предыдущего на 2. Таким образом, эта последовательность убывает.

Пример 2:

Пусть имеется функция y = x^2, где x — переменная. Если значение x увеличивается, то значение y убывает. Например, при x = 3, y = 9, а при x = 4, y = 16. Значение y увеличивается медленнее, чем значение x, поэтому функция y = x^2 является убывающей.

Пример 3:

Рассмотрим геометрическую прогрессию с первым членом a = 100 и знаменателем q = 0.5. Члены прогрессии будут следующими: 100, 50, 25, 12.5. Каждый следующий член прогрессии меньше предыдущего вдвое. Таким образом, геометрическая прогрессия убывает.

Математические примеры убывания демонстрируют, как значения или члены последовательности уменьшаются или уходят от нуля. Понимание убывания в математике важно для анализа и решения различных задач.