Что такое равенство математика
Содержимое
- 1 Что такое равенство математика
- 1.1 Основные понятия равенства в математике
- 1.2 Видео по теме:
- 1.3 Что такое равенство в математике?
- 1.4 Коммутативность равенства
- 1.5 Вопрос-ответ:
- 1.6 Транзитивность равенства
- 1.7 Рефлексивность равенства
- 1.8 Свойства равенства
- 1.9 Примеры равенства
- 1.10 Применение равенства в уравнениях
- 1.11 Знаки равенства и неравенства
Равенство в математике представляет собой отношение между двумя выражениями или числами, которые имеют одинаковое значение. Узнайте, как определить, доказать и использовать равенство в математике, а также о различных типах равенств и ее свойствах.
Равенство — одно из основных понятий в математике, являющееся основой для решения различных задач и построения математических моделей. В математических выражениях равенство используется для указания равенства двух выражений или объектов. Понимание равенства является ключевым для понимания многих других математических концепций.
Основное правило равенства гласит, что два выражения или объекта равны, если они представляют одно и то же значение. В математике равенство обозначается символом «=» и часто используется в уравнениях. Например, уравнение «2 + 2 = 4» показывает, что сумма двух чисел 2 равна числу 4.
Равенство имеет несколько свойств, которые помогают в работе с математическими выражениями. Одно из таких свойств — свойство симметричности равенства. Оно гласит, что если два выражения равны, то можно поменять их местами без изменения равенства. Например, если «a = b», то также верно «b = a».
Одной из основных задач равенства в математике является нахождение неизвестных значений. Для этого часто используется алгебраическое решение уравнений. Например, в уравнении «3x + 4 = 10» мы ищем значение переменной «x», при котором оба выражения будут равными.
В математике также существуют различные типы равенств, такие как тождественное равенство, условное равенство и асимптотическое равенство. Каждый из них имеет свои особенности и применяется в различных областях математики и наук.
Основные понятия равенства в математике

Основные символы, используемые для обозначения равенства, — это знак «=» (равно) и знаки «≠» (не равно). Знак «=» используется для утверждения, что два выражения или значения равны, тогда как знак «≠» используется для утверждения, что они не равны.
Равенство в математике имеет следующие основные свойства:
СвойствоОписаниеПример
| Рефлексивность | Любое значение равно самому себе | a = a |
| Симметричность | Если a равно b, то b равно a | a = b → b = a |
| Транзитивность | Если a равно b и b равно c, то a равно c | a = b и b = c → a = c |
| Замена равных на равные | Если a равно b, то можно заменить a на b и наоборот | Если a = b, то a + c = b + c |
В математике равенство может быть использовано для решения уравнений, проведения математических доказательств и установления соотношений между различными величинами.
Понимание основных понятий равенства в математике является важным для успешного изучения более сложных математических концепций и применения их на практике.
Видео по теме:
Что такое равенство в математике?
Равенство обозначается знаком «=» и может использоваться для сравнения чисел, переменных, функций, уравнений и других математических объектов.
В математике равенство может быть использовано для:
- Сравнения чисел: например, 2 + 2 = 4.
- Определения переменных: например, x = 5.
- Сравнения функций: например, f(x) = g(x).
- Решения уравнений: например, x^2 — 4 = 0.
Важно отличать равенство от других математических отношений, таких как неравенство или эквивалентность. Равенство говорит о полном совпадении двух объектов, в то время как неравенство указывает на различие в их значениях. Эквивалентность означает, что два объекта имеют одинаковое математическое значение или свойство, но могут отличаться по другим аспектам.
Равенство в математике играет ключевую роль во всех ее областях, и является одним из основных понятий, которые используются для построения математических моделей и доказательств.
Коммутативность равенства
Например, для любых чисел a и b, a + b = b + a. Это означает, что сумма двух чисел не зависит от порядка их слагаемых.
Коммутативность равенства широко используется в математике для упрощения записи и вычислений. Когда мы меняем порядок элементов в равенстве, мы можем сократить его запись и упростить дальнейшие рассуждения.
В таблице ниже приведены примеры коммутативности равенства для различных операций:
ОперацияПример коммутативности равенства
| Сложение | a + b = b + a |
| Умножение | a * b = b * a |
| Логическое И | a && b = b && a |
| Логическое ИЛИ | a || b = b || a |
Нужно отметить, что не все операции обладают свойством коммутативности равенства. Например, для вычитания и деления это свойство не выполняется.
Важно помнить, что коммутативность равенства применима только для операций, для которых она доказана. При использовании других операций следует проверить, обладают ли они свойством коммутативности равенства.
Вопрос-ответ:
Какое определение равенства в математике?
В математике равенство — это отношение между двумя математическими объектами, которые считаются одинаковыми или эквивалентными. Если два объекта равны, то они обладают одинаковыми свойствами и характеристиками.
Какие основные понятия связаны с равенством в математике?
Основные понятия, связанные с равенством в математике, включают: равные числа, равные уравнения, равные многочлены и равные геометрические фигуры. Все эти понятия описывают ситуации, в которых два или более объекта имеют одинаковое значение, форму или свойства.
Какие примеры равенства можно привести?
Примеры равенства в математике включают: 2 + 2 = 4, x + 3 = 7 (где x = 4), (x + y)^2 = x^2 + 2xy + y^2, и прямоугольник с шириной 5 и длиной 5, который имеет ту же площадь, что и квадрат со стороной 5.
Какими свойствами должны обладать объекты, чтобы быть равными?
Чтобы два объекта считались равными, они должны иметь одинаковое значение, форму или свойства. Например, два числа считаются равными, если их числовые значения одинаковы. Для равных геометрических фигур, их формы и размеры должны быть одинаковыми. В равных уравнениях, их решения должны быть одинаковыми.
Какое значение равенства в математике для решения проблем?
Равенство в математике играет важную роль в решении проблем и задач. Оно позволяет устанавливать соответствия между различными объектами и применять различные методы математики, такие как алгебра и геометрия, для решения проблем. Равенство также позволяет устанавливать и проверять логические связи и выводы в математических доказательствах.
Транзитивность равенства
Транзитивное свойство равенства утверждает, что если два выражения равны друг другу, и второе выражение равно третьему, то первое выражение также будет равно третьему выражению.
Другими словами, если у нас есть равенства A = B и B = C, то мы можем заключить, что A = C. Это означает, что равенство транзитивно и позволяет нам строить цепочки равенств.
Например, пусть у нас есть равенства x + 2 = 7 и 7 = 3y. С использованием транзитивности равенства, мы можем заключить, что x + 2 = 3y. Таким образом, через цепочку равенств мы можем связать значение x и y.
Транзитивность равенства является важным инструментом в математике, который позволяет нам проводить логические рассуждения и делать выводы на основе уже известных равенств.
Примечание: транзитивность равенства также действует и в обратную сторону. То есть, если у нас есть равенство A = C и A = B, то мы можем заключить, что B = C.
Рефлексивность равенства
Формально можно записать, что для любого объекта a, a = a. Это означает, что любое значение или выражение равно самому себе.
Например, если a = 5, то 5 = 5. Это является примером простой рефлексивности равенства.
Рефлексивность равенства является основным свойством, используемым во многих математических доказательствах и рассуждениях. Она позволяет устанавливать равенство между объектами и использовать его в дальнейших рассуждениях.
Свойства равенства

В математике имеется несколько свойств равенства, которые позволяют делать различные преобразования и упрощения выражений:
- Симметричность: если a = b, то b = a. Это свойство позволяет менять местами выражения в равенстве. Например, если 2 + 3 = 5, то также можно сказать, что 5 = 2 + 3.
- Транзитивность: если a = b и b = c, то a = c. Это свойство позволяет объединять несколько равенств в одно. Например, если 2 + 3 = 5 и 5 = 7 — 2, то можно сказать, что 2 + 3 = 7 — 2.
- Рефлексивность: любое выражение равно самому себе. Например, 2 + 3 = 2 + 3.
- Замена: если a = b, то a можно заменить на b и наоборот. Например, если 2 + 3 = 5, то можно заменить выражение «2 + 3» на «5» и наоборот.
- Тождество: можно добавить или вычесть одно и то же число с обеих сторон равенства. Например, если a = b, то a + c = b + c и a — c = b — c.
- Умножение и деление: можно умножить или разделить обе стороны равенства на одно и то же число, отличное от нуля. Например, если a = b и c ≠ 0, то a * c = b * c и a / c = b / c.
Свойства равенства позволяют проводить различные преобразования выражений, сохраняя их равенство. Это является основой для решения уравнений и работы с различными математическими объектами.
Примеры равенства
Примеры равенства:
1. 2 + 2 = 4 — это пример равенства между двумя выражениями, которые имеют одно и то же значение.
2. x + 5 = 10 — это пример равенства, где значение неизвестной переменной x можно найти путем решения уравнения.
3. 5 / 2 = 2.5 — это пример равенства между десятичной дробью и обыкновенной дробью.
4. a^2 + b^2 = c^2 — это пример равенства в геометрии, известный как теорема Пифагора.
5. cos^2(x) + sin^2(x) = 1 — это пример равенства в тригонометрии, известный как тождество тригонометрии.
Равенство играет важную роль в математике, так как позволяет устанавливать связь между различными выражениями и решать уравнения для нахождения значений переменных.
Применение равенства в уравнениях
В уравнении равенство используется для выражения равенства значений двух математических выражений или функций. Левая часть уравнения обозначает то, что нужно сравнить или вычислить, а правая часть – то, с чем нужно это сравнить.
Применение равенства в уравнениях позволяет находить неизвестные значения и решать различные математические задачи. Уравнения используются в различных областях математики, физики, химии, экономике и других науках.
Например, рассмотрим следующее уравнение:
2x + 5 = 13
В этом уравнении знак равенства (=) указывает на то, что левая часть выражения 2x + 5 равна правой части выражения 13. Для решения уравнения нужно найти значение переменной x, которое удовлетворяет равенству.
Для решения этого уравнения можно выполнить следующие шаги:
- Вычесть 5 из обеих частей уравнения: 2x + 5 — 5 = 13 — 5
- Упростить: 2x = 8
- Разделить обе части уравнения на 2: (2x) / 2 = 8 / 2
- Упростить: x = 4
Таким образом, решением уравнения 2x + 5 = 13 является x = 4.
Применение равенства в уравнениях позволяет находить решения для различных неизвестных величин и используется для моделирования и анализа различных явлений в математике и других науках.
Знаки равенства и неравенства

В математике для обозначения равенства используется специальный знак «=», который читается как «равно». Знак равенства указывает на то, что две математические выражения или числа равны друг другу.
Например, если у нас есть выражение 2 + 2 = 4, то это означает, что сумма двух чисел «2» равна числу «4».
Кроме знака равенства, в математике также используется знак неравенства «<>». Знак неравенства указывает на то, что два математические выражения или числа не равны друг другу.
Например, если у нас есть выражение 3 + 2 <> 6, то это означает, что сумма трех и двух равна числу «6».
Кроме знака неравенства, существуют также другие знаки сравнения, такие как «» (больше), «=» (больше или равно). Они используются для обозначения отношений между числами или выражениями.
Например, выражение 5 < 10 означает, что число «5» меньше числа «10».
Знаки равенства и неравенства играют важную роль в математике при решении уравнений, неравенств и других задач.
ЗнакОписаниеПример
| = | равно | 2 + 2 = 4 |
| <> | не равно | 3 + 2 <> 6 |
| < | меньше | 5 < 10 |
| > | больше | 10 > 5 |
| ≤ | меньше или равно | 5 ≤ 10 |
| ≥ | больше или равно | 10 ≥ 5 |

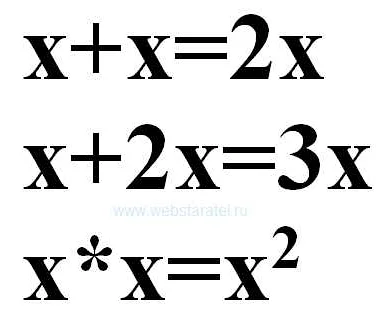



Отличная статья! Большое спасибо за ясное и понятное объяснение понятия равенства в математике. Часто слышу это слово, но до конца не понимал его смысл. Теперь все стало ясно! Равенство — это когда два числа или выражения равны друг другу. Например, 2+2=4 или x^2=25. Важно знать, что равенство всегда требует, чтобы обе части были абсолютно идентичными. Равенство используется в различных областях математики и является основным понятием для решения уравнений и задач. Это просто потрясающе, как математика помогает нам понять и описывать мир вокруг нас. Спасибо за познавательную статью! Жду с нетерпением новые материалы на эту тему.
Статья очень понятно и доступно объясняет, что такое равенство в математике. Я всегда задавался вопросом, как определить, что два выражения равны друг другу, и наконец-то получил ответ. Очень интересно было узнать, что равенство — это отношение, при котором два выражения имеют одинаковое значение. Приведенные примеры с цифрами и переменными помогли мне лучше понять это понятие. Теперь я знаю, что равенство — это не только знак «=» между числами, но и между алгебраическими выражениями. Статья ясно объясняет основные правила равенства и показывает, каким образом можно упростить или преобразовать выражения с помощью равенств. Я благодарен автору за столь подробное объяснение и примеры, которые помогли мне лучше усвоить это понятие. Теперь я чувствую себя увереннее в своих знаниях о равенстве в математике.
Статья о равенстве в математике отлично раскрывает основные понятия и примеры данной математической операции. Я, как читатель, благодарна автору за доступное изложение сложной темы. Равенство — это не только знак равенства, но и математическое утверждение о равенстве двух выражений. Примеры сравнений чисел и алгебраических выражений позволяют наглядно представить, как применять равенство в практических задачах. Статья помогла мне лучше понять суть равенства и его важность в математике. Рекомендую всем, кто хочет углубить свои знания в этой области, ознакомиться с данной статьей.