Что такое вершины в математике 4 класс

Вершины – это точки, в которых пересекаются ребра геометрических фигур. В математике для 4 класса вершины используются для определения формы фигуры и решения задач по геометрии.

Вершины — одно из основных понятий, которое дети изучают в четвертом классе по программе математики. Вершины – это точки пересечения ребер в геометрических фигурах, таких как треугольники, прямоугольники и многоугольники. Понимание понятия вершины очень важно для развития логического мышления и геометрической интуиции у детей.

Вершины можно представить как углы в фигуре. Например, в треугольнике есть три вершины, каждая из которых является точкой пересечения двух его сторон. В прямоугольнике есть четыре вершины, каждая из которых является точкой пересечения двух его сторон. В многоугольнике количество вершин зависит от количества его сторон и может быть любым.

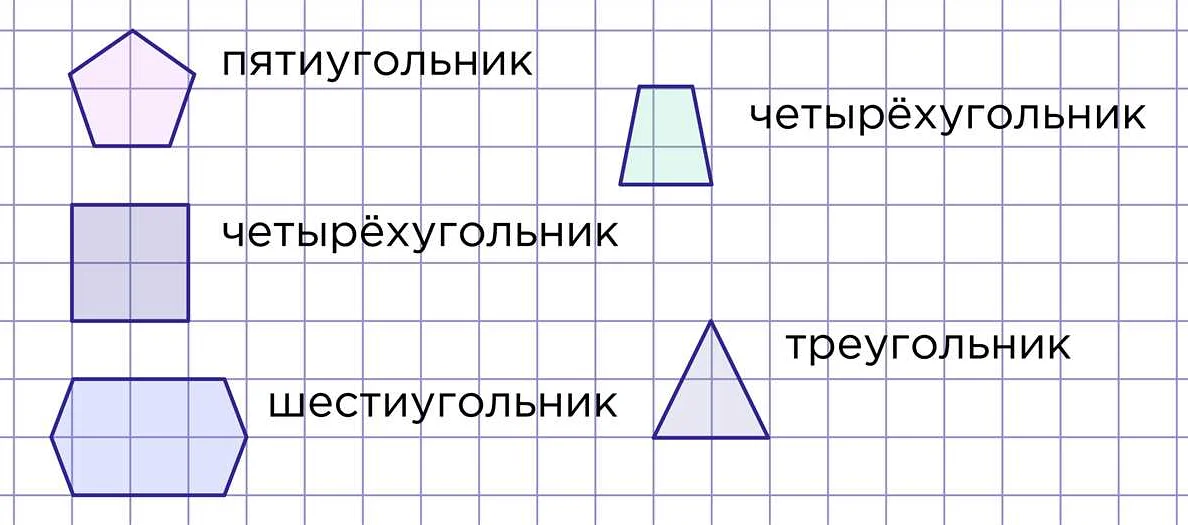
Примеры геометрических фигур с вершинами:

— Треугольник: 3 вершины

— Прямоугольник: 4 вершины

— Пятиугольник: 5 вершин

— Шестиугольник: 6 вершин

— Многоугольник: любое количество вершин

Знание понятия вершины позволяет детям обозначать и считать количество вершин в различных фигурах, а также рассматривать их свойства и характеристики. Это основа для дальнейшего изучения геометрии и решения задач на построение и сравнение фигур.

Вершины в математике 4 класс

Для лучшего понимания понятия «вершины» давайте рассмотрим несколько примеров.

Геометрическая фигураПримеры вершин

Треугольник	Вершины треугольника – это точки, где пересекаются его стороны. Например, треугольник ABC имеет вершины A, B и C.
Квадрат	У квадрата также есть вершины – это точки, где пересекаются его стороны. Например, квадрат DEF имеет вершины D, E, F и G.
Прямоугольник	Вершины прямоугольника – это точки, где пересекаются его стороны. Например, прямоугольник HIJK имеет вершины H, I, J и K.

Таким образом, понятие вершин играет важную роль в геометрии и помогает определить особенности геометрических фигур.

Понятие вершины и ее характеристики

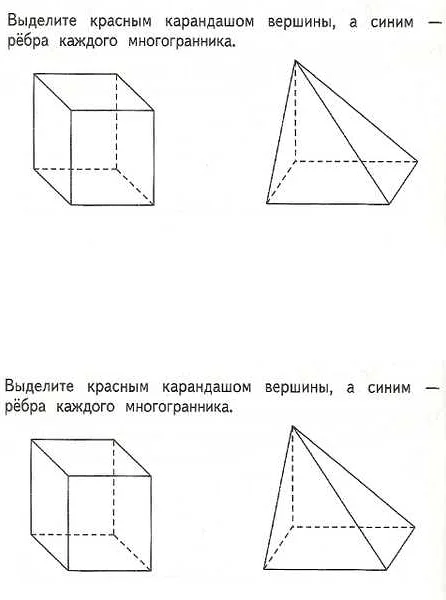
Характеристики вершин могут варьироваться в зависимости от контекста. В геометрии вершина может иметь определенные координаты (x, y), которые задают ее положение на плоскости. Кроме того, у вершины могут быть определены дополнительные характеристики, такие как углы, длины сторон и радиусы окружностей.

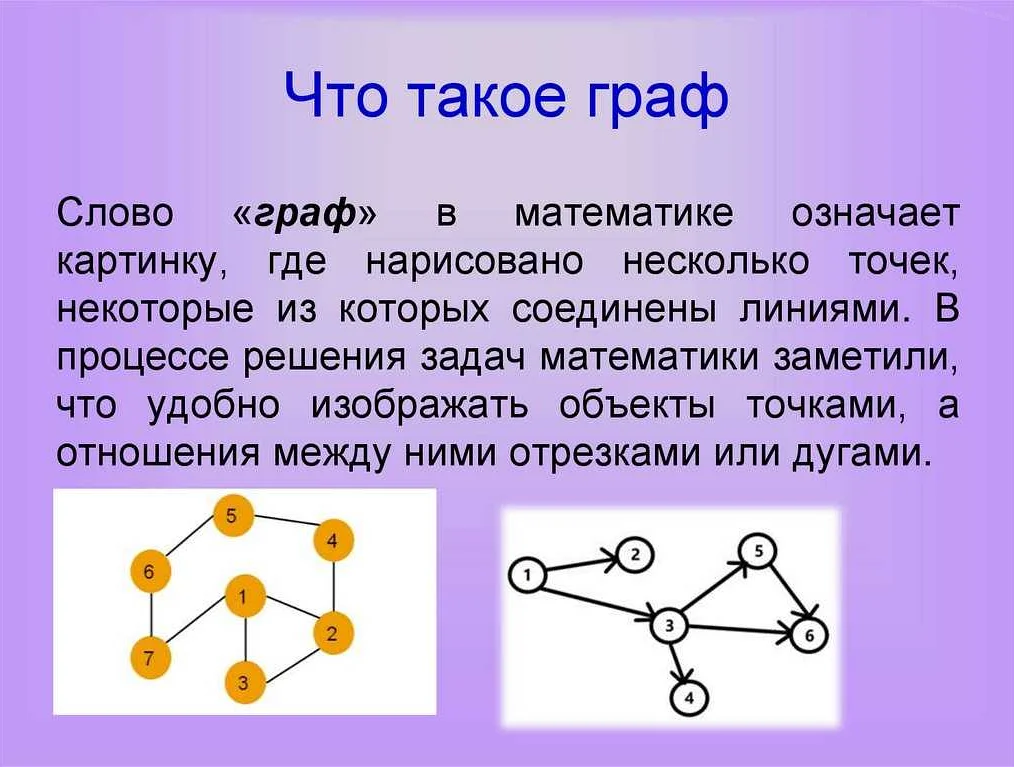
В теории графов вершина является основной строительной единицей. Вершины могут быть пронумерованы или обозначены буквами. Они могут быть связаны друг с другом ребрами, которые представляют собой связи или отношения между вершинами. Каждая вершина может иметь определенные свойства или атрибуты, которые могут быть использованы для анализа графа.

Вершины могут иметь разные степени, которые определяются количеством ребер, связанных с данной вершиной. Вершина с нулевой степенью называется изолированной, а вершина с максимальной степенью называется центральной или главной вершиной.

ПримерОписание

A	Вершина с идентификатором «A»
B	Вершина с идентификатором «B»
C	Вершина с идентификатором «C»

Вершины могут быть использованы для моделирования различных ситуаций, например, в географических картах, схемах сетей, деревьях и т.д. Изучение вершин позволяет анализировать и понимать взаимосвязи и взаимодействия между различными элементами в этих моделях.

Графическое представление вершины

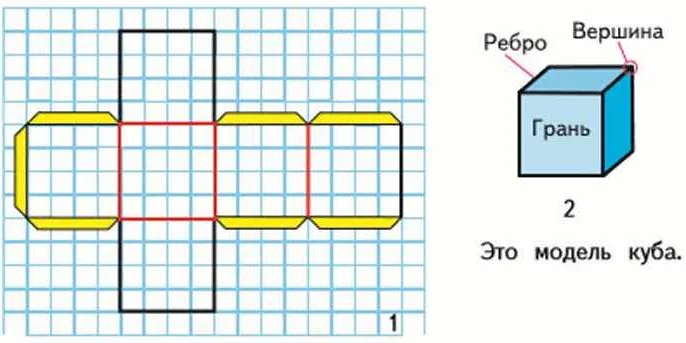
В математике вершина представляет собой точку, которая может быть обозначена на графическом изображении. Графическое представление вершины может быть в виде кружка или точки, которая обозначает собой местоположение вершины на плоскости.

Кружок или точка, обозначающая вершину, часто имеет маленький диаметр или размер, чтобы не перекрывать другие элементы на графическом изображении. Однако, они должны быть достаточно отчетливыми, чтобы их можно было легко увидеть и распознать на графическом представлении.

Часто вершины в графическом представлении связываются линиями или отрезками, которые указывают на связи между вершинами. Такие линии могут быть прямыми или пунктирными, чтобы указать различные типы связей.

Графическое представление вершины является важным инструментом для визуализации и анализа графов. Оно позволяет увидеть структуру графа, взаимосвязи между вершинами и легко определить основные элементы графа.

Использование графического представления вершин помогает в понимании и анализе математических концепций, связанных с графами, и способствует развитию визуального мышления у учащихся.

Вершины в геометрии

Вершинами в геометрии называются точки, в которых сходятся две или более прямых линии или отрезки. Вершины могут быть найдены в различных геометрических фигурах, таких как треугольники, квадраты, прямоугольники и т.д.

В треугольнике, вершинами являются три точки, соответствующие концам трех его сторон. В квадрате и прямоугольнике, вершинами являются четыре угла фигуры.

Вершины играют важную роль в геометрии, так как они определяют форму и размеры фигур. Они также помогают в определении свойств и характеристик фигур. Например, в треугольнике, вершины определяют его тип (равносторонний, равнобедренный или разносторонний).

Для определения вершин в геометрической фигуре необходимо провести соответствующие линии и найти точки их пересечения. Вершины обозначаются заглавными буквами, такими как A, B, C и т.д.

Знание понятия вершины в геометрии поможет вам в анализе и решении различных геометрических задач. При решении задач не забывайте обращать внимание на вершины фигур и использовать их свойства и характеристики.

Вершины в арифметике

Вершины помогают нам определить максимальное или минимальное значение из группы чисел. Чаще всего вершины используются при решении задач на нахождение экстремальных значений функций.

Для нахождения вершины графика функции, необходимо найти точку, в которой функция достигает своего максимального или минимального значения. Вершина может быть точкой максимума или точкой минимума.

Например, при решении уравнения y = x^2, вершина графика функции будет находиться в точке (0,0). В данном случае, функция достигает своего минимального значения в точке (0,0).

Также, вершины могут быть использованы для определения экстремальных значений в задачах на нахождение максимального или минимального значения.

Например, при решении задачи на нахождение максимальной площади прямоугольника с заданным периметром, вершина заданной области будет точкой, в которой площадь прямоугольника будет максимальной.

Вершины играют важную роль в арифметике, позволяя нам определить максимальное или минимальное значение из группы чисел. Их использование позволяет нам решать различные задачи и находить экстремальные значения функций.

Примеры вершин

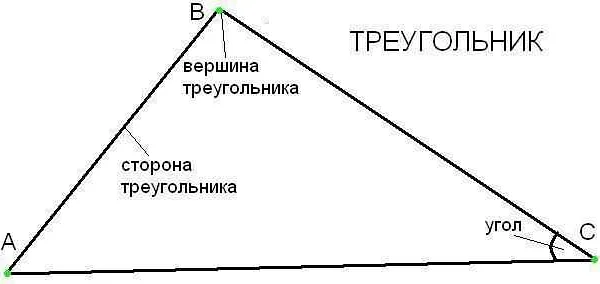
Пример 1: Рассмотрим треугольник ABC. Вершины данного треугольника обозначаются буквами A, B и C. Точка A — это вершина угла ABC, точка B — это вершина угла BAC, а точка C — это вершина угла ACB.

Пример 2: Пусть у нас есть прямоугольник PQRS. Точка P — это одна из вершин прямоугольника, точка Q — это вершина, расположенная напротив точки P, точка R — это вершина противоположная точке Q, а точка S — это вершина противоположная точке P.

Пример 3: Изображенный на рисунке многоугольник имеет 6 вершин. Они обозначаются буквами A, B, C, D, E и F. Каждая из этих точек является вершиной угла многоугольника.

Таким образом, вершины представляют собой точки, образующие углы в геометрии. Приведенные примеры демонстрируют, как вершины обозначаются и как они могут быть использованы для определения углов и формы фигур.

Видео по теме:

Вопрос-ответ:

Что такое вершина в математике?

Вершина в математике — это точка, в которой сходятся два или более отрезка, луча или прямой. Вершины могут быть использованы для определения геометрических фигур, таких как треугольники, квадраты и многоугольники.

Какие примеры вершин можно найти в окружающем нас мире?

Примеры вершин можно найти во многих объектах окружающей среды. Например, углы стола, углы окна, углы книжной полки — все это примеры вершин. Также вершинами могут быть крыши домов, углы зданий и многое другое.

Какие свойства имеют вершины?

Вершины имеют несколько свойств. Во-первых, они являются точками схода отрезков, лучей или прямых. Во-вторых, они определяют углы, которые могут быть различной величины, в зависимости от расположения отрезков. В-третьих, вершины могут быть использованы для определения геометрических фигур.

Как можно использовать понятие вершин в повседневной жизни?

Понятие вершин можно использовать в повседневной жизни для определения геометрических фигур, а также для решения задач, связанных с измерением углов и расположением объектов в пространстве. Например, при проектировании мебели или при ремонте дома можно использовать знание о вершинах для создания правильных углов и геометрических пропорций.

Каким образом вершины могут быть использованы в математических задачах?

Вершины могут быть использованы в математических задачах для определения формы и размеров геометрических фигур, для вычисления углов и для нахождения точек пересечения отрезков, лучей или прямых. Например, в задачах на геометрию можно использовать вершины треугольников или многоугольников для определения их свойств и решения задач на нахождение периметра, площади и других характеристик.

Что такое вершина в математике?

Вершина — это точка, в которой сходятся или от которой отходят отрезки, лучи или стороны геометрической фигуры.

Задачи с использованием вершин

Понимание понятия «вершина» в математике 4 класса играет важную роль в решении различных задач. Рассмотрим несколько примеров задач, в которых применяются вершины.

Пример 1:

У Маши есть треугольник с вершинами A, B и C. Она хочет найти периметр этого треугольника. Расстояние между вершинами A и B равно 5 см, между B и C — 4 см, а между A и C — 6 см. Какой будет периметр треугольника?

Решение:

Периметр треугольника равен сумме длин его сторон. В данном случае, стороны треугольника — это отрезки, соединяющие вершины A, B и C.

Суммируем длины сторон:

5 см + 4 см + 6 см = 15 см

Ответ: периметр треугольника равен 15 см.

Пример 2:

Вася и Петя стоят на разных вершинах прямоугольника ABCD. Вася на вершине A, а Петя на вершине C. Вася хочет дойти до вершины C, двигаясь только по сторонам прямоугольника. Сколько возможных путей может выбрать Вася?

Решение:

Чтобы добраться от вершины A до вершины C, Васе нужно пройти две стороны прямоугольника. Он может выбрать два пути: через вершину B или через вершину D.

Ответ: Вася может выбрать два пути.

Таким образом, использование вершин в математике 4 класса помогает решать различные задачи, связанные с геометрией и алгеброй. Знание понятия «вершина» и его применение позволяют развивать логическое мышление и умение анализировать геометрические объекты.

Свойства вершин

В математике вершиной называют точку, где пересекаются две или более прямых. Вершины могут иметь некоторые свойства, которые помогают нам лучше понять их характеристики.

1. Смежные вершины: Вершины, которые имеют общую сторону, называются смежными вершинами. Например, если у нас есть прямоугольник, то его углы будут смежными вершинами.

2. Вершины противоположных углов: В некоторых фигурах, таких как параллелограммы, вершины, которые находятся противоположно друг другу, называются вершинами противоположных углов.

3. Вершины равных углов: В некоторых фигурах, таких как квадраты или равнобедренные треугольники, вершины, которые образуют одинаковые углы, называются вершинами равных углов.

4. Вершины выпуклого и вогнутого многоугольника: Многоугольник, у которого все внутренние углы меньше 180 градусов, называется выпуклым многоугольником. Вершины такого многоугольника находятся на его внешней стороне. В многоугольнике, у которого есть углы больше 180 градусов, вершины находятся внутри многоугольника и такой многоугольник называется вогнутым.

Изучение свойств вершин помогает нам понимать геометрические фигуры и их характеристики. Эти свойства также могут использоваться для решения задач и построения геометрических конструкций.