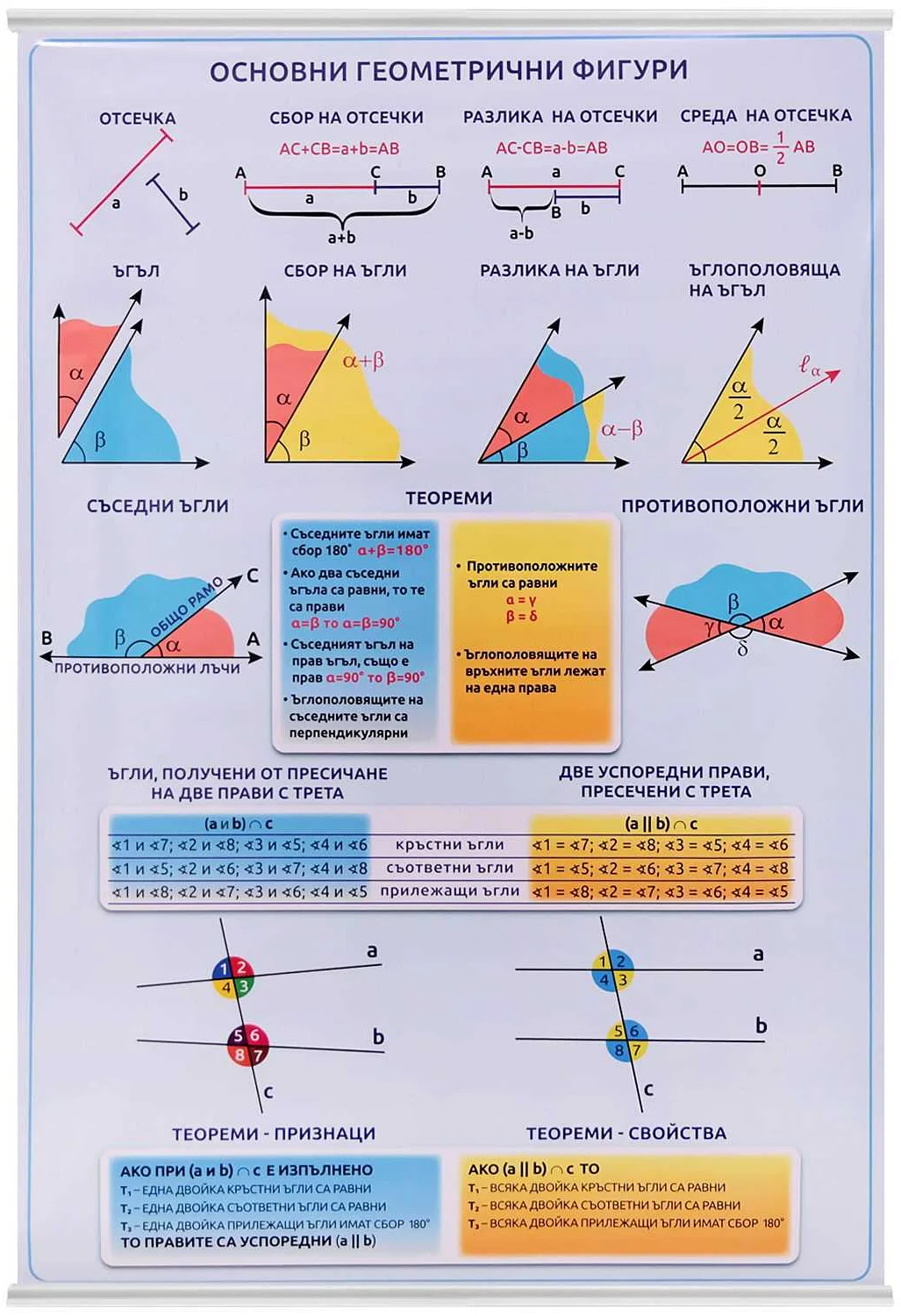
Назовите геометрическую фигуру которая является математической моделью колеса

Колесо — геометрическая фигура, представляющая собой математическую модель, используемую для описания формы и свойств колеса. В данной статье мы рассмотрим основные характеристики и свойства колеса как геометрической фигуры.

Колесо — одна из самых важных и распространенных геометрических фигур. Изначально колесо является круглой плоскостью, ограниченной одной закрытой кривой линией. Однако в математике колесо также может рассматриваться как двумерная или трехмерная модель с определенными параметрами и свойствами.

Колесо имеет множество применений и является основой для создания различных устройств и механизмов. Например, в транспорте колесо играет ключевую роль, обеспечивая передвижение автомобилей, велосипедов, поездов и других транспортных средств. Кроме того, колесо используется в различных механических системах, таких как шкивы, зубчатые колеса и многое другое.

В математике колесо также является объектом исследования и анализа. Оно имеет ряд интересных и полезных свойств, которые позволяют использовать его в решении различных задач. Например, колесо может быть использовано для моделирования движения и вращения, а также для анализа сил и моментов, действующих на объект.

Колесо — это не только геометрическая фигура, но и математическая модель, которая имеет широкий спектр применений и возможностей. Его изучение и анализ позволяют нам лучше понять и описать различные физические и механические процессы, происходящие в нашем мире.

История и применение колеса

История колеса начинается в древнейшие времена, примерно в 3500 году до нашей эры. В течение многих веков колесо использовалось в транспорте, сельском хозяйстве и промышленности.

В транспорте колесо стало основой для создания транспортных средств, таких как повозки, кареты, экипажи и велосипеды. Оно позволило значительно упростить передвижение людей и грузов, а также сократить время путешествия.

В сельском хозяйстве колесо использовалось для создания сельскохозяйственных орудий, таких как плуги и колесные телеги. Оно значительно облегчило работу фермеров и позволило увеличить производительность труда.

В промышленности колесо используется в различных машинах и механизмах, таких как фабричные станки, автомобили, поезда и самолеты. Оно является основой для создания движущихся механизмов и позволяет преодолевать дистанции с большой скоростью.

Сегодня колесо продолжает находить широкое применение в различных отраслях жизни. Оно является неотъемлемой частью транспорта, промышленности, сельского хозяйства и многих других сфер. Без колеса современная цивилизация была бы невозможна.

Геометрические параметры колеса

Один из основных параметров колеса — диаметр. Диаметр колеса — это расстояние между двумя противоположными точками на его окружности, проходящее через его центр. Диаметр обычно измеряется в единицах длины, таких как метры или дюймы.

Другим важным параметром колеса является радиус. Радиус колеса — это расстояние от его центра до любой точки его окружности. Радиус также измеряется в единицах длины и обычно равен половине диаметра.

Помимо диаметра и радиуса, для описания формы колеса используются такие параметры, как ширина обода, вылет и высота профиля. Ширина обода — это расстояние между двумя боковыми гранями колеса. Вылет — это расстояние от центра колеса до плоскости, проходящей через его ширины обода. Высота профиля — это расстояние от обода до плоскости, проходящей через центр колеса.

Знание геометрических параметров колеса важно для его правильной установки на автомобиль, а также для определения совместимости с другими деталями автомобиля.

Основные элементы колеса

1. Центр колеса — точка, которая находится в середине колеса и является его основным центром вращения. Центр колеса определяет его положение и движение.

2. Ось вращения — прямая линия, проходящая через центр колеса и вокруг которой оно вращается. Ось вращения определяет направление и скорость вращения колеса.

3. Обод колеса — внешняя окружность, образующая внешнюю границу колеса. Обод колеса является контактной точкой с поверхностью, по которой оно движется.

4. Диск колеса — внутренняя часть колеса, ограниченная ободом. Диск колеса обычно имеет специальное конструктивное назначение, например, крепление шины или механизмы тормозов.

5. Шина — внешняя оболочка колеса, которая обеспечивает его контакт с поверхностью и амортизацию. Шина может быть различной конструкции и материала в зависимости от цели использования колеса.

Все эти элементы вместе образуют колесо, которое является одним из основных инженерных решений для передвижения и переноски грузов.

Технологии производства колеса

1. Литье. Одним из наиболее распространенных методов производства колес является литье. В этом процессе металлический сплав или пластиковая смесь расплавляются и заливаются в специальные формы. После остывания и застывания материал принимает форму колеса. Такой метод позволяет создавать колеса различных форм и размеров.

2. Штамповка. Штамповка — это метод, при котором металлический лист прессуется под высоким давлением, чтобы придать ему форму колеса. Этот метод позволяет получить более точную форму и более высокую прочность колеса.

3. Обработка сталью. При производстве колес из стали применяется специальная обработка, которая придает колесу не только прочность, но и защищает его от коррозии. Обработка сталью может включать в себя термическую обработку, наплавку специальных покрытий и другие методы.

4. Композитные материалы. В последнее время стали популярны колеса из композитных материалов, таких как углепластик или алюминиевая смесь. Такие материалы обладают легкостью, прочностью и устойчивостью к коррозии, что делает колеса на их основе идеальными для использования в автомобильной и авиационной промышленности.

5. Обработка поверхности. Чтобы колесо имело гладкую поверхность и было приятным на ощупь, оно обрабатывается различными технологиями. Это может включать шлифовку, полировку, пескоструйную обработку и другие методы. Обработка поверхности также может включать нанесение специального покрытия для улучшения внешнего вида и защиты от воздействия окружающей среды.

Технологии производства колеса постоянно совершенствуются, что позволяет создавать колеса с высокими характеристиками и долгим сроком службы. Благодаря этому, колеса остаются важной составляющей многих транспортных средств и играют важную роль в нашей повседневной жизни.

Математическая модель колеса

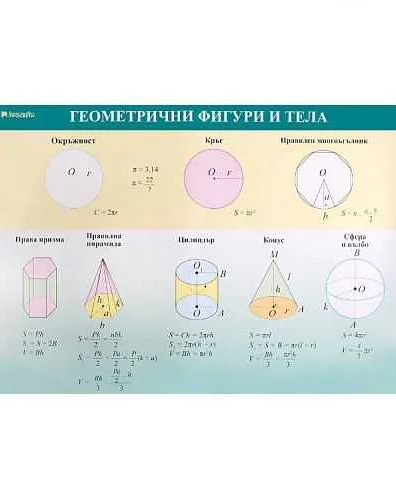
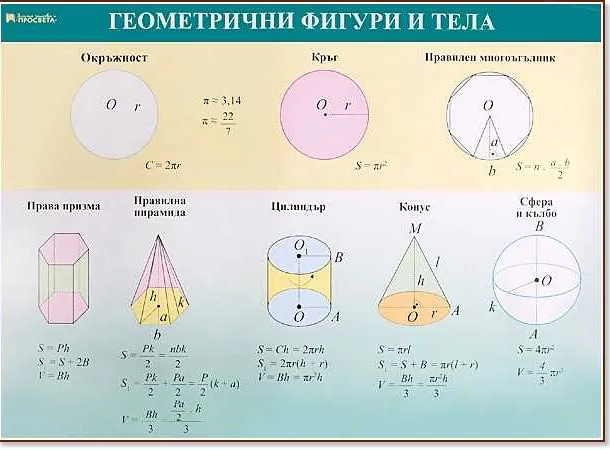
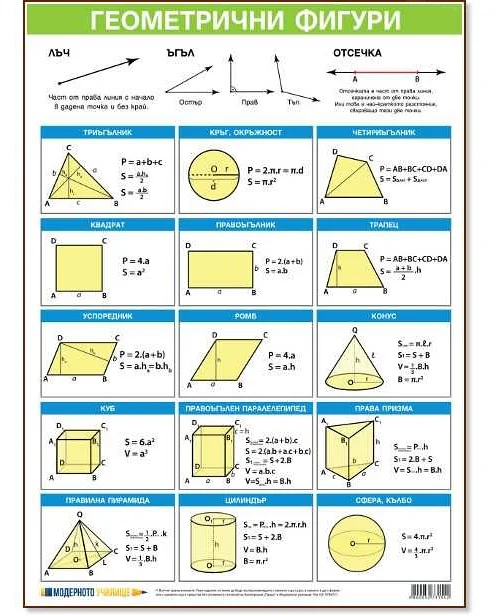
Одной из основных особенностей математической модели колеса является круговая форма. Круг является единственной геометрической фигурой, у которой все точки находятся на одинаковом расстоянии от центра. Именно поэтому колесо обычно моделируется как круг.

Радиус колеса — это расстояние от его центра до любой точки на его поверхности. Диаметр колеса — это двукратное значение радиуса, то есть расстояние между двумя противоположными точками на его поверхности. Площадь поверхности колеса можно рассчитать по формуле S = π * r^2, где S — площадь поверхности, π — математическая константа (приближенное значение 3.14159), r — радиус колеса. Объем колеса можно рассчитать по формуле V = π * r^2 * h, где V — объем, h — высота колеса.

Таким образом, математическая модель колеса позволяет анализировать его геометрические и физические характеристики, что является важным при разработке и тестировании колесных систем.

ПараметрОписаниеФормула

Радиус	Расстояние от центра колеса до любой точки на его поверхности	r
Диаметр	Расстояние между двумя противоположными точками на поверхности колеса	2r
Площадь поверхности	Площадь внешней поверхности колеса	S = π * r^2
Объем	Объем, занимаемый колесом	V = π * r^2 * h

Колесо в физике и механике

Во-первых, колесо используется в транспорте, таком как автомобили, велосипеды и самокаты. Колесо, вращаясь вокруг своей оси, позволяет передвигаться с меньшим усилием и сопротивлением. Это происходит благодаря меньшему трению, которое возникает при качении колеса по поверхности.

Во-вторых, колесо играет важную роль в механизмах, таких как шестеренки и зубчатые передачи. Оно используется для передачи и изменения механической энергии, обеспечивая эффективную работу различных механических устройств.

Кроме того, колесо также является ключевым компонентом в различных инерционных системах, таких как маховики и гироскопы. Оно обеспечивает стабильность и равновесие системы, а также позволяет сохранять угловой момент и кинетическую энергию.

Таким образом, колесо является неотъемлемой частью физики и механики. Оно обладает уникальными свойствами и применяется в различных областях науки и техники.

Видео по теме:

Вопрос-ответ:

Какая геометрическая фигура имеет форму колеса?

Колесо — это геометрическая фигура, которая имеет форму круга.

Какими математическими моделями можно описать колесо?

Колесо можно описать с помощью математической модели круга или с помощью модели окружности.

Какие свойства имеет колесо как геометрическая фигура?

Колесо обладает несколькими свойствами: оно является выпуклым многогранником, у него есть центр и радиус, а также диаметр и окружность.

Какие могут быть применения колеса в математике и физике?

Колесо имеет широкое применение в математике и физике. Например, оно используется для моделирования движения колесных транспортных средств, а также в качестве базовой фигуры для построения других геометрических объектов.

Как связаны колесо и круг?

Колесо и круг — это связанные понятия. Колесо является геометрической фигурой, имеющей форму круга, а круг является математической моделью колеса.

Что такое колесо?

Колесо — это геометрическая фигура, представляющая собой окружность, вращающуюся вокруг своей оси.

Колесо в транспорте и промышленности

Колесо играет важную роль в транспорте и промышленности, являясь неотъемлемой частью множества средств передвижения и механизмов.

В автомобильной промышленности колеса используются для обеспечения движения автомобиля по дороге. Они обеспечивают подвижность и устойчивость автомобиля, позволяя ему преодолевать препятствия и различные типы поверхностей.

Колеса также широко применяются в железнодорожном транспорте. Вагоны и поезда оснащены колесами, которые обеспечивают плавность движения по рельсам. Колеса железнодорожных транспортных средств имеют специальную конструкцию, позволяющую им преодолевать большие расстояния и выдерживать высокие нагрузки.

В промышленности колеса применяются в различных механизмах и машинах. Они могут быть использованы для передвижения грузовых платформ, поддержки и перемещения тяжелых предметов, а также для поворота различных механических устройств.

Колеса также используются в сельском хозяйстве. Они могут быть установлены на сельскохозяйственные машины, такие как тракторы, комбайны и другие сельскохозяйственные транспортные средства, облегчая работу на поле и увеличивая эффективность процесса.

ПрименениеПримеры

Автомобильная промышленность	Легковые автомобили, грузовики, автобусы
Железнодорожный транспорт	Поезда, вагоны, метро
Промышленность	Механизмы, машины, грузоподъемное оборудование
Сельское хозяйство	Тракторы, комбайны, сельскохозяйственные машины

Колесо является одним из ключевых элементов в транспортной и промышленной сфере, обеспечивая эффективность и безопасность в различных ситуациях и условиях использования.

Современные тенденции в развитии колеса

С развитием технологий и научных исследований, колесо продолжает эволюционировать и совершенствоваться.

Одной из главных тенденций в развитии колеса является повышение его эффективности и улучшение производительности. Специалисты стремятся создать колеса, которые обладают меньшими сопротивлением качению, чтобы улучшить тяговые характеристики транспортных средств. Это особенно важно для автомобильной промышленности, где каждый процент снижения сопротивления может привести к существенной экономии топлива.

Еще одной важной тенденцией является разработка более прочных и долговечных материалов для колес. Современные материалы, такие как карбоновые волокна или сплавы, позволяют создавать колеса, которые выдерживают большие нагрузки и долго сохраняют свои характеристики. Это особенно актуально для колес транспортных средств, которые подвергаются значительным механическим воздействиям.

Также в последние годы наблюдается увеличение использования колес с аэродинамическими свойствами. Модели с улучшенной аэродинамикой помогают снизить сопротивление воздуха и улучшить скоростные характеристики транспортных средств. Это особенно важно для гоночных автомобилей или велосипедов, где каждая доля секунды имеет значение.

ТенденцияПримеры

Повышение эффективности	Снижение сопротивления качению
Улучшение прочности	Использование карбоновых волокон и сплавов
Аэродинамические свойства	Модели с улучшенной аэродинамикой

Все эти тенденции направлены на создание более эффективных, прочных и инновационных колес, которые удовлетворяют современным требованиям транспортной и промышленной отраслей.