Зачем изучать математические методы теории колебаний: примеры применения и польза для практики

Изучение математических методов теории колебаний важно для понимания интерактивных систем, кроме того, это помогает в решении практических задач на производстве и повседневной жизни. Приобретение знаний в этой области поможет вам развить новые навыки и улучшить качество решаемых задач.

Математические методы теории колебаний имеют огромное значение как в научных исследованиях, так и в практической деятельности. Они используются в широком спектре приложений, начиная от механики и электроники и заканчивая сферами медицины и экономики. В этой статье мы рассмотрим, почему изучение математических методов теории колебаний настолько важно для этих областей, и как они могут повысить эффективность и точность исследований и прогнозов.

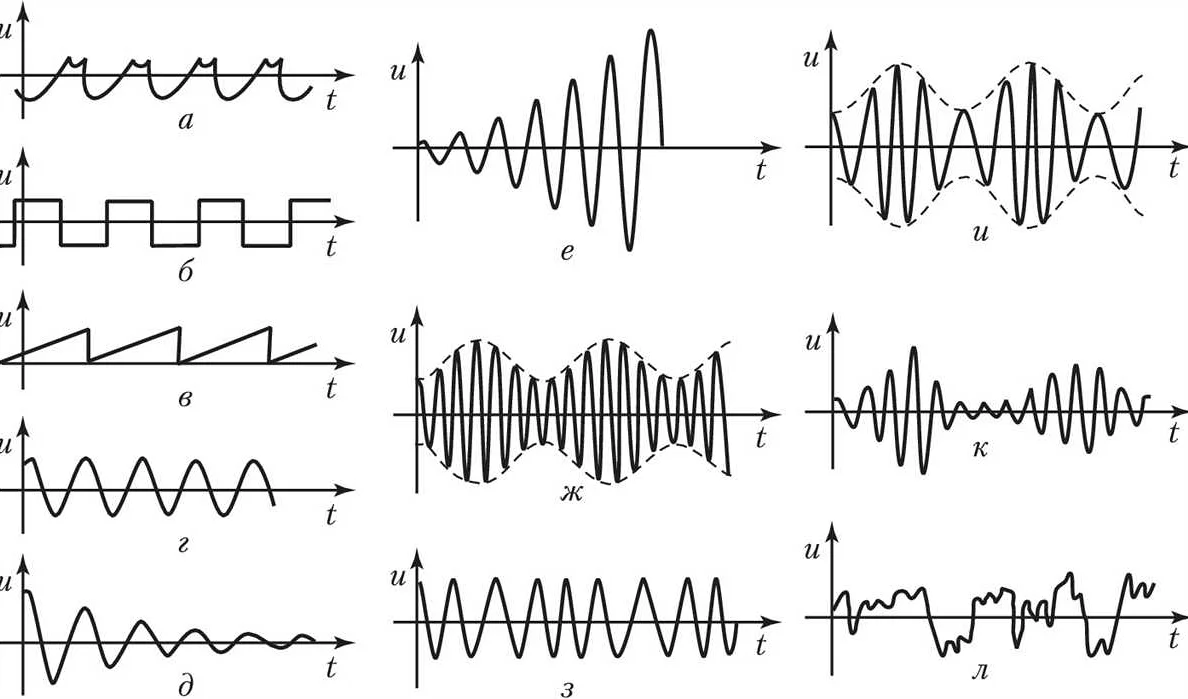
Колебания – это явление, которое возникает во многих системах и является одним из важнейших аспектов многих технических и научных дисциплин. Колебания могут быть как действительными, так и воображаемыми, но все они обладают характерными свойствами, которые могут быть описаны математически. Таким образом, язык математики становится необходимым для понимания и анализа колебательных процессов, который можно использовать для получения более точных и более полных данных о системах, подверженных колебаниям.

С помощью математических методов теории колебаний мы можем производить математическое моделирование систем, которые подвержены колебаниям, и проводить теоретический анализ колебательных процессов. Это помогает выявить слабости в системах и предсказывать, как они будут вести себя в будущем. Таким образом, изучение математических методов теории колебаний позволяет нам улучшить прогнозирование, что имеет важное значение для различных отраслей науки и промышленности.

Применение математических методов в различных областях науки и техники

Математические методы теории колебаний используются в широком спектре областей науки и техники. Например, в авиастроении математические методы применяются для моделирования динамики полета самолетов и проектирования автопилотов. Математика также играет важную роль в разработке компьютерных игр и визуализации данных.

Инженеры и ученые используют математику для прогнозирования погоды и климата, а также при разработке электрических и механических систем. В медицине математические модели помогают понять физиологические процессы, разработать новые методы лечения и диагностики заболеваний.

Математика также важна в области финансов и экономики, где она используется для анализа рыночных данных и прогнозирования трендов. В криптографии, математические методы используются для защиты данных и разработки безопасных систем связи.

В искусственном интеллекте, математические алгоритмы применяются для обучения систем распознаванию образов и речи, а также для создания более эффективных и автоматизированных процессов.

В целом, математические методы и теория колебаний играют важную роль в практически всех областях науки и техники, помогая ученым и инженерам решать сложные проблемы и разрабатывать новые и инновационные технологии и решения.

Понимание основных понятий теории колебаний

Теория колебаний является одной из важнейших областей математики, физики и инженерных наук, которая занимается изучением колебательных процессов в различных аспектах.

Колебания – это движения, которые приводят к чередованию изменений величин, например, изменению положения, скорости или ускорения. Они могут возникать как в механических системах, так и в термодинамических, электрических и других системах.

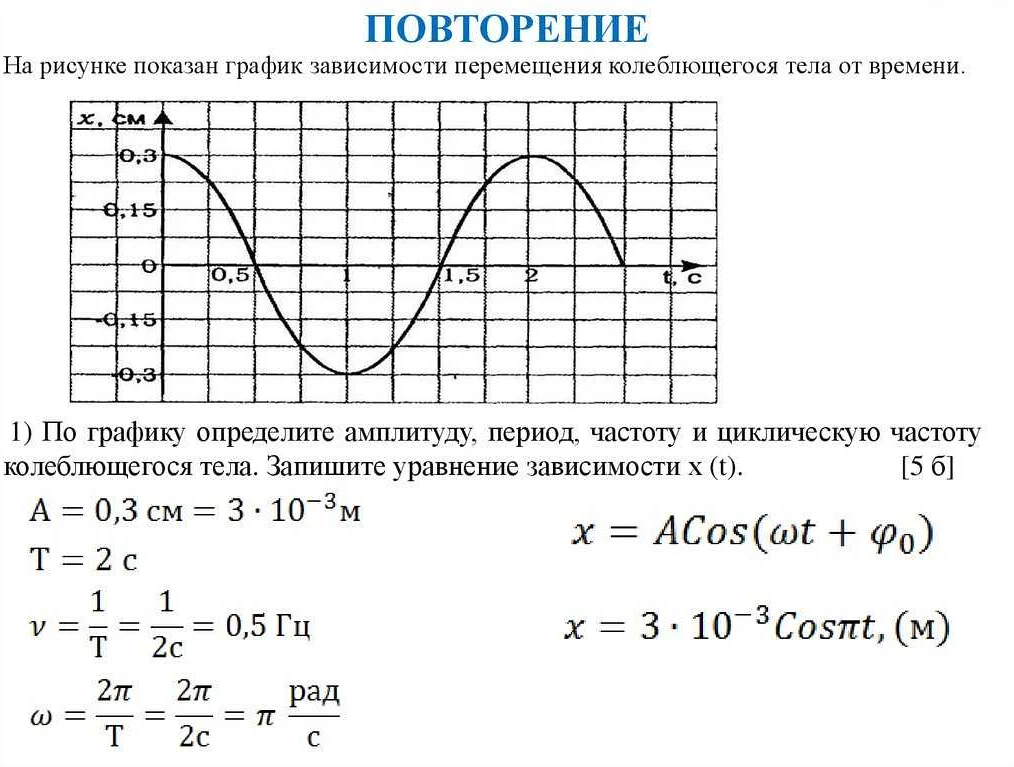
Основными понятиями, которые изучает теория колебаний, являются амплитуда, период, частота, фаза и добротность.

• Амплитуда – максимальное отклонение колеблющейся величины от ее равновесного положения.
• Период – время, за которое колеблющаяся величина выполняет один полный цикл своего движения.
• Частота – количество циклов, которые производит колеблющаяся величина в единицу времени.
• Фаза – сдвиг колебаний относительно начального момента времени.
• Добротность – мера затухания колебаний за один период.

Понимание этих понятий важно для решения многих прикладных задач, таких как нахождение резонансных условий, определение параметров систем, отслеживание динамических изменений.

Анализ гармонических колебаний

Гармонические колебания являются одним из наиболее распространенных и изучаемых типов колебаний. В их основе лежит простейшее гармоническое движение, при котором тело движется синусоидально вокруг своей средней позиции.

Анализ гармонических колебаний в математике является важным инструментом для решения различных физических задач, таких как колебания механических систем, электрических цепей, оптических систем и др. Он позволяет нам представлять колебания в виде математических функций, что позволяет использовать вычислительные методы и найти аналитические решения.

С помощью анализа гармонических колебаний можно изучать различные параметры колебательной системы, такие как амплитуда, частота, фаза, период и др. Благодаря этому можно оптимизировать работу системы, улучшить ее параметры и добиться наибольшей эффективности.

Одним из примеров применения анализа гармонических колебаний может служить исследование акустических систем. С помощью математических методов можно определить оптимальные параметры для акустических систем, добиться максимальной чувствительности на определенных частотах и обеспечить высокое качество звука.

Изучение амплитудных и фазовых характеристик колебательной системы

Студенты, изучающие математические методы теории колебаний, знакомятся с амплитудными и фазовыми характеристиками колебательных систем. Эти характеристики позволяют определить, как изменяется амплитуда и фаза колебаний в зависимости от различных параметров системы.

Амплитудная характеристика колебательной системы определяет зависимость амплитуды колебаний от частоты внешнего воздействия. Изучение этой характеристики позволяет определить резонансные значения частоты воздействия, при которых амплитуда колебаний наибольшая.

Фазовая характеристика колебательной системы определяет зависимость начальной фазы колебаний от частоты внешнего воздействия. Изучение этой характеристики позволяет определить, как изменяется фазовый сдвиг между внешним воздействием и колебаниями в зависимости от частоты воздействия.

Изучение амплитудных и фазовых характеристик колебательной системы является важным для практики, так как позволяет определить наилучшую конфигурацию системы и достичь максимального эффекта при ее использовании. Например, в инженерии это может быть применено при создании колебательных систем в автомобиле, ихроне, самолете или другом транспортном средстве.

Расчет параметров механических и электрических колебательных систем

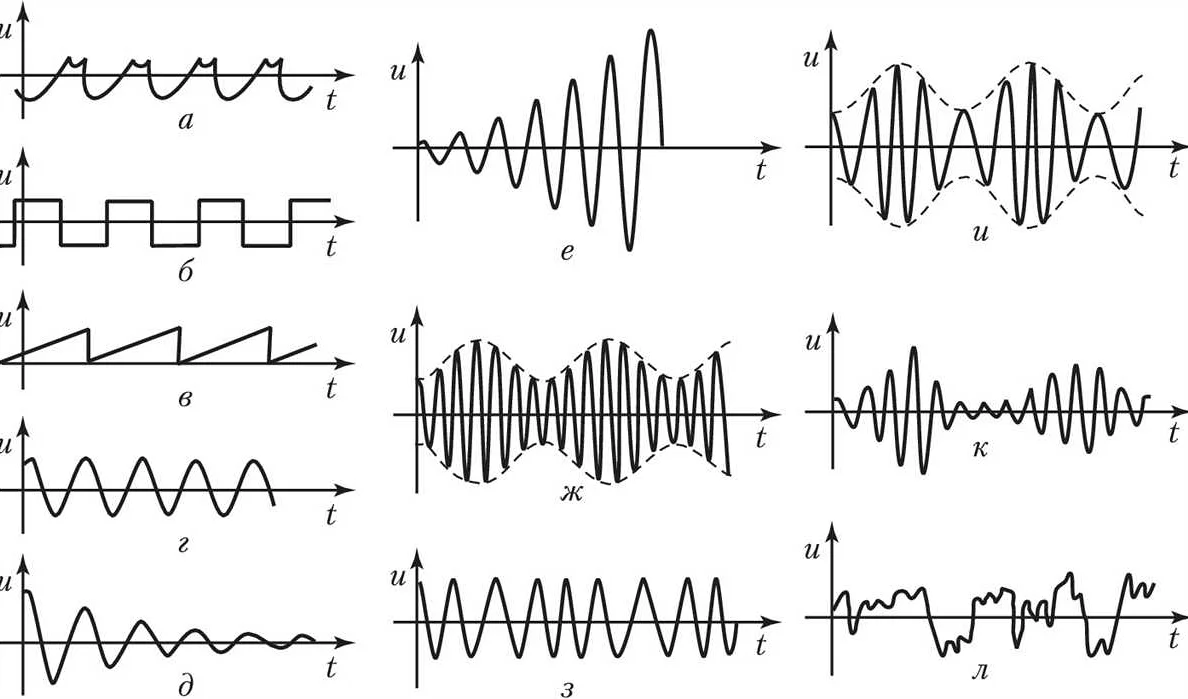
Для эффективной работы с механическими и электрическими колебательными системами важно иметь представление о характеристиках этих систем. Расчет параметров колебательной системы позволяет определить ее резонансную частоту, амплитуду колебаний, период колебаний, а также другие важные характеристики.

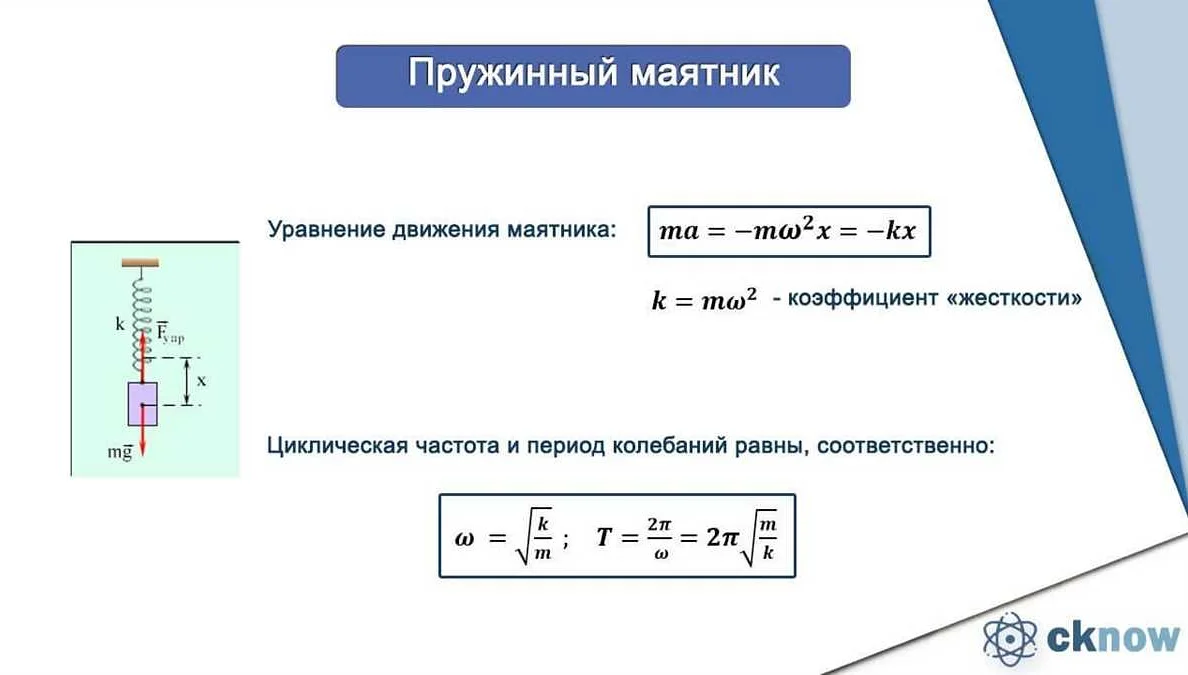
Для расчета параметров механической колебательной системы необходимо знать ее массу, коэффициент жесткости и коэффициент демпфирования. На основе этих данных можно определить ее собственную частоту, амплитуду колебаний и период колебаний. Расчет параметров электрической колебательной системы также требует определенных параметров, таких как ёмкость конденсатора, индуктивность катушки и сопротивление. Исходя из этих параметров можно определить резонансную частоту, амплитуду и период колебаний.

Расчет параметров механической и электрической колебательной системы важен для создания различных устройств, таких как маятники, кварцевые часы, беспроводные передатчики, радиоприемники и многое другое. Без понимания и определения параметров колебательной системы невозможно создать эффективное и качественное устройство, работающее на колебательном принципе.

Исследование нелинейных колебаний

Изучение нелинейных колебаний имеет огромное значение для решения реальных инженерных задач. В отличие от линейных колебаний, где существует линейная зависимость между силой и перемещением, нелинейные колебания не могут быть описаны линейными уравнениями. В то же время, большинство инженерных конструкций испытывают нелинейные колебания на практике.

Это может быть связано с различными факторами, такими как неоднородность материала, физические нелинейности, взаимодействие структурных компонентов и другие. Изучение нелинейных колебаний помогает инженерам более точно оценить поведение конструкций, увеличить их срок службы и предотвратить потенциальные аварийные ситуации.

Математические методы теории нелинейных колебаний позволяют решать различные задачи, связанные с динамикой конструкций. Например, можно определить собственные формы колебаний и частоты системы, исследовать устойчивость рабочего режима или описать динамику конструкции при изменении параметров окружающей среды.

Также изучение нелинейных колебаний позволяет эффективно применять методы моделирования и численного анализа при проектировании и исследовании конструкций. Инженеры могут использовать математические модели для определения влияния различных факторов на работу системы и выбора оптимальных параметров для достижения желаемых результатов.

Разбор задач на колебания с несколькими степенями свободы

Колебания с несколькими степенями свободы – это колебания системы, которая имеет несколько степеней свободы. Такие системы могут быть определены с помощью уравнений, в которых присутствуют несколько переменных.

Разбор задач на колебания с несколькими степенями свободы может быть сложным процессом, который требует от студента не только теоретических знаний, но также и практического опыта. Для успешного решения задач необходимо иметь глубокое понимание физических и математических аспектов механики колебательных систем.

Существует несколько методов решения задач на колебания с несколькими степенями свободы, которые включают в себя методы аналитического решения, численные методы и методы приближений. Аналитические методы позволяют получить точное решение, но часто требуют высокого уровня математической подготовки. Численные методы используются для решения задач, которые невозможно решить аналитически, и представляют собой алгоритмы вычисления решения на компьютере. Методы приближений позволяют получить решение задачи, которое близко к точному, но требуют меньших затрат времени и усилий.

1. Важной частью разбора задач на колебания с несколькими степенями свободы является построение дифференциальных уравнений, описывающих движение системы.
2. Затем следует найти характеристический полином системы, который определяет угловую частоту колебаний в системе.
3. Далее, нужно найти собственные векторы и собственные значения матрицы системы, которые позволяют определить форму колебаний в системе.
4. Наконец, на основе этих результатов можно определить амплитуды и фазы колебаний, а также графически изобразить движение системы в пространстве.

Разбор задач на колебания с несколькими степенями свободы является важной частью обучения механики колебательных систем, которая имеет большое практическое значение. Он представляет собой сложный, но увлекательный процесс, который требует от студента усидчивости, терпения и логического мышления.

Определение собственных частот колебательной системы

Собственные частоты колебательной системы являются ключевым параметром, определяющим ее поведение и структуру. Они описывают частоты, при которых система колеблется с минимальной амплитудой и без внешних воздействий.

Определение собственных частот является задачей, которую можно решить с помощью математических методов теории колебаний. Для этого необходимо решить уравнение движения системы с начальными условиями. Результатом решения будут значений частот, при которых система может колебаться в естественном режиме.

Знание собственных частот позволяет предсказывать поведение и реакцию системы на внешние воздействия. Например, при исследовании зданий и сооружений, знание собственных частот позволяет определить оптимальный режим работы и установить необходимые меры для предотвращения разрушений.

Таким образом, определение собственных частот колебательной системы является важным этапом в исследовании и проектировании технических объектов, применяемых в различных отраслях науки и производства.

Проектирование колебательных систем

Математические методы теории колебаний являются полезными для проектирования колебательных систем. Они позволяют оценить параметры системы, такие как период, амплитуду колебаний, частоту и фазу. Эти параметры могут быть использованы для оптимизации системы и достижения желаемых характеристик.

Проектирование колебательных систем является важным для многих приложений, включая резонансные контуры, электрические цепи, механические системы и даже биологические системы. Математические методы теории колебаний могут помочь улучшить производительность или даже предотвратить сбои в системах.

Одним из методов проектирования колебательных систем является анализ частотной характеристики. Данные по частотной характеристике могут быть использованы для настройки системы на желаемый диапазон частот. Это может быть важно для многих приложений, включая звуковые усилители и радиопередатчики.

Еще один метод проектирования колебательных систем — это анализ амплитудно-частотной характеристики. Этот метод может быть использован для определения амплитуды колебаний в зависимости от частоты и может помочь избежать резонанса в системе, что может привести к ее разрушению.

Кроме того, математические методы могут быть использованы для анализа динамической стабильности системы. Этот анализ может помочь определить, насколько устойчива колебательная система к малым изменениям параметров.

В целом, математические методы теории колебаний играют важную роль в проектировании колебательных систем. Они позволяют предсказывать и оптимизировать различные параметры системы и помогают улучшить ее производительность и устойчивость.

Расчет и моделирование динамических процессов в инженерных системах

Математические методы теории колебаний являются важным инструментом для расчета и моделирования динамических процессов в различных инженерных системах. Они позволяют оценивать поведение системы, определять ее резонансные частоты и предсказывать ее поведение при различных условиях.

Также, математические методы теории колебаний используются для анализа и проектирования различных систем контроля и стабилизации. Они помогают определять параметры контроллеров, оценивать их производительность и предсказывать реакцию системы на внешние возмущения и изменения параметров.

Математические методы теории колебаний также широко используются в различных областях машиностроения, электроники, авиации и других отраслях. Они помогают оптимизировать производственные процессы, улучшить качество продукции и повысить безопасность эксплуатации систем.

В целом, изучение математических методов теории колебаний является важным для практического применения в инженерных системах и позволяет улучшить их производительность, надежность и безопасность.

Оптимизация работы технических устройств с помощью теории колебаний

Современные технические устройства, начиная от автомобилей и заканчивая космическими аппаратами, работают на основе механических колебаний. Поэтому понимание и математическое описание процессов колебаний является необходимым условием для оптимизации работы технических устройств. Оптимальное снижение вибраций не только повышает эффективность работы механизмов, но и увеличивает их срок службы, а также снижает уровень шума и вибрации, что важно для комфорта людей вблизи устройств.

Одним из наиболее важных инструментов оптимизации механических систем является теория колебаний. Эта теория позволяет анализировать механические системы и оценивать их работу в условиях различных воздействий. Кроме того, она помогает исследовать динамические свойства материалов, что в свою очередь, позволяет улучшать их качество и увеличивать их прочность.

Таким образом, знание математических методов теории колебаний является необходимым для инженеров, разрабатывающих технические устройства. Они могут использовать эти знания для улучшения конструкций своих устройств, повышения их эффективности и долговечности. Также они смогут учесть влияние колебаний на окружающую среду и обеспечить безопасность работы устройств.

Вопрос-ответ:

Какую роль играют математические методы в теории колебаний?

Математические методы являются основой теории колебаний. Без математической формализации колебаний мы бы не смогли предсказать поведения системы при колебательных процессах и не смогли бы применять эту теорию для решения практических задач.

Какие математические методы применяются в теории колебаний?

В теории колебаний применяются методы математического анализа, линейной алгебры, дифференциальных уравнений, теории функций комплексного переменного, вероятностных и статистических методов и др.

Какую практическую значимость имеют математические методы теории колебаний?

Математические методы теории колебаний позволяют решать множество практических задач: от проектирования инженерных систем и оптимизации их параметров до анализа и прогнозирования поведения технических устройств в различных условиях эксплуатации.

Какова связь между математическими методами и экспериментальными данными в теории колебаний?

Математические методы теории колебаний позволяют на основе экспериментальных данных получить математическую модель системы, описывающую ее колебательное поведение. Затем с помощью этой модели можно решать задачи, которые не были решимы экспериментально.

Какие проблемы можно решать с помощью математических методов теории колебаний?

Математические методы теории колебаний позволяют решать множество задач, связанных с колебаниями различных систем. Например, можно рассчитывать собственные частоты и формы колебаний, оптимизировать параметры системы, анализировать устойчивость, описывать и прогнозировать динамическое поведение системы во времени и т.д.

Каково значение математических методов теории колебаний в современных технологиях?

Математические методы теории колебаний имеют огромное значение для современных технологий, которые используют колебания во множестве своих приложений: от электроники и авиации до медицины и экономики. Без математической формализации колебаний современный прогресс был бы недостижим.

Насколько сложны математические методы теории колебаний?

Математические методы теории колебаний могут быть очень сложными и требовать глубоких знаний математики. В тоже время, некоторые аспекты теории колебаний можно понять и использовать с помощью элементарной математики. Однако, для того чтобы решать сложные задачи, важно иметь хорошие знания и умения в математике.

Видео по теме: