Что значит п в математике большая буква

В математике большая буква ‘п’ обозначает пространство или множество, которое может содержать элементы или явления с общими свойствами. Узнайте, как применяется п в различных областях математики и какие конкретные значения оно может иметь.

Буква «П» в математике играет важную роль, обозначая различные понятия и операции. Она используется для обозначения числа «пи» (π) — одной из самых известных и важных математических констант. Значение «пи» равно отношению длины окружности к ее диаметру и приближенно равно 3,14159. «Пи» является иррациональным числом, что означает, что его десятичное представление не имеет конечной последовательности цифр и не повторяется.

Буква «П» также используется для обозначения вероятности (P) — одного из основных понятий теории вероятностей. Вероятность показывает, насколько вероятно возникновение события из некоторого множества возможных событий. Она измеряется числом от 0 до 1, где 0 означает невозможность события, а 1 — его полную уверенность. Промежуточные значения указывают на степень вероятности события.

Буква «П» также обозначает перестановку (P) — одну из основных операций в комбинаторике. Перестановка — это упорядоченное расположение элементов множества. Для множества из n элементов количество различных перестановок равно n! (n факториал). Например, для множества из 3 элементов существует 3! = 3 * 2 * 1 = 6 различных перестановок.

Буква «П» также используется для обозначения пространства вероятностей в теории вероятностей. Пространство вероятностей — это множество всех возможных исходов случайного эксперимента. Обозначается оно символом Ω (омега) или P (прописная пи). Пространство вероятностей является основой для определения вероятностей различных событий и выполнения операций над ними.

Значение буквы «П» в математике

Буква «П» в математике имеет несколько значений и используется для обозначения различных понятий.

Одним из наиболее распространенных значений буквы «П» является обозначение математической константы «Пи» (π). «Пи» является одним из наиболее важных математических постоянных и используется для вычисления длины окружности, площади круга и других геометрических параметров. Значение «Пи» приближенно равно 3,14159.

Также буква «П» может использоваться для обозначения вероятности (P). Вероятность является одним из основных понятий теории вероятностей и используется для измерения степени достоверности событий. Значение вероятности находится в промежутке от 0 до 1, где 0 означает полную невозможность события, а 1 — его полную достоверность.

Кроме того, буква «П» может обозначать периметр (P) геометрической фигуры, такой как прямоугольник или треугольник. Периметр представляет собой сумму длин всех сторон фигуры и используется для вычисления ее общей длины.

ОбозначениеЗначениеПрименение

π	3,14159	Вычисление геометрических параметров окружности и круга
P	0 ≤ P ≤ 1	Измерение вероятности событий
P	Сумма длин сторон фигуры	Вычисление периметра геометрической фигуры

Видео по теме:

Основные понятия

В математике буква «П» используется для обозначения различных понятий и операций. Ниже приведены основные из них:

• Периметр — это сумма длин всех сторон геометрической фигуры. Обычно обозначается буквой «П» с индексом, указывающим на конкретную фигуру, например «Пк» для квадрата или «Птр» для треугольника.
• Площадь — это мера двумерной поверхности геометрической фигуры. Обозначается также буквой «П» с индексом, например «Пк» для квадрата или «Птр» для треугольника.
• Произведение — это операция умножения двух или более чисел. В математике обозначается символом «×» или «.». Например, «3 × 4» означает произведение чисел 3 и 4.
• Предел — это концепция, используемая в математическом анализе для определения предельного значения функции или последовательности. Обозначается с помощью символа «lim» и часто используется вместе с буквой «П», например «lim П→∞».

Это лишь некоторые из основных понятий, связанных с буквой «П» в математике. Она имеет множество других применений и значений в различных областях математики.

Применение буквы «П»

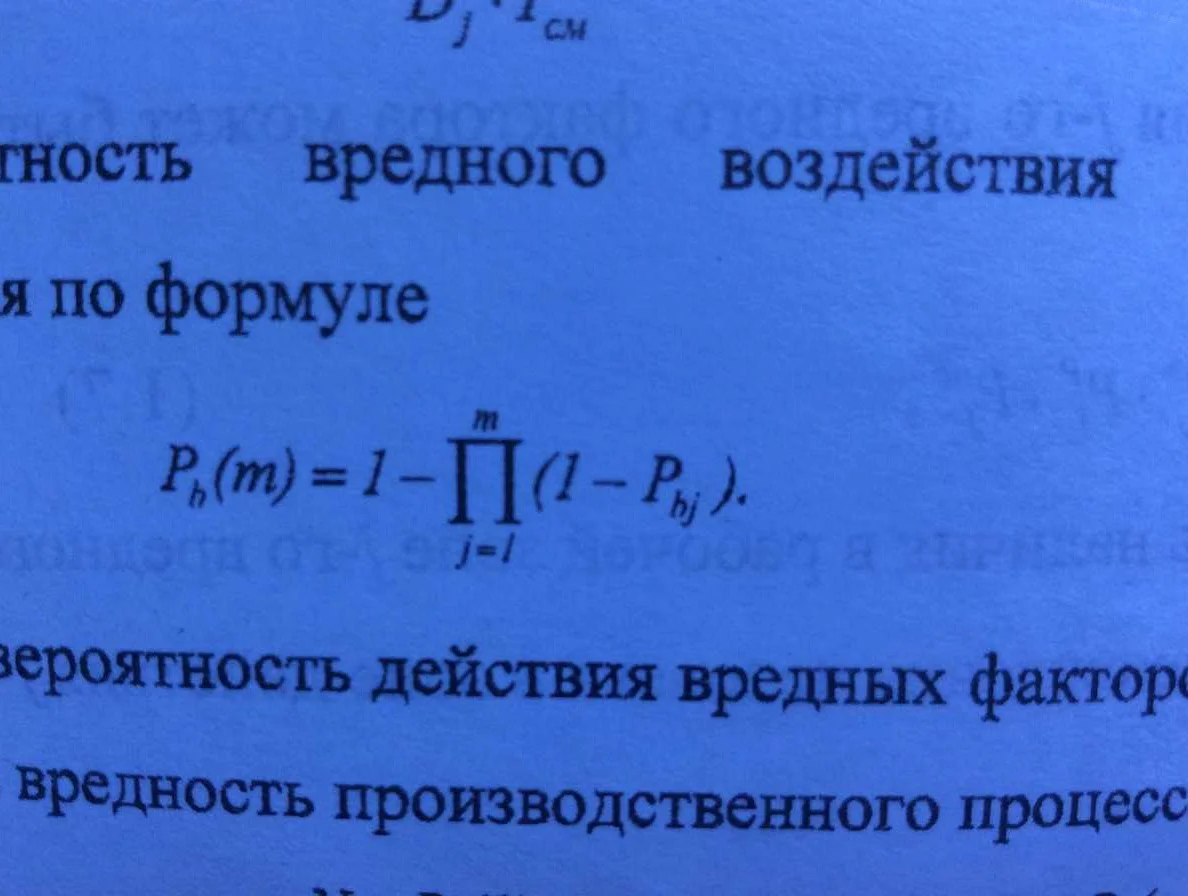
Буква «П» в математике используется для обозначения различных понятий и операций.

Одним из основных применений буквы «П» является обозначение периметра. Периметр — это сумма длин всех сторон геометрической фигуры. Например, для прямоугольника периметр вычисляется по формуле P = 2a + 2b, где a и b — длины сторон.

Буква «П» также используется для обозначения вероятности. Вероятность — это числовая характеристика, отражающая степень достоверности наступления события. Вероятность обычно выражается дробью от 0 до 1, где 0 — событие невозможно, а 1 — событие обязательно. Например, P(A) обозначает вероятность наступления события A.

Также буква «П» используется для обозначения математического ожидания. Математическое ожидание — это среднее значение случайной величины, которое показывает, какое значение можно ожидать в среднем. Например, математическое ожидание случайной величины X обозначается как E(X) или P(X).

Буква «П» также может использоваться для обозначения других понятий и переменных в математике, в зависимости от контекста.

Вопрос-ответ:

Какое значение может иметь буква «П» в математике?

В математике буква «П» может иметь различные значения в зависимости от контекста. Одним из основных значений является обозначение вероятности события.

Какие понятия связаны с буквой «П» в математике?

Буква «П» в математике связана с такими понятиями, как периметр, площадь, пространство, пропорция, пуассоновское распределение, параметр и многими другими.

Как применяется буква «П» в математике?

Буква «П» применяется в математике для обозначения различных величин и понятий. Например, в геометрии она используется для обозначения периметра и площади фигур, а в теории вероятностей — для обозначения вероятности события. Также буква «П» встречается в формулах и уравнениях, где она обозначает параметр или пространство.

Какую роль играет буква «П» в пуассоновском распределении?

В пуассоновском распределении буква «П» обозначает параметр, который представляет собой среднее количество событий, происходящих в единицу времени или пространства. Она определяет форму и характеристики распределения.

Понятие «Парабола»

Парабола имеет особенные свойства, которые широко применяются в математике и физике. Она является симметричной относительно оси, проходящей через фокус и перпендикулярной директрисе. Также парабола является графиком квадратичной функции, имеющей уравнение вида y = ax^2 + bx + c, где a, b и c — коэффициенты, определяющие форму, положение и ориентацию параболы.

Параболы широко используются в физике для моделирования траекторий движения объектов, таких как снаряды или планеты под воздействием гравитационных сил. Они также встречаются в оптике, где параболические зеркала используются для фокусировки света и создания изображений.

Изучение параболы и ее свойств играет важную роль в математическом анализе, геометрии и алгебре. Оно позволяет анализировать и решать различные задачи, связанные с кривыми и функциями в общем.

Определение параболы

При определении параболы используются следующие термины:

• Фокус — точка, относительно которой определяется парабола. Она обозначается буквой «F».
• Директриса — прямая, относительно которой определяется парабола. Она обозначается буквой «d».
• Вершина — точка, являющаяся пересечением параболы и оси симметрии. Она обозначается буквой «V».
• Ось симметрии — прямая, проходящая через фокус и перпендикулярная директрисе. Она обозначается буквой «O».

Парабола имеет следующие свойства:

1. Все точки параболы равноудалены от фокуса и директрисы.
2. Фокус и директриса находятся на одном перпендикуляре к оси симметрии параболы.
3. Расстояние от фокуса до вершины параболы равно расстоянию от вершины до директрисы.

Параболы широко используются в математике и физике для моделирования различных явлений и процессов.

Свойства параболы

У параболы есть несколько важных свойств:

• Фокус и директриса: парабола имеет фокус и директрису. Фокус — это точка F на параболе, к которой все точки параболы имеют одинаковое расстояние. Директриса — это прямая, к которой все точки параболы имеют одинаковое расстояние.
• Отражающее свойство: парабола имеет отражающее свойство, что означает, что любой луч, отраженный от параболы, проходит через фокус. Это свойство часто используется в оптике.
• Симметрия: парабола симметрична относительно своей оси симметрии, которая проходит через фокус и перпендикулярна директрисе.
• Вершина: вершина параболы — это точка, в которой парабола достигает своего максимума или минимума.
• Устремление к бесконечности: парабола стремится к бесконечности, но никогда не достигает ее.

Свойства параболы играют важную роль в различных областях, таких как физика, инженерия и архитектура. Изучение параболы позволяет решать множество задач, связанных с графиками и уравнениями.

Понятие «Площадь»

Площадь обычно выражается в квадратных единицах, таких как квадратные метры (м^2) или квадратные сантиметры (см^2).

Для различных геометрических фигур, таких как прямоугольник, квадрат, треугольник, круг и другие, существуют специальные формулы для вычисления площади.

Например, площадь прямоугольника можно вычислить, умножив длину на ширину:

Площадь прямоугольника = Длина * Ширина

А площадь круга можно вычислить по формуле:

Площадь круга = Пи * Радиус^2

Знание понятия площади позволяет решать множество задач в геометрии и других областях математики, а также имеет широкое практическое применение в повседневной жизни, например, при планировании строительства, измерении площади земли, расчете площади комнат и т.д.

Определение площади

Для различных геометрических фигур существуют специальные формулы для расчета площади. Например, для прямоугольника площадь вычисляется как произведение длины одной из его сторон на длину другой стороны.

Важно отметить, что площадь является величиной неотрицательной и измеряется в квадратных единицах длины, таких как квадратные метры, квадратные сантиметры и т. д.

Знание понятия площади и умение вычислять ее для различных фигур является важным при изучении геометрии, а также находит свое применение в других областях, таких как архитектура, строительство, дизайн и т. д.

Формулы для вычисления площади

1. Площадь прямоугольника:

Для вычисления площади прямоугольника необходимо умножить длину одной его стороны на длину другой:

S = a * b

2. Площадь треугольника:

Площадь треугольника можно вычислить по формуле, используя длину основания и высоту:

S = (a * h) / 2

3. Площадь круга:

Площадь круга можно вычислить по формуле, используя радиус:

S = π * r^2

4. Площадь параллелограмма:

Площадь параллелограмма можно вычислить, умножив длину основания на высоту:

S = a * h

5. Площадь трапеции:

Площадь трапеции можно вычислить по формуле, используя сумму оснований и высоту:

S = ((a + b) * h) / 2

Зная данные фигуры, можно использовать соответствующую формулу для вычисления их площади. Это позволяет находить площадь различных поверхностей и решать задачи, связанные с измерениями и расчетами.

Понятие «Производная»

Производная обозначается символом «П» и записывается как f'(x) или dy/dx, где f — функция, а x — независимая переменная. Определение производной основано на пределе, и она может быть вычислена для различных типов функций, включая алгебраические, тригонометрические, экспоненциальные и логарифмические.

Производная имеет много практических применений в различных областях науки и техники. Например, она используется для определения скорости изменения физических величин, таких как расстояние, время, температура и давление. Также производная позволяет находить точки экстремума функций и строить графики функций.

Понимание производной является основой для изучения более сложных понятий, таких как интегралы, дифференциальные уравнения и теория вероятностей. Поэтому владение этим понятием является важным для успешного изучения математики и её приложений.