Что значит двоеточие в математике
Содержимое
- 1 Что значит двоеточие в математике
- 1.1 Определение двоеточия в математике
- 1.2 Использование двоеточия для обозначения отношений
- 1.3 Использование двоеточия в графиках и таблицах
- 1.4 Использование двоеточия в пропорциях и долях
- 1.5 Использование двоеточия в выражении условий
- 1.6 Использование двоеточия в функциях и формулах
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Какое значение имеет двоеточие в математике?
- 1.8.0.2 Как можно использовать двоеточие в математике?
- 1.8.0.3 Как правильно читать выражение с двоеточием в математике?
- 1.8.0.4 Какие примеры использования двоеточия в математике вы можете привести?
- 1.8.0.5 Можете ли вы объяснить более подробно значение двоеточия в математике?
- 1.9 Использование двоеточия в вероятности и статистике
- 1.10 Примеры использования двоеточия в математике
Узнайте, что означает двоеточие в математике и как оно используется для обозначения различных математических понятий и операций. Подробное объяснение и примеры использования двоеточия в математике.
Двоеточие, это один из самых используемых символов в математике. Оно имеет несколько важных значений и широко используется для обозначения различных математических концепций и операций.
Во-первых, двоеточие в математике может использоваться для обозначения отношения между двумя величинами. Например, если у нас есть уравнение «x:y = 3:4», это означает, что отношение между x и y равно 3:4. Это может быть использовано для сравнения двух величин или для определения пропорции.
Во-вторых, двоеточие может использоваться для обозначения диапазона значений. Например, «x : 1 ≤ x ≤ 10» означает, что x принимает значения от 1 до 10 включительно. Это может быть полезно при описании интервалов или множеств.
Кроме того, двоеточие может использоваться для обозначения условия или определения. Например, «x : x > 0» означает, что x является положительным числом. Это может быть использовано для ограничения диапазона значений переменной или для задания определенных условий, которым должна удовлетворять величина.
Определение двоеточия в математике
В математике двоеточие обычно используется для обозначения разных понятий и операций. Оно может иметь несколько значений в зависимости от контекста.
Одним из основных значений двоеточия в математике является обозначение отношения. Например, запись «a:b» означает отношение «a к b». Такое отношение может иметь различные интерпретации в разных областях математики. Например, в теории вероятностей «a:b» может обозначать отношение вероятности события «a» к вероятности события «b». В геометрии двоеточие может использоваться для обозначения отношения между двумя точками или векторами.
Двоеточие также может использоваться для обозначения интервалов. Например, запись «a:b» означает интервал от значения «a» до значения «b». Этот интервал может быть открытым, закрытым или полуоткрытым в зависимости от контекста. Например, запись «(a:b)» означает открытый интервал, включающий все значения между «a» и «b», но не включая сами «a» и «b».
Двоеточие также может использоваться для обозначения диапазона значений. Например, запись «a:b» может означать все значения между «a» и «b», включая их самих. Это часто используется при задании диапазона индексов или при обозначении последовательностей чисел.
Использование двоеточия для обозначения отношений
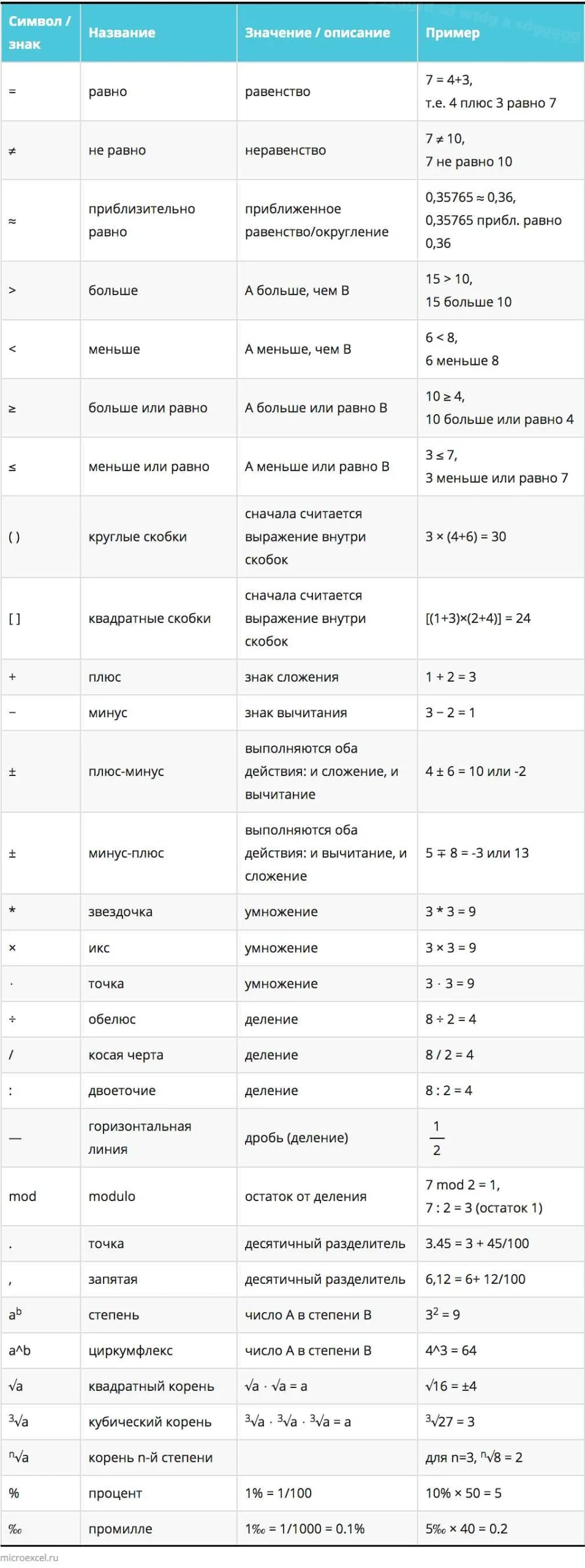
В математике двоеточие может использоваться для обозначения отношений между двумя элементами. Отношение может выражать различные связи между этими элементами, такие как равенство, неравенство, принадлежность и многое другое.
Например, двоеточие может использоваться для обозначения равенства между двумя числами. Например, если у нас есть уравнение 2x + 3y = 7, то мы можем записать его в виде 2x + 3y : 7, чтобы указать, что левая часть равна правой части.
Кроме того, двоеточие может использоваться для обозначения неравенства. Например, если мы хотим записать неравенство «x больше 5», мы можем записать его как x :> 5. Здесь двоеточие указывает на направление неравенства.
Двоеточие также может использоваться для обозначения принадлежности элемента к множеству. Например, если мы хотим записать, что число 2 принадлежит множеству натуральных чисел, мы можем записать это как 2 :∈ N. Здесь двоеточие указывает на принадлежность элемента к множеству.
В общем, двоеточие в математике используется для обозначения различных отношений между элементами. Правильное использование двоеточия позволяет ясно и точно выразить эти отношения и помогает в понимании математических выражений и уравнений.
Использование двоеточия в графиках и таблицах

В графиках и таблицах двоеточие также имеет свое значение и используется для разделения данных и их описания, а также для обозначения диапазона значений.
В графиках, ось времени часто обозначается числами, разделенными двоеточием. Например, на оси времени может быть отмечено 0:00, 1:00, 2:00 и так далее, обозначающие часы.
В таблицах двоеточие может использоваться для разделения заголовков столбцов и строк. Например, в таблице с расписанием занятий может быть использовано двоеточие для разделения дней недели и времени занятий.
Также, двоеточие может использоваться для обозначения диапазона значений. Например, в таблице с диапазоном температур может быть использовано двоеточие для обозначения диапазона от минимальной до максимальной температуры.
Пример использования двоеточия в графиках и таблицах:
- График с температурой за день: ось времени обозначена числами, разделенными двоеточием (0:00, 1:00, 2:00 и т.д.).
- Таблица с расписанием занятий: двоеточие используется для разделения дней недели и времени занятий (понедельник: 9:00-10:00, вторник: 10:00-11:00 и т.д.).
- Таблица с диапазоном температур: двоеточие используется для обозначения диапазона от минимальной до максимальной температуры (10°C:15°C, 15°C:20°C и т.д.).
Использование двоеточия в пропорциях и долях

Пропорция обычно записывается в следующем виде:
- a : b = c : d
Здесь a и b являются пропорциональными частями, а c и d – другими пропорциональными частями. В этой записи двоеточие означает «как» или «так как».
Доля, выраженная в процентах, записывается с использованием двоеточия:
- 20% : 80% = 1 : 4
Здесь процентное значение доли разделено двоеточием и указано в виде десятичной дроби. В этом случае двоеточие указывает на соответствие между процентами и десятичными долями.
Также двоеточие может быть использовано для обозначения долей в виде десятичных дробей:
- 1 : 2 : 3
Здесь двоеточие разделяет доли, где первая доля равна 1, вторая равна 2, а третья равна 3.
Использование двоеточия в пропорциях и долях является важным инструментом для анализа отношений и расчета долей в различных математических задачах.
Использование двоеточия в выражении условий
В математике двоеточие используется для обозначения условия, которое выполняется для данной переменной или выражения. Оно часто применяется в определении множества или функции, чтобы указать ограничения на значения переменных.
Например, при определении множества можно использовать двоеточие для указания условия, которое должно быть выполнено для элементов этого множества. Если A — множество всех натуральных чисел, то выражение A = {x : x > 0} означает, что множество A состоит из всех чисел x, которые больше нуля.
Двоеточие также используется в математических функциях для указания условия, при котором функция имеет определенное значение. Например, функция f(x) = x^2 : x > 0 означает, что значение функции f(x) равно квадрату числа x только в том случае, если x больше нуля.
Использование двоеточия в выражении условий позволяет более точно определить диапазон значений переменных или условия, при которых выражение или функция имеют смысл.
Использование двоеточия в функциях и формулах
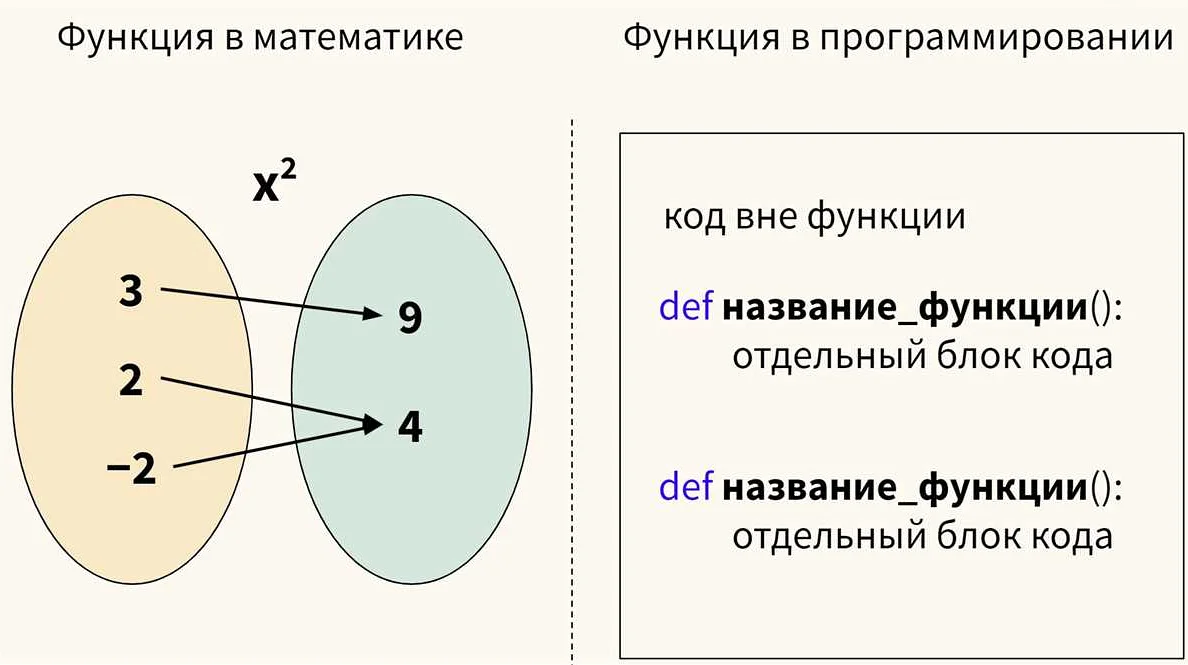
В математике двоеточие может использоваться для обозначения определения функций и записи формул.
Для обозначения функции двоеточие используется после имени функции и перед ее определением. Например, функция f(x) может быть определена следующим образом:
f(x) : x^2 + 1
В данном случае двоеточие показывает, что функция f(x) определена как выражение x^2 + 1.
Также двоеточие может использоваться для записи формул. Например, чтобы записать формулу для вычисления площади прямоугольника, можно использовать следующее выражение:
S : a * b
В данном случае двоеточие показывает, что выражение «a * b» является формулой для вычисления площади прямоугольника.
Использование двоеточия в функциях и формулах помогает уточнить и сделать более четкими определения и записи математических выражений.
Видео по теме:
Вопрос-ответ:
Какое значение имеет двоеточие в математике?
В математике двоеточие используется для обозначения отношений, условий или определений.
Как можно использовать двоеточие в математике?
Двоеточие можно использовать для обозначения отношений между двумя переменными, например, x:y. Также оно может использоваться для задания условий, например, x > 0 : x^2 > 0. И наконец, двоеточие может использоваться для определения новых понятий, например, множество всех четных чисел можно обозначить как {x : x является четным числом}.
Как правильно читать выражение с двоеточием в математике?
Выражение с двоеточием читается как «такой, что» или «такие, что». Например, x > 0 : x^2 > 0 читается как «x больше нуля такой, что x в квадрате больше нуля».
Какие примеры использования двоеточия в математике вы можете привести?
Примеры использования двоеточия в математике: x:y, где x и y — переменные, обозначает отношение между x и y; x > 0 : x^2 > 0, где x > 0 — условие, означает, что x должно быть больше нуля для того, чтобы x в квадрате было больше нуля; {x : x является четным числом}, где x является четным числом — определение множества всех четных чисел.
Можете ли вы объяснить более подробно значение двоеточия в математике?
Двоеточие в математике имеет несколько значений. Оно может использоваться для обозначения отношений между двумя переменными, например, x:y означает, что x относится к y. Также двоеточие может использоваться для задания условий, например, x > 0 : x^2 > 0 означает, что x должно быть больше нуля для того, чтобы x в квадрате было больше нуля. И наконец, двоеточие может использоваться для определения новых понятий, например, множество всех четных чисел можно обозначить как {x : x является четным числом}. Таким образом, двоеточие в математике употребляется для выражения отношений, условий и определений.
Использование двоеточия в вероятности и статистике

Двоеточие в математике имеет различные значения и применяется в различных областях, включая вероятность и статистику. В этих областях двоеточие используется для обозначения определенных понятий и отношений.
В вероятности двоеточие обычно используется для обозначения условной вероятности. Условная вероятность — это вероятность события A при условии, что произошло событие B, и обозначается как P(A|B). Двоеточие здесь разделяет событие A и условие B, и указывает на зависимость между ними.
Например, если мы хотим найти вероятность того, что человек выберет красный шар из корзины с красными и синими шарами, при условии, что он уже выбрал шар из этой корзины и он оказался красным, мы можем записать это как P(красный|выбран красный).
В статистике двоеточие может использоваться для обозначения параметров и оценок. Например, в линейной регрессии двоеточие может разделять регрессоры (независимые переменные) и параметры модели (коэффициенты), и записывается как y = b0 + b1x1 + b2x2 + … + bnxn, где bi — параметры модели, xi — регрессоры.
Двоеточие также может использоваться для обозначения отношений и равенств в статистике. Например, если мы хотим указать, что две случайные величины X и Y независимы, мы можем записать это как X ⊥ Y, где ⊥ обозначает независимость между X и Y.
Использование двоеточия в вероятности и статистике позволяет нам точно и ясно выразить отношения и понятия в этих областях, что способствует более точному и понятному анализу данных и выводу статистических закономерностей.
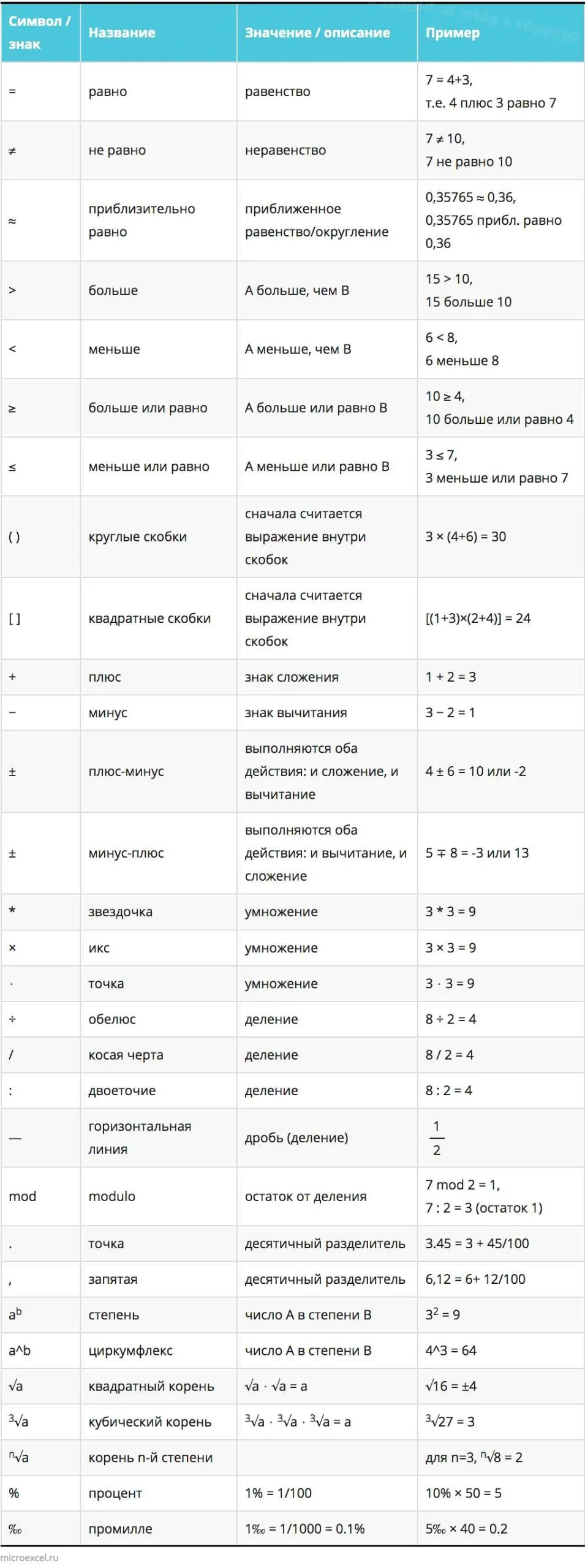
Примеры использования двоеточия в математике
Двоеточие в математике может использоваться для обозначения различных математических отношений и операций. Вот некоторые примеры:
- Двоеточие в записи множества: множество A может быть записано как A = {x : x > 0}, что означает, что A состоит из всех элементов x, для которых x больше нуля.
- Двоеточие в записи условия: в математических уравнениях и неравенствах двоеточие может использоваться для обозначения условия. Например, уравнение x + 2 = 5 может быть записано как x : x + 2 = 5, что означает, что значение x удовлетворяет условию x + 2 = 5.
- Двоеточие в записи вероятности: в теории вероятностей двоеточие может использоваться для обозначения условной вероятности. Например, P(A : B) обозначает вероятность события A при условии, что событие B произошло.
- Двоеточие в записи пропорции: двоеточие может использоваться для обозначения пропорции или отношения между двумя значениями. Например, a : b обозначает пропорцию между значениями a и b, где a является числителем, а b — знаменателем.
Это лишь несколько примеров использования двоеточия в математике. Оно широко применяется для обозначения различных математических концепций и отношений.



Статья очень понравилась! Как школьник, я всегда задавался вопросом о значении двоеточия в математике. Спасибо автору за подробное объяснение и примеры использования! Теперь я лучше понимаю, что двоеточие используется для обозначения различных математических отношений, таких как соответствие, делимость и пропорциональность. Это очень полезно для решения задач и упрощения записи математических выражений. Например, я теперь знаю, что запись «a:b» означает, что a и b соответствуют друг другу или что a делится на b без остатка. Это помогает мне лучше интерпретировать математические выражения и решать задачи более эффективно. Благодаря статье я чувствую себя более уверенно в изучении математики. Советую всем ознакомиться с этой статьей, чтобы лучше понять значение двоеточия в математике!
Двоеточие в математике – это один из важных знаков пунктуации, который играет значительную роль в обозначении различных математических выражений и отношений. Во-первых, двоеточие может использоваться для обозначения отношения между двумя величинами. Например, в записи «a:b» оно указывает на отношение числа a к числу b. Это помогает нам сравнивать и анализировать числа и их соотношения. Кроме того, двоеточие может быть использовано для обозначения диапазона значений. Например, запись «x:y» указывает на все числа между x и y, включая их самих. Такой подход часто используется при задании диапазона переменных или интервалов. Также двоеточие может использоваться при обозначении условия или ограничения. Например, запись «x:y | x > 0» означает, что значение переменной x должно быть больше нуля. И наконец, двоеточие может использоваться в математических формулах для обозначения различных операций и отношений. Например, в записи «f(x) : g(x)» оно указывает на отношение функций f и g. Таким образом, двоеточие в математике имеет множество значений и применений, которые помогают нам более точно и ясно выражать математические идеи и отношения.
Двоеточие в математике – это знак препинания, который имеет свою особую значимость. Оно используется для обозначения отношения между двумя величинами или для введения определений и обозначений. Одним из примеров использования двоеточия является его применение при задании диапазона значений. Например, если мы хотим указать, что переменная «х» принимает значения от 1 до 10, мы можем записать это следующим образом: «х: 1 ≤ х ≤ 10». Двоеточие здесь указывает на связь между переменной «х» и заданным диапазоном значений. Другой пример использования двоеточия – это введение определений и обозначений. Например, если мы хотим определить, что «а» является квадратом числа «b», мы можем записать это так: «а: а = b^2». Здесь двоеточие указывает на то, что «а» определяется как квадрат числа «b». Двоеточие также используется при записи соотношений и уравнений. Например, если мы хотим записать уравнение прямой, проходящей через точку (1, 2) и параллельной оси OX, мы можем записать его так: «у: у = 2». Здесь двоеточие указывает на уравнение прямой. Таким образом, значение двоеточия в математике заключается в указании отношений между математическими объектами, введении определений и обозначений, а также в записи уравнений и соотношений. Этот знак препинания играет важную роль в математической нотации, облегчая понимание и запись различных математических концепций и идей.
Двоеточие в математике – это важный символ, который используется для разделения чисел или выражений. Оно помогает нам создавать логическую связь между различными элементами в уравнениях и формулах. Например, двоеточие может быть использовано для обозначения интервала. Например, [1:5] означает, что мы берем все числа включительно от 1 до 5. Это полезно, когда нам нужно указать диапазон значений или ограничить множество чисел. Двоеточие также используется в отображениях и функциях. Например, f(x): x^2 означает, что функция f принимает значение x и возвращает значение x^2. Это позволяет нам определить математические отношения и связи между переменными. Кроме того, двоеточие может быть использовано для обозначения соотношений или условий. Например, x:y означает, что x и y связаны некоторым отношением или соотношением. Это помогает нам формализовать и описывать математические отношения и законы. В целом, двоеточие в математике является мощным средством для создания логических связей и определения отношений между различными элементами. Оно помогает нам более точно и ясно формулировать и решать математические задачи.