Что значит прямые скобки в математике

Прямые скобки в математике используются для обозначения группировки выражений и операций. Узнайте, как использовать прямые скобки в математических формулах и выражениях для повышения их ясности и удобочитаемости.

В математике прямые скобки [ ] являются одним из наиболее часто используемых математических символов. Они выполняют несколько важных функций, и понимание их значения является неотъемлемой частью математической грамотности. В этой статье мы разберемся, как применяются прямые скобки в математике и приведем несколько примеров их использования.

Одним из основных применений прямых скобок в математике является обозначение интервалов. Интервал – это упорядоченное множество чисел, которые находятся между двумя границами. В таких случаях прямые скобки используются для обозначения нестрогих границ интервала. Например, интервал [1, 5] обозначает все числа, которые находятся между 1 и 5 включительно, в то время как интервал (1, 5) обозначает все числа, которые находятся между 1 и 5, но не включая сами границы.

Прямые скобки также используются для обозначения массивов или списка элементов. В программировании они используются для создания и обращения к элементам массива. Например, [1, 2, 3] обозначает массив из трех элементов: 1, 2 и 3.

Прямые скобки могут также использоваться для обозначения матриц и векторов. Например, [1 2 3] может обозначать вектор-строку из трех элементов, а [1; 2; 3] – вектор-столбец. В матрицах прямые скобки используются для разделения строк или столбцов.

В конечном счете, понимание значения прямых скобок в математике позволяет нам более точно описывать и анализировать различные математические концепции и явления. Они есть везде, от алгебры до программирования, и являются важным инструментом в нашем математическом арсенале.

Использование прямых скобок в математике: основные моменты и примеры

Прямые скобки [ ] в математике имеют несколько различных значений и применяются в различных контекстах. Вот основные моменты и примеры использования прямых скобок:

1. Обозначение интервалов:

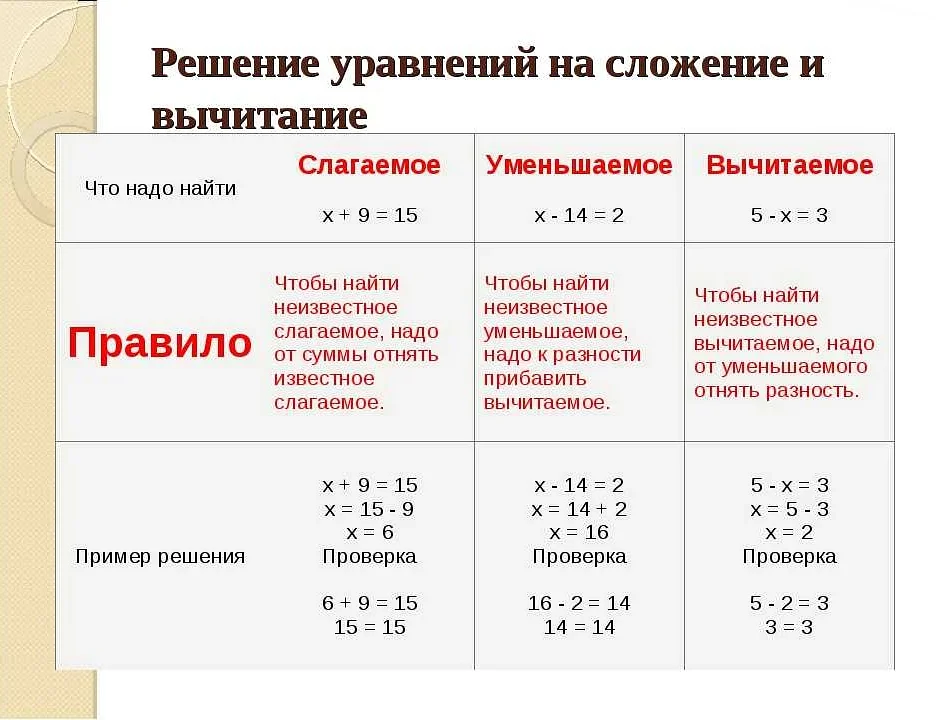
Прямые скобки используются для обозначения интервалов на числовой прямой. Например, [a, b] обозначает закрытый интервал от a до b, включая граничные значения a и b. Другой пример — [a, b) обозначает полузакрытый интервал от a до b, включая a, но исключая b.

2. Индексация и обозначение массивов:

В математике прямые скобки также используются для индексации элементов в массивах или векторах. Например, A[1] обозначает первый элемент массива A.

3. Матричные операции:

В матричных операциях прямые скобки используются для обозначения матрицы или массива элементов. Например, A = [aij] обозначает матрицу A с элементами aij.

4. Обозначение условий и функций:

Прямые скобки могут использоваться для обозначения условий или функций. Например, [x] может обозначать функцию «дробная часть числа x», возвращающую целую часть числа x.

Примеры:

1. Интервал [0, 1] обозначает все числа от 0 до 1, включая 0 и 1.

2. A[2] обозначает второй элемент массива A.

3. Матрица A = [aij] имеет элементы aij.

4. [x] обозначает дробную часть числа x.

Все эти примеры являются лишь небольшой частью того, как прямые скобки могут использоваться в математике. Важно понимать контекст использования и правила, чтобы правильно интерпретировать и использовать прямые скобки в математических выражениях.

Определение и назначение прямых скобок

Прямые скобки выполняют несколько функций:

1. Группировка: Прямые скобки используются для группировки элементов, чтобы указать, что операции внутри скобок должны быть выполнены в первую очередь. Это помогает установить правильный порядок вычислений.
2. Обозначение интервала: Прямые скобки могут быть использованы для обозначения интервала чисел. Например, [1, 5] обозначает все числа от 1 до 5 включительно.
3. Обозначение матриц и векторов: В линейной алгебре прямые скобки используются для обозначения матриц и векторов. Матрица или вектор заключается в прямые скобки, а элементы разделяются запятыми.

Например, выражение [2 + (3 — 1)] * 4 означает, что сначала нужно выполнить операцию внутри скобок (3 — 1), затем сложить результат с 2 и, наконец, умножить полученную сумму на 4.

Прямые скобки — важный элемент математических выражений, которые помогают определить порядок выполнения операций и четко обозначить интервалы чисел, матрицы и векторы. Использование прямых скобок позволяет упростить и структурировать математические выражения, что облегчает их понимание и вычисление.

Примеры прямых скобок

Прямые скобки в математике используются для обозначения различных операций и выражений. Ниже приведены несколько примеров их использования:

1. Скобки для обозначения векторов: [a, b, c]. Векторы могут быть использованы для представления направления, силы или координат в пространстве. Например, [2, 4, 6] обозначает вектор с координатами (2, 4, 6).

2. Скобки для обозначения матриц: [A, B, C]. Матрицы используются для представления линейных преобразований и систем уравнений. Например, [1, 2, 3; 4, 5, 6] обозначает матрицу размером 2×3 с элементами (1, 2, 3) и (4, 5, 6).

3. Скобки для обозначения интервалов: [a, b]. Интервалы используются для задания непрерывных значений или диапазонов. Например, [1, 5] обозначает интервал от 1 до 5 включительно.

4. Скобки для обозначения функций: f(x). Функции могут принимать аргументы (x) и возвращать результаты. Например, f(x) = x^2 обозначает функцию, которая возвращает квадрат аргумента.

5. Скобки для обозначения подмножеств: {x | x > 0}. Подмножества используются для задания условий или ограничений на множества. Например, {x | x > 0} обозначает множество всех чисел x, которые больше нуля.

Это лишь несколько примеров использования прямых скобок в математике. Они являются важным инструментом для обозначения различных операций и выражений.

Использование прямых скобок в алгебре

В алгебре прямые скобки часто используются для обозначения группировки выражений и задания порядка операций. Они позволяют установить приоритет выполнения операций, определяя, какие операции должны быть выполнены первыми.

Прямые скобки могут быть использованы для выделения и группировки частей выражения. Например, выражение (2 + 3) * 4 означает, что сначала нужно сложить числа 2 и 3, а затем полученную сумму умножить на 4. Если бы скобок не было, операции выполнялись бы в порядке, определенном приоритетом операций, и результат был бы другим: 2 + 3 * 4 = 2 + 12 = 14.

Прямые скобки также используются для указания аргументов функций. Например, в выражении sin(30°) скобки указывают, что функция синуса принимает аргументом угол 30°.

Прямые скобки в алгебре позволяют более ясно и однозначно определить порядок операций и группировку выражений. Их правильное использование способствует правильному решению математических задач и избеганию ошибок.

Использование прямых скобок в геометрии

Прямые скобки также имеют важное значение в геометрии. В данном контексте они используются для обозначения отрезков, отрезков прямых, векторов и углов.

Одна из основных функций прямых скобок в геометрии — обозначение отрезков. Например, отрезок AB можно обозначить как [AB]. Это помогает четко указать начало и конец отрезка.

Также прямые скобки используются для обозначения отрезков прямых. Например, если AB — отрезок прямой, то его можно обозначить как [AB]. Это позволяет отличить отрезок от точки на прямой, которая обозначается без скобок.

Кроме того, прямые скобки могут использоваться для обозначения векторов. Например, если A — начальная точка, а B — конечная точка вектора, то вектор AB обозначается как [AB]. Это помогает указать направление и длину вектора.

Наконец, прямые скобки могут быть использованы для обозначения углов. Например, угол ABC можно обозначить как (ABC). Это помогает распознать угол и отличить его от точки на прямой или отрезка прямой.

Использование прямых скобок в геометрии помогает установить четкие обозначения для отрезков, отрезков прямых, векторов и углов. Это делает геометрические выкладки более понятными и удобными для работы.

Прямые скобки в теории множеств

Прямые скобки, также известные как квадратные скобки, имеют особое значение в теории множеств. Они используются для обозначения множества элементов или для указания свойств или условий, которым должны удовлетворять элементы множества.

Прямые скобки могут быть использованы для описания множеств, например:

{1, 2, 3} — это множество, содержащее элементы 1, 2 и 3.

{x | x < 5} — это множество всех элементов x, которые меньше 5.

Прямые скобки могут также использоваться для указания свойств или условий, например:

{x ∈ R | x > 0} — это множество всех элементов x из множества действительных чисел, которые больше нуля.

{x | x^2 = 4} — это множество всех элементов x, для которых квадрат x равен 4.

Прямые скобки в теории множеств используются для создания и описания множеств, а также для указания свойств или условий, которым должны удовлетворять элементы множества.

Прямые скобки в тригонометрии

Прямые скобки в тригонометрии используются для обозначения аргумента тригонометрических функций, таких как синус, косинус и тангенс.

Например, запись sin(x) обозначает синус угла x, а запись cos(x) обозначает косинус угла x.

Аргумент функций в тригонометрии может быть выражен в радианах или градусах. Если аргумент выражен в радианах, то прямые скобки обычно не используются.

Например, для вычисления синуса угла в радианах, можно написать sin(x), где x — значение угла в радианах.

Однако если аргумент выражен в градусах, то прямые скобки могут использоваться для явного указания, что аргумент является углом.

Например, для вычисления синуса угла в градусах, можно написать sin[∠x], где ∠x — значение угла в градусах.

Использование прямых скобок в тригонометрии позволяет ясно указать, что аргумент функции — это угол, и облегчает понимание записи тригонометрических выражений.

Прямые скобки в математическом анализе

В математическом анализе прямые скобки [, ] играют важную роль и используются для обозначения различных математических объектов.

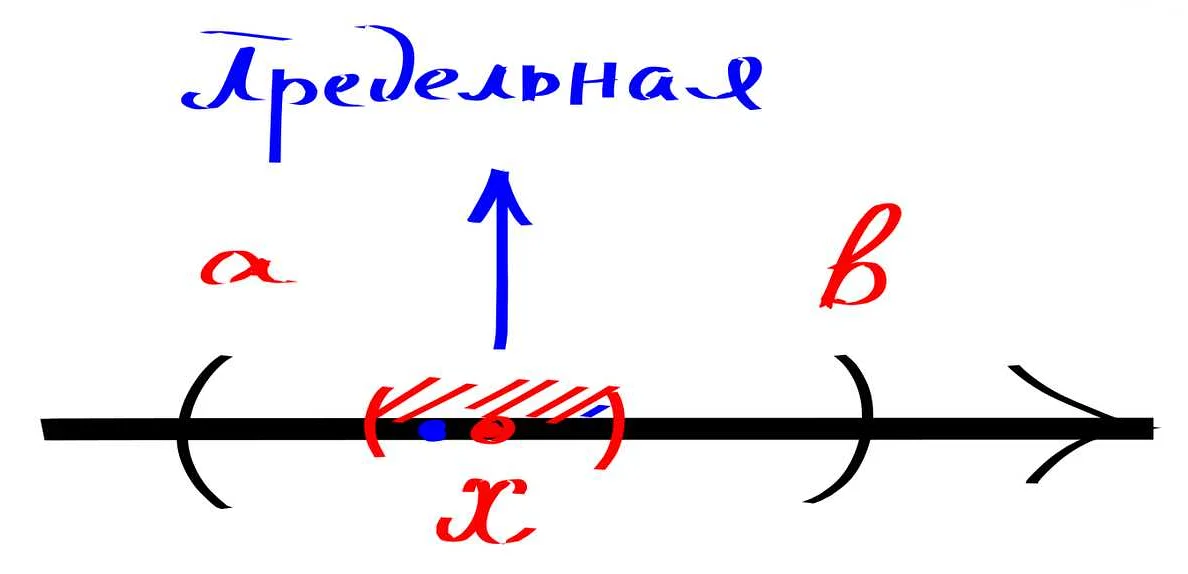
Одним из основных применений прямых скобок является обозначение отрезков на числовой прямой. Если a и b — две точки на числовой прямой, то отрезок [a, b] представляет собой множество всех точек, лежащих между точками a и b, включая сами эти точки. Например, отрезок [2, 5] включает в себя все числа от 2 до 5, включая как 2, так и 5.

Кроме того, прямые скобки используются для обозначения замкнутых интервалов. Интервал [a, b] включает в себя все числа от a до b, включая как a, так и b. Например, интервал [0, 1] включает в себя все числа от 0 до 1, включая как 0, так и 1.

Прямые скобки также могут использоваться для обозначения области определения функций. Например, если f(x) — функция, то областью определения этой функции может быть отрезок [a, b]. Это означает, что функция f(x) определена для всех значений x, лежащих на отрезке [a, b].

Кроме указанных примеров, прямые скобки могут использоваться и в других математических контекстах для обозначения различных объектов и операций.

Вопрос-ответ:

Зачем нужны прямые скобки в математике?

Прямые скобки в математике используются для обозначения группировки выражений и задания приоритета операций. Они позволяют указать, какие операции должны быть выполнены в первую очередь. Прямые скобки также используются для обозначения интервалов и множеств.

Какие операции имеют больший приоритет — прямые скобки или скобки второго уровня?

Прямые скобки имеют наивысший приоритет, и операции внутри них выполняются первыми. Если внутри прямых скобок находятся другие скобки, то сначала выполняются операции внутри этих вложенных скобок, а затем уже операции внутри внешних прямых скобок.

Какие примеры можно привести для объяснения использования прямых скобок в математике?

Примером использования прямых скобок может служить следующее выражение: 2 * (3 + 4). Здесь прямые скобки указывают, что нужно сначала выполнить операцию сложения внутри скобок, а затем уже умножение результата на число 2. Также прямые скобки могут использоваться для обозначения интервалов, например, [1, 5] — это интервал от числа 1 до числа 5 включительно.

Какие еще применения могут быть у прямых скобок в математике?

Прямые скобки могут использоваться для обозначения множеств. Например, {1, 2, 3} — это множество из чисел 1, 2 и 3. Также прямые скобки могут использоваться для обозначения матриц, векторов и других структур данных. В общем случае, прямые скобки позволяют группировать элементы и задавать структуру данных.

Можно ли использовать прямые скобки вместо скобок второго уровня и наоборот?

В общем случае, нельзя использовать прямые скобки вместо скобок второго уровня и наоборот. Однако, в некоторых случаях, когда в выражении имеется только один уровень вложенности, прямые скобки могут заменяться на скобки второго уровня и наоборот. Например, (1 + 2) можно записать как [1 + 2] и наоборот.

Видео по теме: