Что означает символ e в математике

Символ e в математике обозначает основание натурального логарифма. Узнайте, как использовать и понять значение этого важного математического символа.

Символ e в математике имеет особое значение и широкое применение. Он является одной из констант, которые встречаются в различных математических формулах и уравнениях. Этот символ был введен Леонардом Эйлером в XVIII веке и получил название в честь его фамилии. Он обладает рядом уникальных свойств и используется в различных областях математики.

Значение символа e равно приблизительно 2.71828. Он является основанием натурального логарифма и является решением уравнения e^x = 1. Это означает, что e возведенная в любую степень x всегда равна единице. Это свойство делает его очень полезным в решении различных задач и уравнений в математике, физике и других науках.

Символ e также используется в комплексном анализе, где он играет важную роль в формуле Эйлера, связывающей комплексные числа, функции и тригонометрию. Эта формула имеет вид e^(iπ) + 1 = 0 и является одной из самых известных формул в математике.

В математическом анализе символ e используется для определения производной. Производная функции f(x) в точке x равна пределу (приближению) отношения приращения функции к приращению ее аргумента при бесконечном стремлении приращения аргумента к нулю. При этом именно значение символа e играет ключевую роль в этом определении и позволяет вычислять производные функций на основе этого понятия.

В заключение, символ e в математике имеет глубокое значение и широкое применение. Он обладает уникальными свойствами и используется в различных областях науки и техники. Понимание его значения и свойств позволяет решать сложные задачи и уравнения, а также понять многие фундаментальные концепции в математике.

Что такое символ e в математике

Символ e был впервые введен и использован Леонардом Эйлером в XVIII веке. Он назвал его в честь нидерландского математика Иоганна Бернулли, который использовал букву e для обозначения базы экспоненциальной функции.

Основная особенность символа e заключается в его связи с экспоненциальной функцией. Экспоненциальная функция с основанием e имеет следующий вид: f(x) = e^x. Она имеет множество применений в различных областях математики и наук, таких как физика, экономика, биология и т.д.

Символ e также является ключевым элементом в формуле для расчета процентного прироста при непрерывном росте или убывании. Формула имеет вид: A = P * e^(rt), где A — конечная сумма, P — начальная сумма, r — процентная ставка, t — время.

Символ e также встречается в формуле для вычисления производной экспоненциальной функции: f'(x) = e^x. Эта формула является одной из основных формул дифференциального исчисления.

В заключение, символ e в математике играет важную роль и имеет множество применений в различных областях. Он является ключевым элементом экспоненциальных функций и используется для расчетов процентного прироста, а также в дифференциальном исчислении.

Значение символа e в естественном логарифме

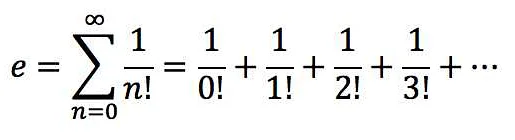
Символ e в математике представляет собой особое число, называемое числом Эйлера или основанием натурального логарифма. Это число приближенно равно 2,71828. Число e возникает в различных областях математики и физики.

В естественном логарифме, который обозначается как ln(x), число e играет ключевую роль. Естественный логарифм определяется как обратная функция к экспоненте. То есть, если y = e^x, то ln(y) = x. Это взаимосвязь между экспонентой и естественным логарифмом является основой многих математических и физических моделей.

Важным свойством числа e в естественном логарифме является то, что его производная при равной аргументе равна самому числу e. То есть, если f(x) = e^x, то f'(x) = e^x. Это свойство делает число e важным для решения различных задач дифференциального и интегрального исчислений.

Число e также используется в формуле для вычисления непрерывного процента с учетом сложного процента. Формула имеет вид A = P(1 + r/n)^(nt), где A — конечная сумма, P — начальный капитал, r — процентная ставка, n — количество периодов в году, t — общее количество лет. Число e в этой формуле использовано для представления непрерывного процента, когда количество периодов стремится к бесконечности.

В заключение, число e в естественном логарифме является важным математическим константой, которая играет роль основания натурального логарифма и находит широкое применение в различных областях математики и физики.

Свойства символа e в математике

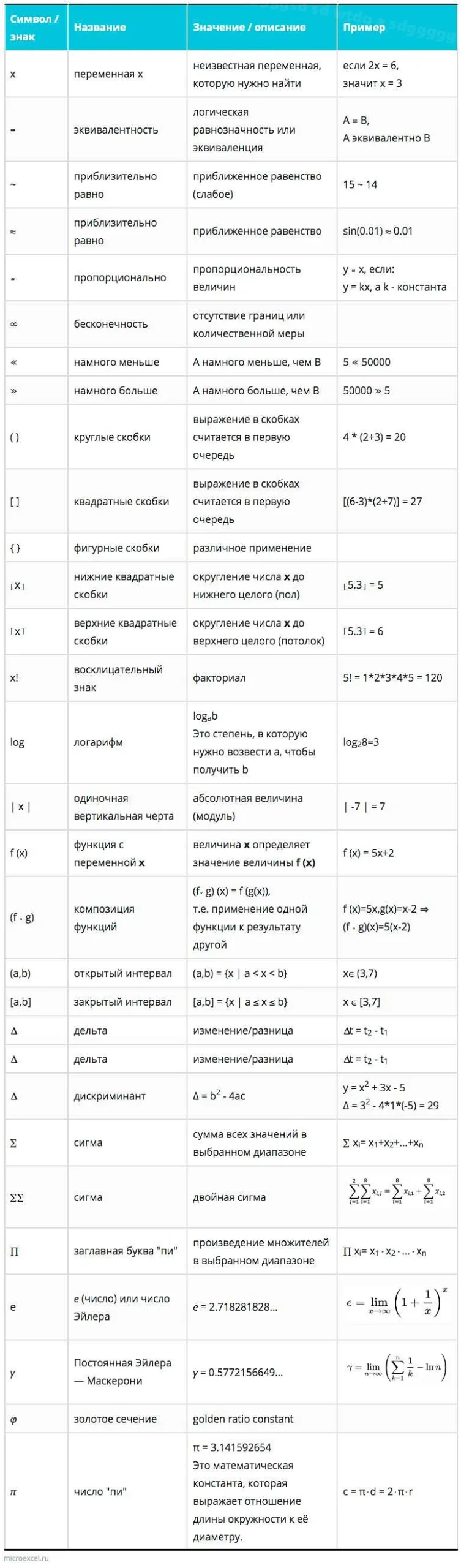
1. Натуральный логарифм: Символ e используется для определения натурального логарифма и его основных свойств. Натуральный логарифм описывает рост или убывание некоторых явлений, таких как популяция, температура или финансовые инвестиции.
2. Экспонента: Символ e также используется для определения экспоненты, которая представляет собой функцию, обратную к натуральному логарифму. Экспонента e^x описывает рост или убывание явления в экспоненциальной шкале.
3. Ряд Тейлора: Символ e встречается в разложении функций в ряд Тейлора. Ряд Тейлора позволяет аппроксимировать сложные функции с помощью более простых функций, основанных на значениях символа e.
4. Дифференцирование и интегрирование: Символ e играет важную роль в дифференцировании и интегрировании функций. Например, производная функции e^x равна самой функции, а интеграл от функции e^x также связан с символом e.
5. Математические константы: Символ e является одной из основных математических констант, вместе с числами π и i. Они встречаются во множестве математических формул и имеют свои уникальные свойства и применение.

Эти свойства символа e делают его незаменимым инструментом в математике и науке. Он используется для моделирования и анализа множества явлений, а также для разработки математических моделей и решения сложных задач.

Применение символа e в экономике

К примеру, формула для непрерывного процента может быть записана как:

A = P*e^(rt)

где:

• A – конечная сумма;
• P – начальная сумма;
• r – процентная ставка;
• t – время;
• e – число Эйлера.

Эта формула позволяет рассчитать будущую стоимость инвестиции или долгосрочную стоимость товара или услуги с учетом непрерывного роста.

Кроме того, число e используется в моделировании экономических процессов. Например, в моделировании роста населения или распределения доходов. Это число помогает рассчитать экспоненциальный рост или убывание в экономических моделях.

Таким образом, символ e играет важную роль в экономике и финансовой математике, позволяя ученным и экономистам рассчитывать будущие стоимости, моделировать экономические процессы и прогнозировать тенденции развития.

Применение символа e в физике

Кроме того, символ e широко используется для обозначения экспоненциальных функций и числа Эйлера. Число Эйлера (e) является математической константой, которая приблизительно равна 2,71828. Оно возникает в различных областях физики, включая статистическую механику, квантовую механику и теорию вероятностей. Число Эйлера также используется в формулах, описывающих рост и распад популяций, процессы диффузии и другие явления.

Другое применение символа e в физике связано с единицей измерения заряда элементарной частицы. Заряд элементарной частицы обычно измеряется в единицах элементарного заряда (e). Например, протон имеет положительный заряд, равный +1e, а античастица протона — антипротон — имеет заряд, равный -1e. Таким образом, использование символа e для обозначения заряда в физике позволяет удобно работать с элементарными зарядами и их комбинациями.

В заключение, символ e в физике имеет несколько значений и применений. Он используется для обозначения элементарного заряда, числа Эйлера и единицы измерения заряда элементарных частиц. Знание и понимание этих значений помогает физикам в изучении и описании различных явлений в мире физики.

Применение символа e в статистике

Экспоненциальное распределение широко применяется в статистике для моделирования времени между двумя последовательными событиями. Например, время между появлением двух звонков в центре колл-центра или время между отказами оборудования в производственной линии.

В экспоненциальном распределении параметр e используется для определения интенсивности событий. Интенсивность обозначает скорость, с которой события происходят в единицу времени. Чем больше значение параметра e, тем выше интенсивность событий.

При использовании экспоненциального распределения в статистике, символ e позволяет вычислить вероятность того, что время между двумя событиями будет меньше или больше определенного значения. Это позволяет статистикам исследовать и анализировать различные аспекты временных интервалов и прогнозировать вероятность наступления событий в будущем.

Таким образом, символ e играет важную роль в статистике, позволяя моделировать и анализировать временные интервалы между событиями и определять вероятность наступления событий в определенный период времени.

Применение символа e в инженерии

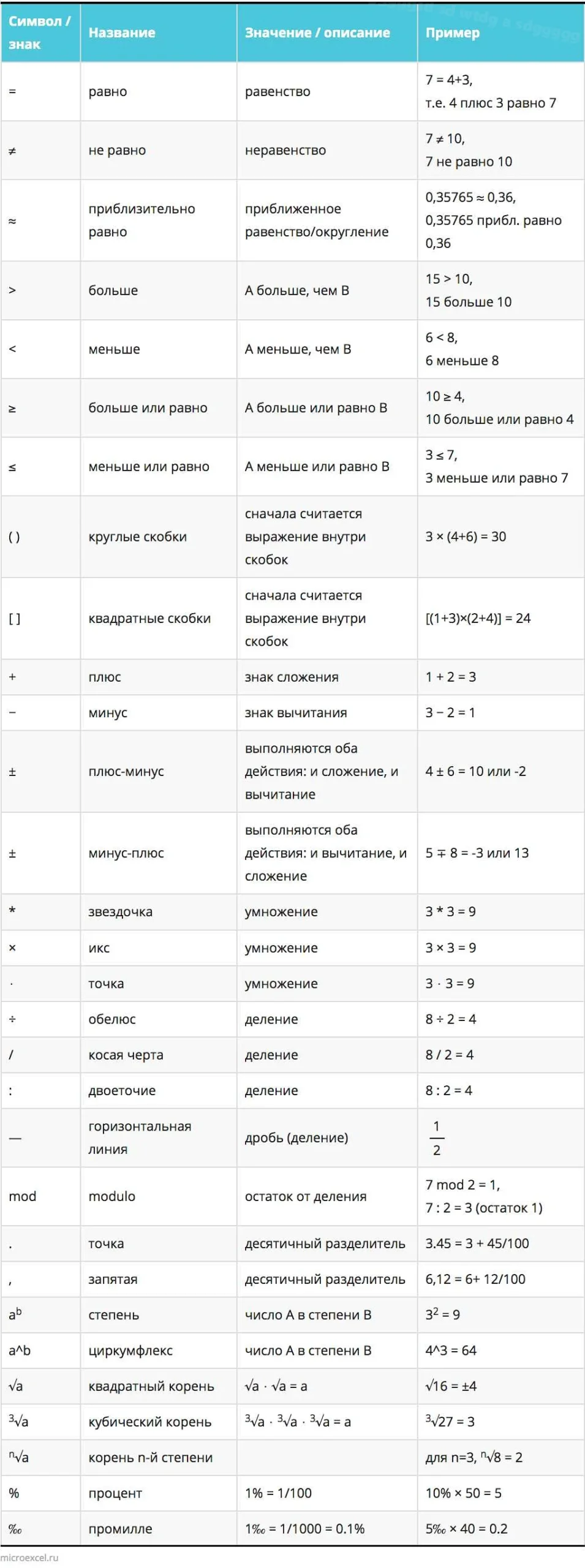
Символ e в инженерии имеет несколько применений. Одно из самых распространенных использований символа e связано с числом Эйлера.

Число Эйлера e – это одна из важнейших математических констант, которая используется в различных инженерных расчетах. Значение числа Эйлера приближено равно 2,71828. Оно является основой натурального логарифма и имеет множество применений в научных и инженерных расчетах.

Символ e также используется для обозначения экспоненты в инженерии. Экспоненциальная функция е^x широко применяется при моделировании и решении различных инженерных задач, таких как расчеты электрических цепей, теплопроводности, анализ статических и динамических систем и других.

Кроме того, символ e используется для обозначения ошибки приближенных вычислений в инженерии. Такая ошибка обычно обозначается как e_m и позволяет оценить точность и надежность результатов вычислений.

Таким образом, символ e в инженерии имеет важное значение и широко применяется при решении различных инженерных задач.

Применение символа e в компьютерных науках

Символ e, который имеет математическое значение, также играет важную роль в компьютерных науках. В программировании и информатике, e обычно обозначает основание натурального логарифма, которое приближается к 2.71828.

Понимание значения символа e в компьютерных науках позволяет разработчикам использовать его для различных вычислений и алгоритмов. Например, символ e может быть использован в вычислениях экспоненциальной функции, при решении дифференциальных уравнений, а также в области машинного обучения и искусственного интеллекта.

В компьютерных науках символ e также широко используется в области анализа алгоритмов и сложности вычислений. Он может быть использован для выражения временной сложности алгоритма, что позволяет оценить эффективность программы и выбрать оптимальное решение для выполнения задачи.

Таким образом, в компьютерных науках символ e играет важную роль и является неотъемлемой частью математических вычислений и алгоритмов. Понимание его значения помогает разработчикам создавать более эффективные и точные программы.

Вопрос-ответ:

Чему равен символ e в математике?

Символ e в математике представляет собой основание натурального логарифма и приближенно равен 2,71828.

Каким образом символ e применяется в математике?

Символ e используется в различных областях математики, таких как анализ, теория вероятности, дифференциальное и интегральное исчисление. Он играет важную роль в решении уравнений, моделировании естественных явлений и нахождении пределов.

Каково происхождение символа e в математике?

Символ e был предложен швейцарским математиком Леонардом Эйлером в 1731 году. Он использовал букву e в качестве обозначения основания натурального логарифма, которое ранее обозначалось как b.

Как символ e связан с экспоненциальной функцией?

Символ e является основанием экспоненциальной функции. Экспонента e^x определяется как предел (1 + 1/n)^n при n стремящемся к бесконечности. Эта экспоненциальная функция имеет много важных свойств и применений в математике и естественных науках.

Как символ e связан с процентами и сложными процентами?

Символ e используется в формуле для расчета сложных процентов. Формула A = P(1 + r/n)^(nt), где A — итоговая сумма, P — начальная сумма, r — годовая процентная ставка, n — количество раз, когда проценты начисляются за год, и t — количество лет. Если мы возьмем предел n стремящемся к бесконечности, то (1 + r/n)^n сойдется к значению e^r, и формула упростится до A = Pe^(rt).

Что означает символ e в математике?

Символ e в математике обозначает число Эйлера, которое примерно равно 2,71828. Это особое число, которое используется во многих математических формулах и имеет множество интересных свойств.

Какое значение имеет символ e в математике?

Символ e в математике имеет несколько значений. Во-первых, это число Эйлера, которое является основой натурального логарифма. Во-вторых, e используется в формулах для рассчета процентного прироста, а также в экспоненциальных функциях. Кроме того, число e встречается в ряде других математических приложениях, таких как теория вероятностей и финансовая математика.

Видео по теме: