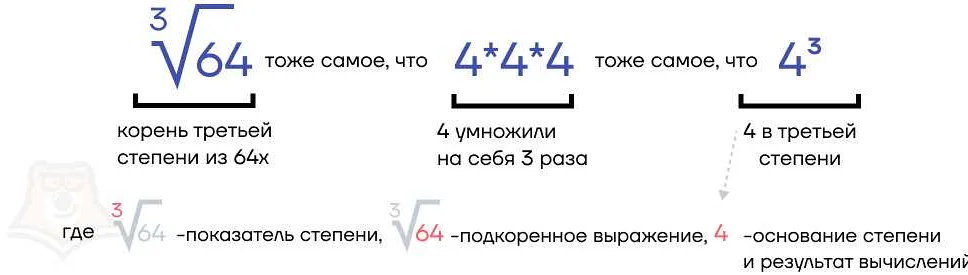
Что значит символ е в математике

Символ е в математике представляет собой основание натурального логарифма. Он играет важную роль в различных областях математики и науки, таких как анализ, статистика, теория вероятностей и многое другое. Узнайте, как символ е используется в различных математических формулах и почему он является одним из наиболее важных чисел в математике.

Символ «е» в математике играет важную роль и широко используется в различных математических областях. Этот символ обозначает одно из наиболее важных чисел в математике — число Эйлера или экспоненту.

Число Эйлера (e) является основанием натурального логарифма и имеет приближенное значение 2,71828. Оно появляется во многих математических формулах и уравнениях и имеет ряд уникальных свойств, которые делают его незаменимым инструментом в решении различных задач.

Символ «е» используется в экспоненциальных функциях, ряды Тейлора, вероятностных распределениях и других математических концепциях. Он позволяет описывать и предсказывать явления с использованием комплексных чисел и процентных изменений.

Экспонента с основанием «е» имеет множество интересных свойств и применений в науке и технике. Она позволяет моделировать рост и убывание в различных процессах, а также предсказывать будущие значения на основе текущих данных. Кроме того, число Эйлера используется в финансовых расчетах, статистике, физике, инженерии и других областях, где важно точное и эффективное описание и анализ данных.

Основные свойства символа «е» в математике

Основное свойство символа «е» — это его способность описывать экспоненциальный рост или убывание. Экспоненциальная функция с основанием «е» имеет особую особенность, что ее производная в любой точке равна самой функции в этой точке. Это свойство делает символ «е» незаменимым инструментом в моделировании естественных процессов, таких как рост популяции, распад радиоактивных веществ и других.

Символ «е» также имеет свои применения в решении уравнений и задачах, связанных с вероятностью и статистикой. Он является основой для экспоненциального распределения, которое широко используется для моделирования случайных событий с постоянной интенсивностью.

В заключение, символ «е» играет важную роль в математике, позволяя описывать и анализировать экспоненциальные процессы, моделировать случайные события и решать различные задачи, связанные с вероятностью и статистикой.

Естественное число «е»

Число «е» является основанием натурального логарифма и является решением такого уравнения: e^x=1, где x — неизвестное.

Свойства числа «е» могут быть использованы для решения различных задач, связанных с экспоненциальным ростом и изменением величин. Оно активно применяется в различных областях науки и инженерии, таких как физика, экономика, статистика, теория вероятностей и другие.

Число «е» также является иррациональным числом, то есть его десятичное представление бесконечно не периодическое и не может быть точно представлено конечной десятичной дробью.

Значение числа «е» можно приближенно вычислить с помощью различных методов и алгоритмов, таких как ряд Тейлора или использование компьютерных программ.

Естественное число «е» играет важную роль в математике и имеет множество применений, делая его одной из наиболее изучаемых и интересных констант в науке.

Математическая константа «е»

Константа «е» встречается во множестве математических теорем, формул и уравнений. Она играет особую роль в областях, связанных с экспоненциальным ростом и рассматривается в различных ветвях математики, таких как анализ, теория вероятностей, дифференциальные уравнения и других.

Важное свойство константы «е» заключается в том, что ее значение является основанием экспоненциальной функции. То есть, экспонента с основанием «е» описывает наиболее естественный способ роста или убывания во многих естественных и научных явлениях.

Константа «е» также тесно связана с комплексными числами и теорией функций. Она является основой для построения комплексной экспоненты, которая играет важную роль в решении дифференциальных уравнений и анализе вариаций.

Использование константы «е» в математике распространено и широко применяется в научных и инженерных расчетах, моделировании, физике, экономике и других областях.

Число «е» в экспоненциальной функции

Экспоненциальная функция с основанием «е» имеет следующий вид:

ФормулаОписание

y = e^x

Экспоненциальная функция с основанием «е».

Экспоненциальная функция с основанием «е» обладает рядом интересных свойств:

• Её график проходит через точку с координатами (0, 1).
• Её производная равна самой функции: (d/dx)(e^x) = e^x.
• Её интеграл равен самой функции с постоянной: ∫(e^x)dx = e^x + C, где C – постоянная интегрирования.

Экспоненциальная функция с основанием «е» широко применяется в различных областях науки и техники, таких как физика, экономика, статистика и других. Она является одной из основных функций в математическом анализе и имеет множество приложений в решении различных задач.

Производная функции с «е»

Производная функции экспоненты с символом «е» имеет следующие основные свойства:

• Производная экспоненты равна самой экспоненте, то есть d/dx(e^x) = e^x.
• Производная экспоненты с постоянным множителем равна произведению экспоненты на этот множитель, то есть d/dx(a*e^x) = a*e^x, где a – постоянный множитель.
• Производная суммы экспонент равна сумме производных этих экспонент, то есть d/dx(e^x + e^y) = e^x + e^y.

Производная функции с символом «е» используется в различных областях математики и естественных наук, например, в физике, экономике, статистике и других. Она позволяет находить изменение функций, описывающих различные процессы, и анализировать их поведение в зависимости от переменных.

Логарифмическая функция с основанием «е»

Логарифмическая функция с основанием «е» обозначается как ln(x) или loge(x), где x — аргумент функции. Она является обратной к экспоненциальной функции, то есть позволяет найти значение аргумента, при котором функция принимает определенное значение.

Логарифмическая функция с основанием «е» обладает несколькими важными свойствами:

1. ln(1) = 0 — логарифм от единицы равен нулю;
2. ln(e) = 1 — логарифм от основания «е» равен единице;
3. ln(a * b) = ln(a) + ln(b) — логарифм произведения равен сумме логарифмов;
4. ln(an) = n * ln(a) — логарифм степени равен произведению степени и логарифма аргумента.

Применение логарифмической функции с основанием «е» находит в различных областях, таких как математика, физика, экономика и другие. Например, она используется для описания экспоненциального роста и упадка, решения дифференциальных уравнений, моделирования финансовых процессов и многое другое.

Комплексные числа и «е»

Символ «е» имеет особое значение в контексте комплексных чисел. Он представляет собой базисный элемент, используемый для записи комплексных чисел в тригонометрической форме.

Комплексные числа могут быть представлены в виде a + bi, где «a» — действительная часть, «b» — мнимая часть, и «i» — мнимая единица (i = √(-1)).

Одним из ключевых свойств символа «е» в контексте комплексных чисел является его связь с тригонометрической формой записи. Комплексное число z может быть выражено в виде z = r * (cosθ + i * sinθ), где r — модуль комплексного числа, θ — его аргумент.

Символ «е» также участвует в формуле Эйлера, которая связывает комплексные числа, тригонометрию и экспоненту. Формула Эйлера имеет вид e^(i * θ) = cosθ + i * sinθ.

Применение символа «е» в контексте комплексных чисел позволяет упростить вычисления и анализ различных математических задач, связанных с тригонометрией, электротехникой, квантовой физикой и другими областями науки.

Ряд Тейлора и «е»

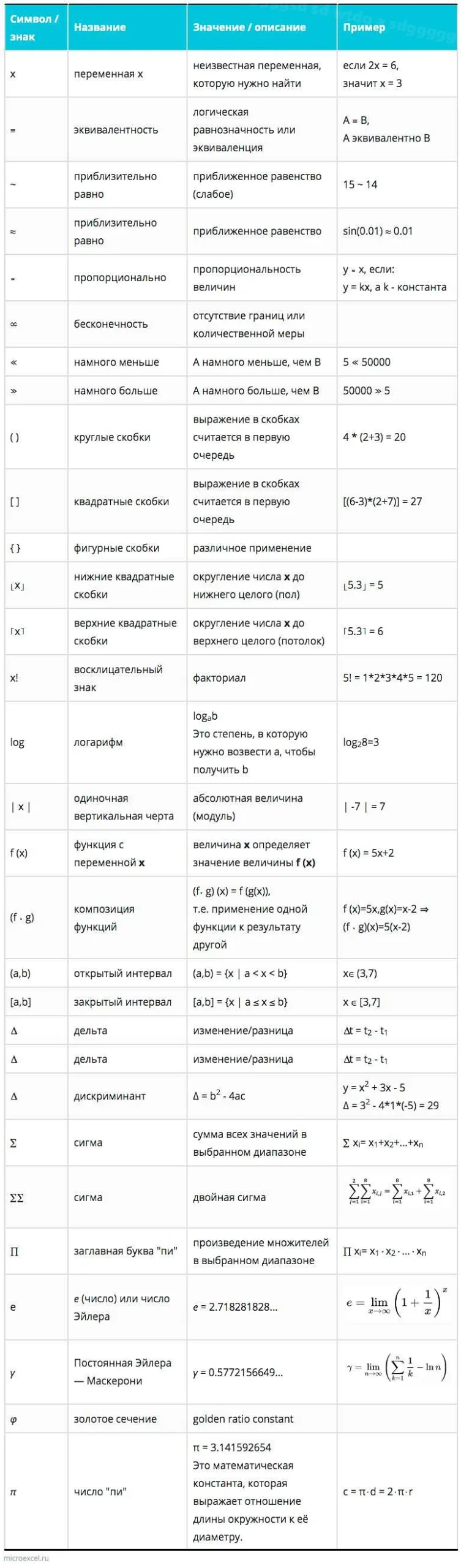
Важную роль в ряде Тейлора играет число «е» – основание натурального логарифма. Число «е» является иррациональным и трансцендентным, а его приближенное значение равно примерно 2,71828.

Ряд Тейлора для функции f(x) в окрестности точки x = a задается следующим образом:

f(x) = f(a) + f'(a)(x — a) + \frac{f»(a)}{2!}(x — a)^2 + \frac{f»'(a)}{3!}(x — a)^3 + \ldots

Здесь f'(a), f»(a), f»'(a) и т.д. обозначают производные функции f(x) в точке x = a.

Число «е» возникает в ряде Тейлора при аппроксимации экспоненциальной функции e^x. Для этой функции ряд Тейлора принимает следующий вид:

e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots

Этот ряд сходится для любого значения x и равен экспоненте e^x.

Таким образом, число «е» играет важную роль в математике, особенно в анализе и теории функций. Оно возникает при аппроксимации функций с помощью ряда Тейлора и имеет множество приложений в различных областях науки и техники.

Формула Эйлера и число «е»

Формула Эйлера выглядит следующим образом:

eiπ + 1 = 0

Здесь e — основание натурального логарифма, а i — мнимая единица. Число π представляет собой известное математическое константу — отношение длины окружности к ее диаметру.

Эта формула связывает пять основных математических констант: число «е», мнимую единицу, число π, число 0 и число 1. Она имеет глубокие физические и геометрические интерпретации и является одной из самых удивительных формул в математике.

Число «е» в формуле Эйлера играет особую роль. Оно является основанием натурального логарифма и имеет множество применений в различных областях науки и техники. Оно возникает в таких задачах, как моделирование роста популяции, распределение вероятности, анализ колебаний и многих других.

Число «е» также является одним из основных математических констант и часто встречается в различных формулах и уравнениях. Например, оно является основанием экспоненты и возникает в уравнении непрерывного процесса роста или убывания.

Таким образом, число «е» в формуле Эйлера имеет огромное значение в математике и науке. Оно позволяет связать различные области математики и физики, а его свойства и применение остаются активно изучаемыми и исследуемыми учеными.

Вопрос-ответ:

Вопрос

Ответ

Зачем в математике используется символ «е»?

Символ «е» в математике используется для обозначения числа Эйлера, основания натурального логарифма.

Какие свойства имеет символ «е» в математике?

Символ «е» обладает такими свойствами, как: эйлерова формула, экспоненциальная функция, пределы, связанные с числом «е».

Какое значение имеет символ «е» в экспоненциальной функции?

В экспоненциальной функции символ «е» обозначает основание экспоненты.

Как символ «е» связан с логарифмами?

Символ «е» связан с логарифмами через выражение e^x = ln(x), где «e» — основание натурального логарифма, а «ln» — натуральный логарифм.

Какие приложения имеет символ «е» в математике?

Символ «е» имеет множество приложений в математике, включая расчеты процентных ставок, моделирование роста и децентрализованных сетей, а также в физике и других науках.

Какое значение имеет символ «е» в математике?

Символ «е» в математике обозначает основание натурального логарифма, которое примерно равно 2,71828. Это число является иррациональным и трансцендентным.

Видео по теме: