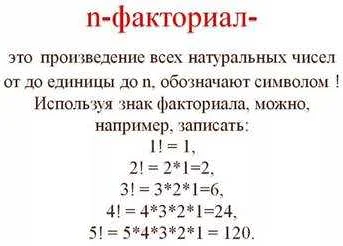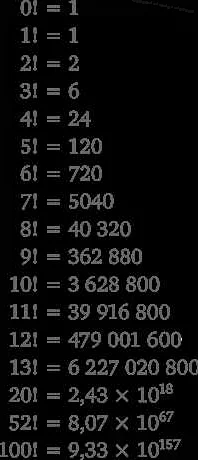Что означает знак подковы в математике

Знак подковы в математике — это символ, используемый для обозначения факториала числа. Он представляет собой укороченную версию математического выражения, которое показывает произведение всех целых чисел от 1 до данного числа. Узнайте, как использовать этот символ и его значения в математике.

Математика – это наука о числах, формулах, исследованиях и доказательствах. Однако она также полна символов и знаков, которые имеют определенное значение и применение. Один из таких знаков – знак подковы. В математике знак подковы используется для обозначения множества возможных решений, вероятности или условий, при которых можно достичь желаемого результата.

Знак подковы, как символ, имеет свою историю. В древнегреческой мифологии он ассоциировался с богиней удачи и счастья, Фортуной. Поэтому в математике знак подковы часто используется в задачах, связанных с вероятностью и удачей. Он также может быть использован для обозначения множества решений в уравнениях или системах уравнений.

Например, в задаче о бросании монеты, знак подковы может обозначать вероятность выпадения герба или орла. Если у нас есть две подковы, это может означать, что у нас есть две возможности: получить орла или герб. Таким образом, знак подковы помогает нам определить вероятность исхода события в математических задачах.

Значение и применение знака подковы в математике

Знак подковы в математике имеет специальное значение и применяется в различных контекстах. В данной статье рассмотрим основные сферы применения знака подковы и его значения.

Одно из основных значений знака подковы в математике – это обозначение операции умножения. Знак подковы часто используется для обозначения умножения в алгебре, геометрии и других разделах математики. Например, выражение 2 * 3 можно записать с использованием знака подковы как 2 × 3.

Знак подковы также может использоваться для обозначения диапазона чисел или переменных. Например, если нужно указать, что переменная x принимает значения от 1 до 10, можно записать это как x ∈ [1, 10]. Здесь знак подковы указывает на то, что переменная x принадлежит заданному диапазону.

Еще одним применением знака подковы в математике является обозначение открытого интервала. Например, если нужно указать, что переменная x принимает значения от 0 до 1, но не включая границы 0 и 1, можно записать это как x ∈ (0, 1). Знаки подковы указывают на то, что границы интервала не включаются в рассматриваемое множество значений.

Знак подковы также может быть использован для обозначения действительных чисел. Например, множество действительных чисел можно записать с использованием знака подковы как ℝ.

Примеры использования знака подковы в математикеЗначениеОбозначение

Умножение	2 × 3
Диапазон чисел	x ∈ [1, 10]
Открытый интервал	x ∈ (0, 1)
Действительные числа	ℝ

В заключение можно сказать, что знак подковы играет важную роль в математике и используется для обозначения различных операций и концепций. Знание и понимание значения и применения знака подковы помогает более точно и ясно выражать математические идеи и решения.

История и происхождение знака подковы

История и происхождение знака подковы связаны с развитием теории множеств и логики. Впервые знак подковы был введен и использован в математике в конце XIX века. Его введение связано с работами известного математика и логика Джорджа Буля.

Идея использования знака подковы для обозначения пересечения множеств возникла из аналогии с обычной подковой, которая пересекается с двумя плоскостями. Таким образом, знак подковы символизирует точку пересечения двух множеств.

С течением времени знак подковы стал широко распространенным и использовался во многих областях математики, таких как теория множеств, математическая логика, геометрия, топология и другие.

История и происхождение знака подковы являются важными аспектами изучения математики и позволяют лучше понять значение и применение этого символа в различных математических концепциях и теориях.

Математические свойства знака подковы

Вот некоторые основные математические свойства знака подковы:

1. Знак подковы может быть использован для обозначения отрицательных чисел. Например, если число -5 обозначается как «-5», то с использованием знака подковы оно будет выглядеть как «−5».
2. Знак подковы может быть использован для обозначения различных математических операций, таких как вычитание и отрицание. Например, выражение «a — b» может быть записано с использованием знака подковы как «a − b».
3. Знак подковы может быть использован для обозначения относительного значения переменной или числа. Например, если переменная «x» имеет значение -3, то она может быть записана с использованием знака подковы как «x = −3».
4. Знак подковы может быть использован для обозначения отрицательной степени числа. Например, число 2 в отрицательной степени может быть записано с использованием знака подковы как «2−1».

Таким образом, знак подковы играет важную роль в математике, обозначая относительные значения чисел и переменных, а также различные математические операции. Он позволяет более точно и ясно выражать математические концепции и идеи.

Применение знака подковы в алгебре

Знак подковы в алгебре используется для обозначения неравенства. Он ставится между двумя выражениями или числами и указывает на то, что первое выражение или число меньше второго.

В математике знак подковы обозначается символом »

Знак подковы широко используется в алгебре для сравнения чисел и переменных. Он позволяет установить отношение порядка между двумя значениями и определить, какое из них больше или меньше.

В алгебре знак подковы также используется для записи неравенств и неравенств с параметрами. Например, »

Применение знака подковы в алгебре позволяет упростить запись неравенств и установить их отношение между значениями. Он является неотъемлемой частью математической нотации и позволяет более точно и компактно описывать математические отношения.

ЗнакОписание

	Меньше
>	Больше
	Меньше или равно
>=	Больше или равно

Применение знака подковы в геометрии

Знак подковы может быть использован для обозначения отрезка между двумя точками на плоскости. В этом случае подкова помещается над двумя точками, между которыми находится отрезок. Также знак подковы может обозначать прямую или плоскость, которая ограничена двумя точками.

Применение знака подковы в геометрии позволяет конкретизировать и уточнить обозначение отрезков, прямых или плоскостей. Это удобно при проведении геометрических построений, решении задач и формулировке геометрических теорем и аксиом.

Кроме того, знак подковы может использоваться для обозначения угла. В этом случае подкова помещается между двумя отрезками, которые образуют данный угол. Такое обозначение позволяет удобно записывать геометрические свойства и формулы, связанные с углами.

Итак, знак подковы является важным и полезным символом в геометрии. Он позволяет более точно и ясно обозначать отрезки, прямые, плоскости и углы, что упрощает работу с геометрическими объектами и позволяет более точно формулировать геометрические теоремы и аксиомы.

Применение знака подковы в теории вероятностей

Таблица ниже демонстрирует пример использования знака подковы в теории вероятностей:

Событие AСобытие BУсловная вероятность P(A | B)

Солнечный день	Температура выше 30°C	P(A | B) = 0.8
Дождливый день	Температура выше 30°C	P(A | B) = 0.2
Солнечный день	Температура ниже 30°C	P(A | B) = 0.3
Дождливый день	Температура ниже 30°C	P(A | B) = 0.7

Таким образом, знак подковы позволяет более точно описывать вероятности событий в зависимости от других событий, что является важным инструментом в теории вероятностей.

Применение знака подковы в математическом анализе

В математическом анализе множества являются одним из основных объектов изучения. Они представляют собой совокупность элементов, которые обладают каким-то общим свойством. Для работы с множествами используются различные операции, и знак подковы играет важную роль при их обозначении.

Операция объединения множеств обозначается знаком подковы ∪. Она представляет собой операцию, при которой создается новое множество, включающее все элементы, принадлежащие хотя бы одному из исходных множеств. Например, если есть два множества A = {1, 2, 3} и B = {3, 4, 5}, то их объединение обозначается как A ∪ B и представляет собой множество {1, 2, 3, 4, 5}.

Операция пересечения множеств обозначается знаком подковы ∩. Она представляет собой операцию, при которой создается новое множество, содержащее только те элементы, которые принадлежат всем исходным множествам. Например, если есть два множества A = {1, 2, 3} и B = {3, 4, 5}, то их пересечение обозначается как A ∩ B и представляет собой множество {3}.

Знак подковы также может использоваться для обозначения других операций с множествами в математическом анализе, таких как разность множеств и симметрическая разность. Однако, его основное применение связано именно с операциями объединения и пересечения.

Применение знака подковы в дискретной математике

Знак подковы в дискретной математике используется для обозначения операции импликации. Он выражает логическое отношение, при котором из истинности одного высказывания следует истинность другого высказывания. Знак подковы обычно записывается в виде «→» или «->».

Операция импликации играет важную роль в доказательствах и логических выводах. Она позволяет строить логические цепочки, где каждое высказывание выводится из предыдущего. Например, если утверждение «если сегодня идет дождь, то улицы мокрые» истинно, а также утверждение «сегодня идет дождь» истинно, то можно заключить, что улицы мокрые.

Знак подковы также используется в формальных логиках и теории множеств. Он позволяет определить отношения между множествами и выражать логические операции, такие как объединение, пересечение и дополнение.

В дискретной математике знак подковы широко применяется при решении задач логики, алгоритмов и теории графов. Он помогает формализовать и структурировать высказывания, упрощает логические вычисления и доказательства, а также позволяет строить модели и алгоритмы для решения сложных задач.

Вопрос-ответ:

Каково значение знака подковы в математике?

В математике знак подковы обычно используется для обозначения факториала числа. Например, 5! (читается «пять факториал») означает произведение всех чисел от 1 до 5. То есть 5! = 5 * 4 * 3 * 2 * 1 = 120.

Какие еще применения имеет знак подковы в математике?

Помимо обозначения факториала, знак подковы можно использовать для обозначения перестановок и сочетаний. Например, если есть 5 различных предметов и нужно выбрать 3 из них, то количество сочетаний можно выразить как 5! / (3! * (5-3)!), где 5! — обозначение факториала числа 5.

Что происходит, когда знак подковы используется с отрицательным числом?

Знак подковы обычно применяется только к неотрицательным целым числам. Поэтому использование знака подковы с отрицательным числом не имеет определенного значения в обычной математике.

Можно ли использовать знак подковы для десятичных чисел?

Знак подковы обычно используется только для неотрицательных целых чисел. В случае десятичных чисел можно использовать гамма-функцию для вычисления аналогичных значений.

Какое значение имеет знак подковы в комбинаторике?

В комбинаторике знак подковы используется для обозначения факториала, перестановок и сочетаний. Факториал используется для вычисления числа возможных перестановок или сочетаний элементов. Это очень полезно при решении задач на вероятность, комбинаторику и теорию чисел.

Что означает знак подковы в математике?

В математике знак подковы обозначает факториал — произведение всех положительных целых чисел от 1 до данного числа.

Знак подковы в других областях математики

Знак подковы не только используется в алгебре и анализе, но и находит свое применение в других областях математики. Вот некоторые примеры:

1. Теория вероятностей: Знак подковы может быть использован для обозначения условной вероятности. Например, P(A | B), где A и B — события. Это показывает вероятность наступления события A при условии, что событие B уже произошло.
2. Теория графов: Знак подковы может быть использован для обозначения гамильтонова пути или цикла. Гамильтонов путь проходит через каждую вершину графа ровно один раз, а гамильтонов цикл — это гамильтонов путь, который начинается и заканчивается в одной и той же вершине.
3. Теория чисел: Знак подковы может быть использован для обозначения простого числа. Например, p — простое число. Простое число — это натуральное число, большее единицы, которое имеет только два делителя: 1 и само себя.
4. Комбинаторика: Знак подковы может быть использован для обозначения факториала числа. Например, n!. Факториал числа n — это произведение всех натуральных чисел от 1 до n.

Это лишь некоторые примеры использования знака подковы в других областях математики. Он является универсальным символом, который помогает обозначить различные математические концепции и свойства.

Видео по теме: