Что означает знак треугольник в математике

Знак треугольник в математике является символом для обозначения различных понятий и отношений, таких как геометрические фигуры, тригонометрические функции и неравенства. Узнайте, что означает треугольник и как он применяется в различных математических контекстах.

Треугольник является одной из самых важных геометрических фигур в математике. Он состоит из трех сторон и трех углов, и его форма напоминает букву «Т». Треугольник имеет многочисленные применения в различных областях математики, физики и других наук.

Одно из основных значений треугольника в математике — это его свойства и связанные с ними теоремы. Например, теорема Пифагора, гласящая, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов, является одной из наиболее известных и полезных теорем. Треугольники также играют важную роль в тригонометрии, где они используются для определения соотношений между углами и сторонами.

Кроме того, треугольник применяется для решения различных задач, связанных с измерением и конструированием. Например, посредством треугольника можно определить высоту недоступного объекта, используя принцип подобия треугольников. Также треугольник может быть использован для построения перпендикуляра, параллельных линий и других геометрических фигур.

В заключение, знание и понимание треугольника в математике имеет большое значение для решения различных задач и построения геометрических фигур. Треугольник обладает множеством свойств и теорем, которые помогают в решении задач, и его применение распространено в различных областях науки и техники.

Значение знака треугольник в математике

Одно из основных значений знака треугольник — это обозначение геометрического понятия треугольника. В геометрии, треугольник — это фигура, состоящая из трех отрезков, которые называются сторонами треугольника, и трех вершин, в которых стороны пересекаются. Знак треугольник используется для обозначения треугольника в геометрических диаграммах, формулах и уравнениях.

Кроме того, знак треугольник имеет значение в тригонометрии. Он используется для обозначения тригонометрических функций, таких как синус, косинус и тангенс. Например, синус угла обозначается символом sin и треугольником, который указывает на соответствующий угол в треугольнике, как на геометрическую интерпретацию этой функции.

Знак треугольник также может использоваться для обозначения отношений между сторонами и углами в треугольнике. Например, знак треугольник может указывать на равенство между двумя сторонами или равенство между двумя углами в треугольнике.

В общем, знак треугольник в математике широко используется для обозначения и символизации треугольников, тригонометрических функций и отношений между сторонами и углами. Он играет важную роль в геометрии, тригонометрии и других разделах математики.

Определение и общая информация

В математике треугольники могут быть классифицированы по различным свойствам, например, по длинам сторон и величинам углов. Существуют различные типы треугольников, такие как равносторонний, равнобедренный и разносторонний треугольник.

Знание свойств треугольников имеет широкое применение в различных областях, включая геометрию, физику, инженерное дело и архитектуру. Оно позволяет решать различные задачи, такие как вычисление площади треугольника, определение его высоты и нахождение значений углов.

Тип треугольникаОписание

Равносторонний треугольник	Все стороны равны
Равнобедренный треугольник	Две стороны равны
Разносторонний треугольник	Все стороны разные

Свойства и особенности треугольника

Основные свойства треугольника:

• Сумма всех углов треугольника равна 180 градусам.
• Сумма длин двух сторон треугольника всегда больше длины третьей стороны.
• Каждая сторона треугольника меньше суммы двух других сторон и больше их разности.
• Высота треугольника — это отрезок, который соединяет вершину треугольника с противоположной стороной и перпендикулярен этой стороне.
• Медиана треугольника — это отрезок, который соединяет вершину треугольника с серединой противоположной стороны.
• Биссектриса треугольника — это отрезок, который делит угол треугольника пополам и перпендикулярен противоположной стороне.
• Окружность, описанная вокруг треугольника (описанная окружность), проходит через все вершины треугольника.
• Окружность, вписанная в треугольник (вписанная окружность), касается всех сторон треугольника.

Треугольник является одной из основных и наиболее изучаемых фигур в геометрии. Его свойства и особенности широко применяются в различных областях, включая физику, инженерию, архитектуру и компьютерную графику.

Различные типы треугольников

Треугольники могут быть классифицированы на основе свойств их сторон и углов. Вот некоторые из наиболее распространенных типов треугольников:

Тип треугольникаОписание

Равносторонний треугольник	Все три стороны равны друг другу.
Равнобедренный треугольник	Две стороны равны друг другу.
Прямоугольный треугольник	Один из углов равен 90 градусам.
Остроугольный треугольник	Все углы острые (меньше 90 градусов).
Тупоугольный треугольник	Один из углов больше 90 градусов.

Знание этих типов треугольников помогает в решении геометрических задач и определении их свойств. Например, равносторонние и равнобедренные треугольники имеют специфические свойства, которые можно использовать для нахождения длин сторон и углов.

Теоремы и формулы, связанные с треугольником

В математике существует множество теорем и формул, которые связаны с треугольником. Некоторые из них являются основой для решения геометрических задач и имеют практическое применение в различных областях.

Одной из наиболее известных теорем, связанных с треугольником, является теорема Пифагора. Она утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2 = a2 + b2. Эта теорема находит применение в физике, инженерии и других науках.

Еще одной важной теоремой является теорема синусов. Она позволяет вычислить отношения сторон треугольника к синусам его углов. Формула для этой теоремы выглядит следующим образом: a/sin(A) = b/sin(B) = c/sin(C). Теорема синусов используется для решения различных задач, например, для нахождения недостающих сторон или углов треугольника.

Еще одной известной теоремой, связанной с треугольником, является теорема косинусов. Она позволяет вычислить длину одной из сторон треугольника, если известны длины двух других сторон и угол между ними. Формула для этой теоремы выглядит следующим образом: c2 = a2 + b2 — 2ab*cos(C). Теорема косинусов находит применение в геодезии, навигации и других областях.

Кроме того, существуют еще множество других теорем и формул, связанных с треугольником, таких как теорема о высотах, теорема о медианах, теорема о радиусе вписанной окружности и многие другие. Знание этих теорем и формул позволяет решать сложные геометрические задачи и углублять свои знания в математике.

Применение треугольника в геометрии и физике

Применение треугольника в геометрии:

ПрименениеОписание

Измерение углов	Треугольник используется для измерения углов и определения их типов (острый, прямой, тупой).
Вычисление площади	Площадь треугольника может быть вычислена с помощью формулы Герона или с использованием высоты и основания треугольника.
Нахождение высоты	Треугольник используется для определения высоты, которая является перпендикуляром, проведенным от вершины треугольника к основанию.
Решение подобия треугольников	Решение задач по подобию треугольников основано на соответствии их сторон и углов.

Треугольник также имеет важное значение в физике. Он используется для моделирования и изучения различных физических явлений и законов.

Применение треугольника в физике:

ПрименениеОписание

Разложение сил	Треугольник используется для разложения сил на составляющие и определения их векторных характеристик.
Определение углов	Треугольник используется для измерения углов и определения их значения в физических системах.
Решение задач динамики	Треугольник применяется для решения задач динамики, связанных с движением тел и взаимодействием сил.

Треугольник в тригонометрии и алгебре

В тригонометрии треугольник играет важную роль, так как углы и стороны треугольника могут быть использованы для определения тригонометрических функций, таких как синус, косинус и тангенс. С помощью этих функций можно решать различные задачи, связанные с геометрией и физикой.

В алгебре, треугольник может использоваться для решения систем уравнений или для определения значений переменных. Также треугольник может быть использован для представления геометрических диаграмм или графиков функций.

Тип треугольникаОпределение

Прямоугольный треугольник	Треугольник, у которого один из углов равен 90 градусам.
Равносторонний треугольник	Треугольник, у которого все стороны и углы равны.
Равнобедренный треугольник	Треугольник, у которого две стороны и два угла равны.

Знание свойств треугольников позволяет проводить различные математические доказательства и решать задачи. Оно также имеет широкое применение в инженерии, архитектуре и других областях, где требуется работа с геометрическими формами.

Графическое обозначение треугольника

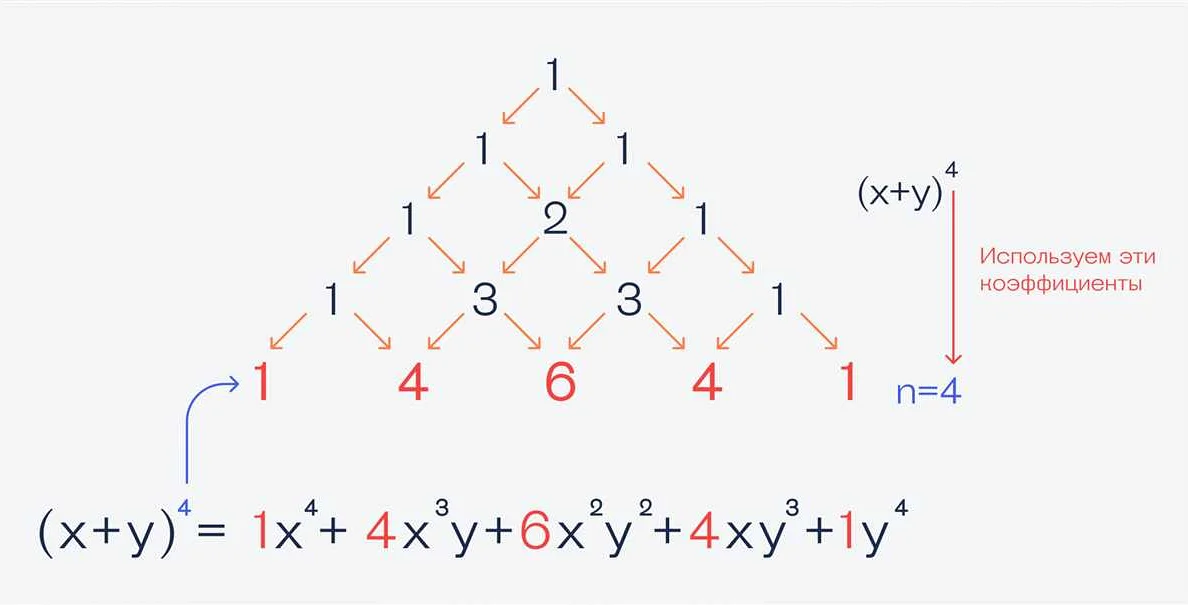
В обозначении треугольника используется знак треугольника, который представляет собой фигуру, состоящую из трех линий, соединяющихся в вершинах. Вершины треугольника обозначаются заглавными буквами, обычно A, B и C. Стороны треугольника обозначаются маленькими буквами, например, a, b и c, соответственно.

Графическое обозначение треугольника позволяет наглядно представить его форму и структуру, а также упрощает запись и описание свойств треугольника в математических формулах и уравнениях. Это обозначение также используется для обозначения различных типов треугольников, таких как равносторонний, равнобедренный, прямоугольный и другие.

Использование графического обозначения треугольника позволяет математикам и другим специалистам в области геометрии более удобно работать с треугольниками и проводить различные вычисления, а также изучать их свойства и отношения с другими фигурами.

Значение треугольника в символике и искусстве

В символике треугольник может иметь разные значения в зависимости от контекста. Один из наиболее распространенных символических смыслов треугольника — это его связь с тройственностью или триединством. В многих культурах треугольник ассоциируется с разделением на три части или с объединением трех элементов воедино.

В искусстве треугольник может быть использован для создания гармоничных композиций и передачи различных эмоций и настроений. Треугольники могут быть расположены в вертикальных, горизонтальных или диагональных линиях, создавая ощущение движения или стабильности. Они также могут быть использованы для создания глубины и перспективы в рисунке или живописи.

В некоторых случаях треугольник может иметь более специфическое значение, например, в символике масонства треугольник олицетворяет божественное совершенство и знание.

В искусстве и дизайне треугольник может быть использован как самостоятельный элемент или в сочетании с другими фигурами и символами. Он может быть использован для создания абстрактных композиций или для передачи определенного сообщения или идеи.

Таким образом, треугольник в символике и искусстве является мощным средством выражения и может иметь различные значения в зависимости от контекста и намерений автора.

Вопрос-ответ:

Зачем нужен знак треугольник в математике?

Знак треугольник в математике используется для обозначения геометрических фигур, а также для обозначения математических операций и отношений.

Какие геометрические фигуры обозначаются знаком треугольник?

Знак треугольника может обозначать треугольник, пирамиду, конус, пирамиду, а также другие фигуры, имеющие треугольную форму.

Какие математические операции и отношения обозначаются знаком треугольник?

Знак треугольника может обозначать операцию векторного умножения, скалярное произведение, неравенство, разностороннее неравенство, а также другие математические операции и отношения.

Какие еще значения может иметь знак треугольник в математике?

Знак треугольника может также означать показатель, градусник, треугольную матрицу, дельту (приращение), а также другие значения, зависящие от контекста.

В каких областях науки применяется знак треугольник?

Знак треугольник применяется в геометрии, алгебре, физике, статистике, математическом анализе, теории вероятности и других областях науки.

Видео по теме: