Что означает знак z в математике

Знак Z в математике, также известный как символ целых чисел, обозначает множество всех целых чисел, включая положительные, отрицательные и ноль. Узнайте, как использовать знак Z для обозначения целых чисел и как он используется в различных областях математики.

Знак z играет важную роль в математике и является одним из основных символов в этой науке. Он может использоваться в различных контекстах и иметь разные значения в зависимости от ситуации.

В теории множеств знак z может обозначать множество всех целых чисел. В этом контексте он широко используется для обозначения множества, содержащего все положительные и отрицательные целые числа, а также ноль.

В математическом анализе знак z может обозначать некоторую переменную или функцию. В этом случае он может принимать разные значения в зависимости от того, какие значения принимает эта переменная или функция.

Например, если z обозначает комплексное число, то он может иметь вид z = a + bi, где a и b — это вещественные числа, а i — мнимая единица.

Знак z также используется в статистике для обозначения стандартного отклонения. В этом контексте он показывает, насколько значения в выборке различаются от среднего значения.

Таким образом, знак z имеет множество значений и применений в математике. Он играет важную роль в различных областях этой науки и помогает упростить и структурировать математические выражения и уравнения.

Значение и применение знака z в математике

Знак «z» в математике имеет различные значения и применяется в разных областях.

В комплексном анализе «z» обозначает комплексное число и представляет собой сочетание вещественной и мнимой частей. Комплексные числа записываются в виде z = a + bi, где «a» — вещественная часть, «b» — мнимая часть, а «i» — мнимая единица, такая что i^2 = -1. Комплексные числа широко применяются в физике, инженерии, экономике и других науках, где они используются для описания и решения различных задач.

В некоторых областях математики, например в теории вероятностей и статистике, «z» может обозначать стандартное отклонение или нормально распределенную случайную величину. Он используется для измерения разброса значений и оценки вероятности появления определенного значения или диапазона значений.

В алгебре «z» может представлять собой переменную или неизвестную в уравнении. Она используется для обозначения неопределенных значений и решения уравнений с неизвестными.

Также «z» может использоваться в геометрии для обозначения координаты точки в двумерной плоскости. В этом случае «z» представляет собой пару (x, y), где «x» — горизонтальная координата и «y» — вертикальная координата.

Исходя из вышесказанного, знак «z» играет важную роль в математике и является неотъемлемой частью различных математических концепций и приложений.

Видео по теме:

Определение и основные характеристики знака z

Знак z обычно используется для обозначения комплексных чисел. Комплексные числа представляют собой комбинацию действительной и мнимой части, и их обозначение часто включает использование буквы z. Например, z = a + bi, где a — действительная часть, b — мнимая часть, i — мнимая единица.

Знак z также может быть использован для обозначения координатной оси в трехмерной системе координат. Когда используется в этом контексте, z обычно представляет третью ось, перпендикулярную к плоскости, образованной другими двумя осями, обозначаемыми x и y.

В некоторых областях математики, таких как комплексный анализ или теория вероятностей, z также может использоваться в качестве обозначения переменной или функции. Здесь его использование может быть специфичным для конкретной теории или области исследования.

В заключение, знак z в математике является важным символом, который используется для обозначения различных переменных, комплексных чисел или координатных осей. Его использование и значения могут варьироваться в зависимости от контекста и конкретной математической дисциплины.

Значение знака z в алгебре и геометрии

Знак z в алгебре и геометрии может иметь различные значения в зависимости от контекста.

В алгебре, знак z обычно используется для обозначения переменной или неизвестного значения. Он может представлять любое число или выражение, которое мы еще не знаем. Используя знак z, мы можем задавать и решать уравнения, составлять формулы и проводить различные математические операции.

В геометрии, знак z может обозначать координату или положение точки в трехмерном пространстве. Координаты точек в трехмерной системе координат обычно обозначаются буквами x, y и z. Значение z-координаты позволяет нам определить, насколько высоко или низко находится точка относительно плоскости или оси.

Также знак z может использоваться для обозначения комплексных чисел в алгебре. Комплексное число представляет собой комбинацию вещественной и мнимой частей, где мнимая часть обозначается буквой i. Знак z обозначает комплексное число в общем случае, где z = a + bi, где a и b — вещественные числа, а i — мнимая единица.

ЗначениеОписание

переменная	неизвестное значение в алгебре
координата	положение точки в геометрии
комплексное число	комбинация вещественной и мнимой частей

Вопрос-ответ:

Что такое знак z в математике?

Знак z в математике используется для обозначения некоторых величин, таких как комплексные числа или переменные в уравнениях.

Какие значения может принимать знак z?

Знак z может принимать различные значения в зависимости от контекста. В математике он может обозначать комплексные числа, координату на комплексной плоскости или переменную в уравнении.

Для чего используется знак z в комплексных числах?

Знак z в комплексных числах обозначает их мнимую часть. Комплексные числа представляются в виде a + bi, где a — действительная часть числа, а bi — мнимая часть, где z = bi.

Какие свойства имеет знак z в математике?

Знак z в математике обладает рядом свойств. Например, если z1 и z2 — комплексные числа, то их сумма z1 + z2 будет также комплексным числом. Также знак z может принимать значения в комплексной плоскости и использоваться для решения уравнений.

Какие применения имеет знак z в математике?

Знак z в математике имеет множество применений. Он используется для работы с комплексными числами, решения уравнений, анализа электрических цепей и многих других областей. Кроме того, знак z может быть использован для обозначения переменных в математических формулах и уравнениях.

Зачем в математике используется знак z?

Знак z в математике используется для обозначения комплексных чисел. Комплексные числа состоят из действительной и мнимой частей и представляют собой комбинацию чисел вида a + bi, где a и b — действительные числа, а i — мнимая единица. Знак z позволяет наглядно обозначить комплексные числа и проводить операции с ними.

Какие значения может принимать знак z в математике?

Знак z в математике может принимать различные значения в зависимости от контекста. В частности, в алгебре знак z может обозначать комплексное число или переменную. В тригонометрии знак z может обозначать аргумент комплексного числа. В анализе знак z может обозначать независимую переменную. В общем случае, значение знака z определяется контекстом и обозначает некоторый элемент или переменную в математической системе.

Применение знака z в статистике и вероятности

В статистике знак z используется для преобразования исходных данных в стандартные единицы. Это позволяет сравнивать разные наборы данных и проводить статистические анализы. Значение z-оценки показывает, насколько отклоняется наблюдаемое значение от среднего значения исходной выборки.

Вероятность в области статистики и вероятности часто связана с нормальным распределением. Знак z используется для определения площади под кривой нормального распределения и вычисления вероятностей событий. При известном среднем значении и стандартном отклонении, знак z может быть использован для определения вероятности того, что значение попадет в определенный диапазон или будет выше/ниже определенного значения.

Также знак z является важным инструментом в проведении статистических тестов, таких как t-тесты и анализ дисперсии. Он позволяет сравнивать различные группы и определять, являются ли различия между ними статистически значимыми.

В целом, знак z играет ключевую роль в статистике и вероятности, обеспечивая анализ данных, оценку вероятностей и проведение статистических тестов. Он позволяет исследователям делать выводы на основе данных и сравнивать результаты разных исследований.

Знак z в теории чисел и комбинаторике

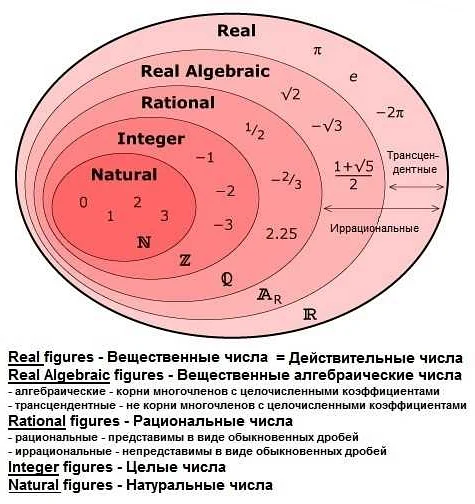
Знак z также находит свое применение в теории чисел и комбинаторике. В этих областях математики знак z используется для обозначения различных величин и свойств чисел и комбинаций.

В теории чисел знак z может обозначать целое число, которое имеет определенные свойства или выполняет определенные условия. Например, знак z может обозначать простые числа, которые делятся только на себя и на 1. Также знак z может обозначать числа Фибоначчи, которые определяются рекурсивной формулой zn = zn-1 + zn-2.

В комбинаторике знак z может обозначать количество комбинаций или перестановок. Например, z! обозначает факториал числа z, который представляет собой произведение всех натуральных чисел от 1 до z. Знак z может также обозначать биномиальные коэффициенты, которые используются при подсчете числа сочетаний k элементов из множества из z элементов.

Таким образом, знак z играет важную роль в теории чисел и комбинаторике, помогая обозначать и описывать различные числовые величины и комбинации.

Роль знака z в матричных вычислениях

Знак z также используется для обозначения переменной или неизвестного элемента матрицы. В матричных операциях, таких как сложение, вычитание, умножение и деление, знак z позволяет удобно обозначать и оперировать с неизвестными элементами матрицы.

Кроме того, знак z используется для обозначения векторов или столбцов в матрицах. Векторы могут быть представлены как столбцы или строки матрицы, и знак z позволяет удобно обозначать векторные элементы и выполнять операции с ними.

Использование знака z в матричных вычислениях существенно упрощает запись и решение систем линейных уравнений, а также позволяет более эффективно работать с матрицами в области линейной алгебры.

Знак z в физике и инженерных расчетах

Знак z широко используется в физике и инженерных расчетах для обозначения координаты или величины, обычно относящейся к вертикальной оси системы координат. В физике, например, в механике и электродинамике, z-координата может указывать на глубину или высоту. В инженерных расчетах, например, в строительстве и геодезии, знак z может обозначать отметку или высоту точки относительно определенного уровня.

В физике, знак z часто используется в трехмерных системах координат, где он обозначает ось, перпендикулярную плоскости xy. Например, в классической механике, z-координата может указывать на вертикальную позицию тела в пространстве. Также знак z может использоваться для обозначения компоненты вектора или других величин, относящихся к этой оси.

В инженерных расчетах, знак z может иметь различные значения в зависимости от предметной области и используемой системы координат. Например, в строительстве, знак z может обозначать высоту здания или поверхности земли относительно определенного уровня. В геодезии, знак z может использоваться для указания глубины точки под поверхностью земли или моря.

Использование знака z в физике и инженерных расчетах является универсальным и позволяет однозначно обозначать вертикальную компоненту величин или координат в трехмерном пространстве. Он играет важную роль в различных научных и технических областях, обеспечивая точное описание и анализ различных физических процессов и инженерных систем.

Примеры использования знака z:

Механика: z-координата точки на вертикальной оси

Электродинамика: z-компонента электрического или магнитного поля

Строительство: z-координата отметки здания или поверхности земли

Геодезия: z-координата глубины точки под поверхностью земли или моря

Применение знака z в компьютерных науках и программировании

Знак z широко используется в компьютерных науках и программировании для обозначения различных величин и операций. Вот некоторые из основных областей, где применяется знак z:

• Комплексные числа: В компьютерных науках и математике знак z используется для обозначения мнимой единицы, в комплексных числах запись a + bi, где a и b — действительные числа, а i — мнимая единица.
• Статистика: В статистике знак z обозначает стандартное отклонение. Он используется для измерения разброса значений в выборке относительно среднего значения.
• Алгоритмы и структуры данных: В алгоритмах и структурах данных знак z может использоваться для обозначения временной сложности или пространственной сложности алгоритма или структуры данных.
• Графика и визуализация: В графике и визуализации знак z может обозначать координату оси z в трехмерном пространстве. Он используется для представления трехмерных объектов и их положения.
• Компьютерная графика: В компьютерной графике знак z может использоваться для обозначения глубины пикселя или точки в трехмерном пространстве. Он используется для создания эффекта глубины и реалистичности изображений.
• Статический анализ кода: В программировании знак z может использоваться для обозначения переменных, функций или классов, которые имеют особое значение или свойство.

Это только некоторые примеры применения знака z в компьютерных науках и программировании. Знак z является важным инструментом в этих областях и помогает разработчикам и исследователям более точно описывать и моделировать различные явления и процессы.