Отношение какой знак в математике
Содержимое
- 1 Отношение какой знак в математике
- 1.1 Отношение в математике: что это такое?
- 1.2 Симметричность
- 1.3 Отношение симметрично: примеры
- 1.4 Транзитивность
- 1.5 Отношение транзитивно: основные понятия
- 1.6 Антисимметричность
- 1.7 Отношение антисимметрично: примеры использования
- 1.8 Рефлексивность
- 1.9 Отношение рефлексивно: основные свойства
- 1.10 Эквивалентность
- 1.11 Вопрос-ответ:
- 1.12 Видео по теме:
Знак отношения в математике представляет собой символ, который показывает соотношение между двумя числами или выражениями. В данной статье рассматривается значение и использование различных знаков отношения, таких как равенство, больше, меньше, больше или равно, меньше или равно и т.д. Узнайте, как правильно интерпретировать и применять эти знаки для сравнения и установления отношений между числами и выражениями.
В математике отношение – это понятие, которое связывает два элемента множества и определяет их взаимосвязь. Оно помогает нам сравнивать, классифицировать и анализировать различные объекты и явления. Отношение обозначается специальным знаком, который выражает связь между элементами.
Существуют различные виды отношений в математике. Например, отношение равенства, которое обозначается знаком «=» и утверждает, что два элемента множества равны друг другу. Отношение неравенства, обозначаемое знаками «≠», «», устанавливает, что один элемент множества больше или меньше другого.
Также существуют более сложные отношения, например, отношение порядка или отношение эквивалентности. Отношение порядка обозначается знаками «=» и говорит о том, что один элемент множества находится в определенном отношении с другим, например, больше или меньше. Отношение эквивалентности, обозначаемое знаком «≡», устанавливает, что два элемента множества считаются эквивалентными друг другу.
Примеры отношений в математике можно найти во множестве различных областей, таких как алгебра, геометрия, теория вероятностей и другие. Например, отношение «больше или равно» используется для сравнения чисел, отношение «вложено» применяется в геометрии для определения, какие фигуры содержатся внутри других, а отношение «взаимно исключающие» применяется в теории вероятностей для описания событий, которые не могут произойти одновременно.
Понимание отношений в математике является ключевым для решения различных задач и построения логических выводов. Важно уметь анализировать и интерпретировать различные отношения, чтобы применять их на практике и использовать в решении реальных проблем.
Отношение в математике: что это такое?
Отношение обычно обозначается символом «R» и записывается в виде (a, b)∈R, где «a» и «b» — элементы двух множеств. Это означает, что элемент «a» находится в определенной связи с элементом «b».
Отношения в математике могут быть различными: равенство, неравенство, принадлежность, подмножество и т. д. Например, отношение равенства определяет, что два элемента множества равны между собой, и обозначается символом «=».
Отношения в математике могут быть также классифицированы по своим свойствам, например, симметричность, рефлексивность, транзитивность. Симметричное отношение означает, что если элемент «a» связан с элементом «b», то элемент «b» также связан с элементом «a». Рефлексивное отношение означает, что каждый элемент множества связан с собой. Транзитивное отношение означает, что если элемент «a» связан с элементом «b» и элемент «b» связан с элементом «c», то элемент «a» также связан с элементом «c».
Отношения в математике широко используются в различных областях, таких как алгебра, геометрия, теория множеств и т. д. Они позволяют анализировать и описывать связи между объектами и являются важным инструментом для решения математических задач.
Симметричность
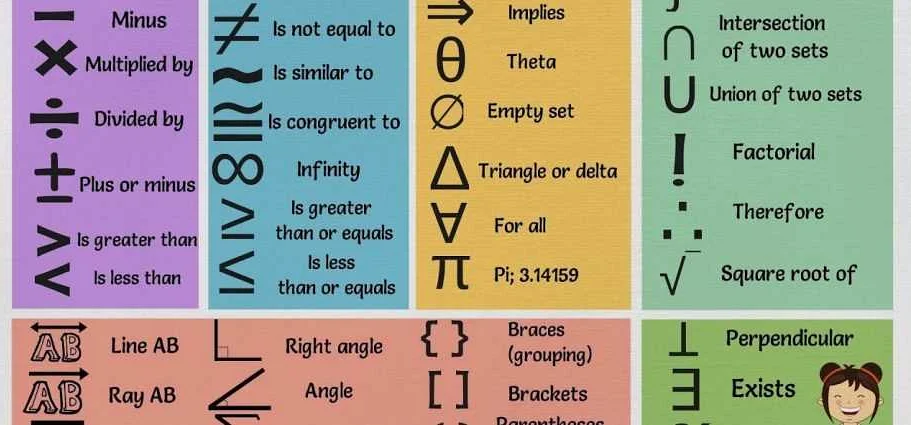
Примером симметричного отношения является отношение «равенство». Если два элемента A и B равны между собой, то и B равен A.
Для наглядности можно представить симметричное отношение в виде таблицы, где по вертикали и горизонтали указаны элементы множества, а в ячейках таблицы указывается, связаны ли эти элементы. Если отношение симметрично, то таблица будет симметричной относительно главной диагонали.
A
B
C
ABC
| Да | Нет | Нет |
| Нет | Да | Нет |
| Нет | Нет | Да |
В данном примере отношение симметрично, так как каждая пара элементов имеет симметричную пару в таблице.
Отношение симметрично: примеры
В математике отношение называется симметричным, если для любых двух элементов, принадлежащих множеству, существует обратное отношение, связывающее их. То есть, если для элементов a и b справедливо отношение aRb, то также справедливо и отношение bRa.
Примеры симметричных отношений:
- Отношение «равенство»: если a = b, то также b = a.
- Отношение «совпадение»: если два объекта полностью совпадают, то это симметричное отношение.
- Отношение «эквивалентность»: если два объекта эквивалентны друг другу, то это симметричное отношение.
В дополнение к этим примерам, симметричные отношения могут быть обнаружены в различных областях математики и физики.
Транзитивность
В математике отношение называется транзитивным, если для любых трех элементов, находящихся в этом отношении, если первый элемент связан с вторым элементом и второй элемент связан с третьим элементом, то первый элемент связан с третьим элементом. Другими словами, если \(a\) связано с \(b\) и \(b\) связано с \(c\), то \(a\) связано с \(c\).
Транзитивность является одним из основных свойств отношений и имеет широкое применение в различных областях математики, таких как алгебра, графы и логика.
Например, рассмотрим отношение «больше» на множестве натуральных чисел. Если \(a\) больше \(b\) и \(b\) больше \(c\), то можно сделать вывод, что \(a\) больше \(c\). Это свойство отношения «больше» называется транзитивностью и позволяет устанавливать порядок чисел.
Другим примером транзитивного отношения является отношение эквивалентности. Если два элемента эквивалентны друг другу, и второй элемент эквивалентен третьему элементу, то можно сделать вывод, что первый элемент эквивалентен третьему элементу. Это свойство позволяет классифицировать объекты на эквивалентные классы и использовать их в различных областях математики и науки.
Отношение транзитивно: основные понятия

Транзитивность — это свойство отношения, которое означает, что если элемент A связан с элементом B, а элемент B связан с элементом C, то элемент A также связан с элементом C.
Другими словами, если у нас есть отношение R и элементы a, b и c, такие что (a, b) ∈ R и (b, c) ∈ R, то (a, c) ∈ R.
Например, рассмотрим отношение «больше» на множестве целых чисел. Если число A больше числа B, а число B больше числа C, то число A также больше числа C. Это пример транзитивного отношения.
Антисимметричность
Другими словами, антисимметричность означает, что если два элемента связаны отношением, то они не могут быть одновременно связаны друг с другом в обратном порядке. Например, если элементы $a$ и $b$ связаны отношением «больше или равно», то если $a \geq b$ и $b \geq a$, то $a$ и $b$ должны быть равны.
Антисимметричность широко применяется в алгебре, теории множеств, графовой теории и других областях математики. Она позволяет установить четкую и строгую связь между элементами множества, что помогает в анализе и решении различных задач и проблем.
Примеры отношений, обладающих антисимметричностью:
- Отношение «меньше или равно» между числами: если $a \leq b$ и $b \leq a$, то $a$ и $b$ равны.
- Отношение «подмножество» между множествами: если $A \subseteq B$ и $B \subseteq A$, то $A$ и $B$ равны.
- Отношение «делится без остатка» между числами: если $a \mid b$ и $b \mid a$, то $a$ и $b$ равны.
Антисимметричность является важным свойством отношений и позволяет строить логические выводы и утверждения на основе данных отношений.
Отношение антисимметрично: примеры использования

В математике отношение называется антисимметричным, если из выполнения условия «aRb» и «bRa» следует, что «a = b». Другими словами, если элементы множества связаны отношением R и если одновременно связаны обратным отношением R, то это означает, что эти элементы равны.
Примером антисимметричного отношения может служить отношение «≤» на множестве натуральных чисел. Если число a меньше или равно числу b (a ≤ b) и одновременно число b меньше или равно числу a (b ≤ a), то это означает, что a равно b (a = b).
Другим примером может служить отношение «включает в себя» на множествах. Если множество A включает в себя множество B (A ⊆ B) и одновременно множество B включает в себя множество A (B ⊆ A), то это означает, что множества A и B равны (A = B).
Антисимметричные отношения широко используются в различных областях математики, логики и информатики. Они позволяют устанавливать соответствия и связи между элементами множеств и использовать их для решения различных задач и проблем.
Рефлексивность
Например, отношение «больше или равно» является рефлексивным, так как каждое число больше или равно самому себе. То есть для любого числа «а» отношение «а, а» будет истинным.
Рефлексивность является одним из основных свойств отношений и широко применяется в различных областях математики и логики.
Отношение рефлексивно: основные свойства
В математике отношение называется рефлексивным, если каждый элемент множества A связан с самим собой. То есть для каждого элемента a из множества A выполняется условие aRa.
Основные свойства рефлексивного отношения:
- Каждый элемент множества A связан с самим собой.
- Для любого элемента a из множества A, пара (a, a) принадлежит отношению.
- Отношение является замкнутым на множестве A.
Примеры рефлексивных отношений:
- Отношение «быть равным» на множестве целых чисел. Каждое целое число равно самому себе.
- Отношение «иметь общий делитель» на множестве натуральных чисел. Каждое натуральное число имеет общий делитель с самим собой (например, 5 и 5).
Рефлексивность является одним из основных свойств отношений и играет важную роль в различных областях математики и науки.
Эквивалентность
Эквивалентность может быть определена на основе различных критериев. Например, два алгебраических выражения могут быть эквивалентными, если они имеют одинаковую форму или свойства. Это означает, что они дают одинаковый результат при любых значениях переменных.
Также эквивалентность может быть определена в контексте логических выражений или утверждений. Два логических выражения будут эквивалентными, если они имеют одинаковые истинностные значения для всех возможных комбинаций значений их компонентов.
Примеры эквивалентности в математике:
- Выражения «2 + 3» и «5» эквивалентны, так как они дают одинаковый результат.
- Выражения «(x + y)²» и «x² + 2xy + y²» эквивалентны в алгебре, так как они имеют одинаковую форму.
- Утверждения «Если сегодня идет дождь, то улицы мокрые» и «Если улицы мокрые, то сегодня идет дождь» эквивалентны с точки зрения логики, так как они имеют одинаковые истинностные значения.
Эквивалентность является важным понятием в математике, так как позволяет упрощать выражения, доказывать теоремы и устанавливать связи между различными математическими объектами.
Вопрос-ответ:
Какие основные понятия связаны с отношением в математике?
Основные понятия, связанные с отношением в математике, включают множества, упорядоченные пары, отношения эквивалентности и отношения порядка.
Что такое множества в математике?
В математике множество — это коллекция уникальных элементов, которые могут быть числами, буквами или другими объектами.
Что такое упорядоченные пары?
Упорядоченная пара — это пара элементов, где порядок элементов имеет значение. Например, пара (1, 2) отличается от пары (2, 1).
Что такое отношение эквивалентности?
Отношение эквивалентности — это отношение, которое устанавливает эквивалентность между элементами множества. Это означает, что элементы считаются равными или эквивалентными друг другу.
Какие примеры отношений можно привести в математике?
Примеры отношений в математике включают отношение «больше» или «меньше» в числовом порядке, отношение эквивалентности между классами эквивалентности и отношение «является подмножеством» между множествами.
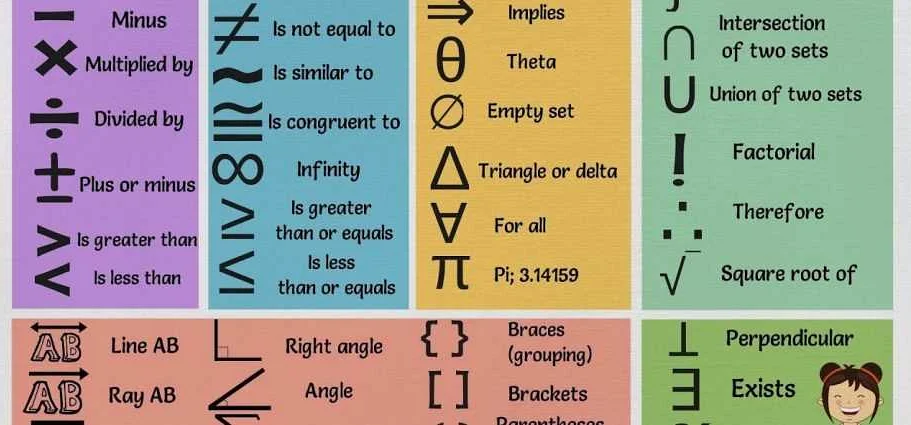

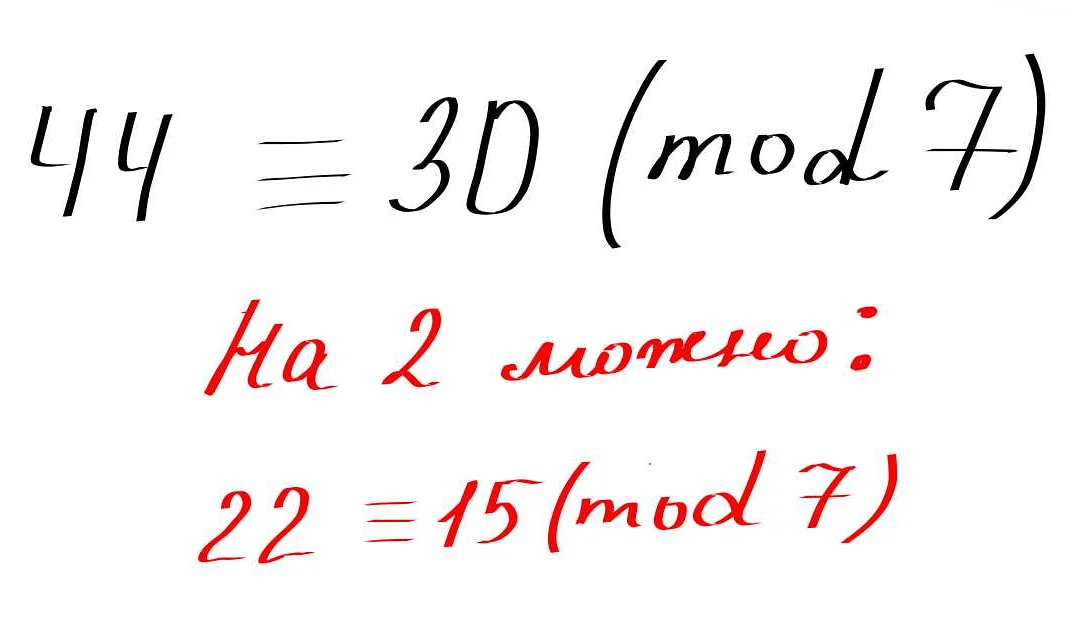


Отношение – одно из важнейших понятий в математике. Оно позволяет сравнивать и связывать различные числа или объекты. Например, знак «больше» (>) указывает на то, что одно число превосходит другое, а знак «меньше» (
Статья очень понятно и доступно объясняет основные понятия отношений в математике. Мне очень понравилось, как автор подходит к объяснению сложных тем, используя простые и наглядные примеры. Теперь я наконец-то понимаю, как работают отношения на практике и как их применять в решении различных задач. Эта статья поможет мне улучшить мои навыки в математике и лучше понимать эту науку. Большое спасибо автору за такую полезную и интересную статью! Жду с нетерпением новых материалов.