Что такое абсолютная частота в математике

Абсолютная частота в математике — это количество раз, которое определенное значение появляется в наборе данных. Она позволяет измерить, насколько часто конкретное значение встречается в совокупности данных и является важной характеристикой для анализа распределения данных.

В математике абсолютная частота является одним из основных понятий статистики. Она определяет количество раз, которое конкретное значение встречается в наборе данных. Абсолютная частота позволяет оценить, насколько часто происходит определенное явление или событие, и является одним из важных инструментов для анализа данных.

Для вычисления абсолютной частоты необходимо взять набор данных и посчитать количество раз, которое каждое значение встречается в этом наборе. Например, если у нас есть список оценок студентов по математике: 4, 5, 3, 4, 4, 5, то абсолютная частота оценки 4 равна 3, а оценки 5 — 2.

Абсолютная частота является важным инструментом для анализа данных, так как она позволяет установить, какие значения встречаются чаще других и какое явление происходит более или менее часто. Это позволяет сделать выводы и принять решения на основе полученных данных.

Использование абсолютной частоты в математике не только помогает понять наличие определенных закономерностей или тенденций, но и является неотъемлемой частью проведения исследований и статистического анализа данных. Знание абсолютных частот позволяет сравнить различные значения и определить, какие события или явления более или менее вероятны.

В заключение, абсолютная частота — это важное понятие в математике, которое позволяет оценивать частоту появления конкретных значений в наборе данных. Ее использование помогает проводить статистический анализ, выявлять закономерности и делать выводы на основе полученных данных.

Что такое абсолютная частота?

Для вычисления абсолютной частоты необходимо просмотреть каждый элемент набора данных и подсчитать, сколько раз данный элемент встречается. Это может быть сделано вручную или с использованием программного обеспечения для статистического анализа данных.

Примером использования абсолютной частоты может быть анализ текстового документа. Представим, что у нас есть набор данных, состоящий из различных слов, используемых в тексте. Мы можем использовать абсолютную частоту для определения, сколько раз каждое слово встречается в тексте. Это позволит нам определить наиболее часто используемые слова и провести дополнительный анализ текста.

Абсолютная частота является важным инструментом для анализа данных в различных областях, таких как статистика, наука о данных, маркетинг и другие. Она помогает нам понять распределение значений в наборе данных и выявить наиболее часто встречающиеся элементы. Это дает нам возможность сделать выводы и принять решения на основе этих данных.

Видео по теме:

Формула для расчета абсолютной частоты

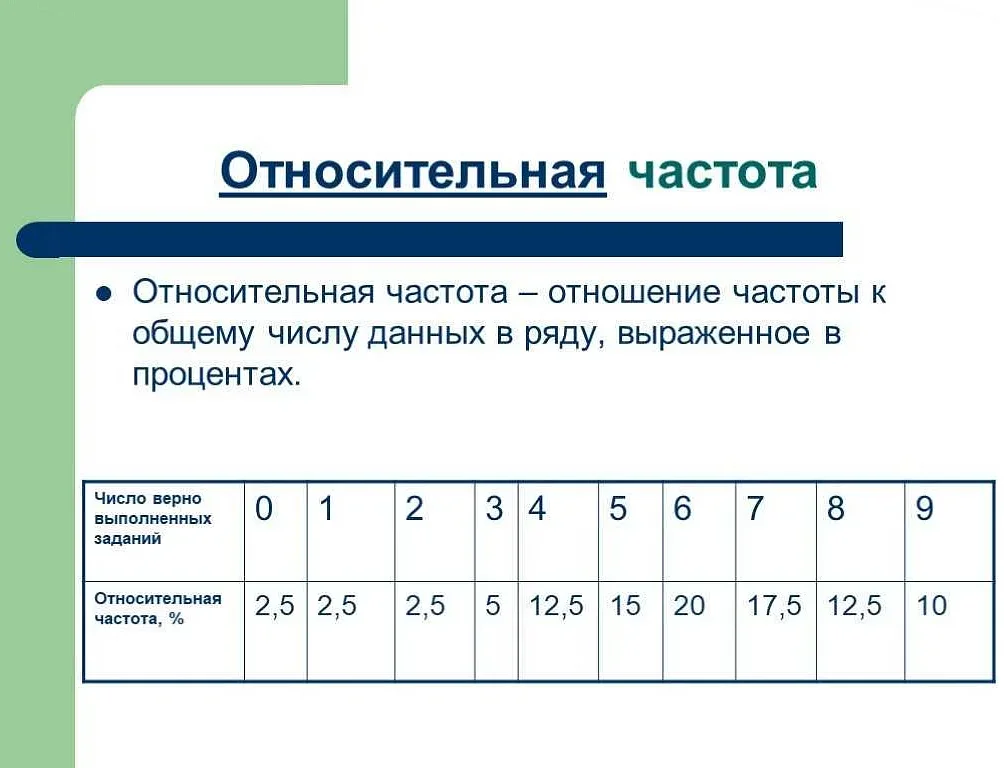
СимволОписание

n	Количество наблюдений
f	Абсолютная частота
x	Значение

Формула для расчета абсолютной частоты:

f = n(x)

Где:

• f — абсолютная частота;
• n — количество наблюдений;
• x — значение.

Пример расчета абсолютной частоты:

Представим, что у нас есть набор данных, состоящий из чисел 2, 3, 5, 2, 4. Найдем абсолютную частоту для числа 2:

В данном случае:

• n = 5 (общее количество наблюдений);
• x = 2 (значение).

Используя формулу абсолютной частоты, получим:

f = 5(2) = 2

Таким образом, абсолютная частота числа 2 равна 2.

Как абсолютная частота используется в статистике

Абсолютная частота в математике представляет собой количество раз, которое определенное значение или событие встречается в наборе данных. В статистике абсолютная частота используется для измерения встречаемости определенных значений или событий и позволяет проводить анализ и сравнение данных.

Абсолютная частота может использоваться для изучения распределения значений в наборе данных. Например, при исследовании результатов опроса, абсолютная частота может показать, сколько человек отвечали на каждый вопрос опроса, что позволяет выявить наиболее популярные и наименее популярные ответы.

Также абсолютная частота может использоваться для создания гистограммы или столбчатой диаграммы, которая визуально отображает количество раз, которое каждое значение встречается в наборе данных. Это позволяет наглядно представить распределение данных и выявить любые особенности или тренды.

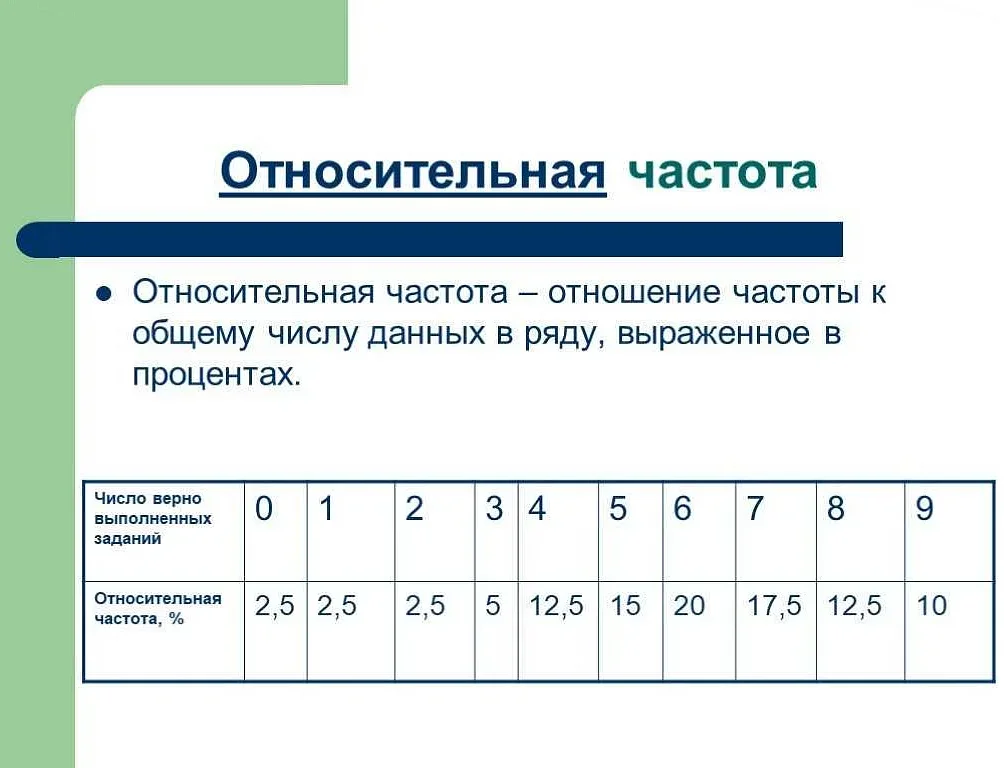
Абсолютная частота может быть полезна также при проведении статистического анализа данных. Она может быть использована для вычисления других показателей, таких как относительная частота или процентное соотношение. Например, зная абсолютную частоту каждого значения, можно вычислить его относительную частоту, разделив абсолютную частоту на общее количество наблюдений.

Таким образом, абсолютная частота является важным инструментом для анализа и интерпретации данных в статистике. Она помогает выявить распределение значений, сравнить данные и провести статистический анализ. Понимание и использование абсолютной частоты позволяет получить более глубокое представление о данных и сделать более обоснованные выводы.

Вопрос-ответ:

Что такое абсолютная частота в математике?

Абсолютная частота в математике — это количество раз, которое определенное значение появляется в наборе данных.

Как можно вычислить абсолютную частоту?

Абсолютную частоту можно вычислить путем подсчета количества раз, которое определенное значение встречается в наборе данных.

В каких случаях используется абсолютная частота в математике?

Абсолютная частота используется в математике для анализа данных и позволяет определить, сколько раз значение появляется в наборе данных.

Можете привести пример использования абсолютной частоты?

Конечно! Например, если у нас есть набор данных, состоящий из оценок студентов на экзамене (3, 4, 4, 5, 5, 5), то абсолютная частота оценки «5» будет равна 3, так как она появляется 3 раза в наборе данных.

В чем разница между абсолютной частотой и относительной частотой?

Разница между абсолютной частотой и относительной частотой заключается в том, что абсолютная частота показывает количество раз, которое значение появляется в наборе данных, в то время как относительная частота показывает долю или процентное соотношение значения относительно всего набора данных.

Примеры абсолютной частоты в математике

Пример 1: Рассмотрим набор данных о количестве семейных автомобилей в десяти различных городах. Подсчитаем абсолютную частоту количества автомобилей в наборе данных:

Город 1: 100 автомобилей

Город 2: 75 автомобилей

Город 3: 120 автомобилей

Город 4: 90 автомобилей

Город 5: 110 автомобилей

Город 6: 80 автомобилей

Город 7: 105 автомобилей

Город 8: 95 автомобилей

Город 9: 85 автомобилей

Город 10: 100 автомобилей

Теперь мы можем подсчитать абсолютную частоту для каждого значения:

Абсолютная частота для 100 автомобилей — 2

Абсолютная частота для 75 автомобилей — 1

Абсолютная частота для 120 автомобилей — 1

Абсолютная частота для 90 автомобилей — 1

Абсолютная частота для 110 автомобилей — 1

Абсолютная частота для 80 автомобилей — 1

Абсолютная частота для 105 автомобилей — 1

Абсолютная частота для 95 автомобилей — 1

Абсолютная частота для 85 автомобилей — 1

Пример 2: Рассмотрим выборку из 50 студентов и их оценок за экзамен. Подсчитаем абсолютную частоту оценок:

Оценка «Отлично» — 10 студентов

Оценка «Хорошо» — 20 студентов

Оценка «Удовлетворительно» — 15 студентов

Оценка «Неудовлетворительно» — 5 студентов

Теперь мы можем подсчитать абсолютную частоту для каждой оценки:

Абсолютная частота для оценки «Отлично» — 10

Абсолютная частота для оценки «Хорошо» — 20

Абсолютная частота для оценки «Удовлетворительно» — 15

Абсолютная частота для оценки «Неудовлетворительно» — 5

Это лишь некоторые примеры использования абсолютной частоты в математике. Она может быть применена для различных типов данных и в разных областях математики, статистики и исследований.

Абсолютная частота в графиках и диаграммах

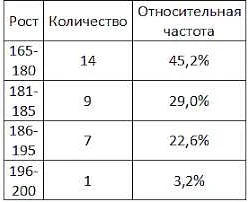
Абсолютная частота также может быть представлена в графическом виде с помощью различных типов графиков и диаграмм. Это позволяет наглядно представить данные и сравнить абсолютные частоты разных категорий или значений.

Одним из наиболее распространенных типов графиков для отображения абсолютной частоты является столбчатая диаграмма. На этой диаграмме каждая категория или значение представлена вертикальным столбцом, длина которого пропорциональна абсолютной частоте. Таким образом, сравнивая длины столбцов, можно сделать выводы о различиях в абсолютной частоте разных категорий или значений.

Круговая диаграмма также может быть использована для отображения абсолютной частоты. На круговой диаграмме каждая категория или значение представлена сектором, площадь которого пропорциональна абсолютной частоте. Таким образом, сравнивая площади секторов, можно сделать выводы о различиях в абсолютной частоте разных категорий или значений.

Графики и диаграммы, отображающие абсолютную частоту, могут быть полезными инструментами для визуализации данных и представления результатов исследований. Они позволяют наглядно представить информацию и сделать выводы на основе анализа абсолютных частот различных категорий или значений.

Абсолютная частота в математических моделях

В математических моделях абсолютная частота может быть полезной при определении вероятности наступления определенного события. Например, если провести серию экспериментов по бросанию кости и записать количество выпадения каждой грани, то можно использовать абсолютную частоту, чтобы определить вероятность выпадения каждого значения.

Абсолютная частота может быть представлена в виде списка или таблицы, где каждое значение сопровождается соответствующим количеством раз, которое оно встречается. Это позволяет наглядно представить распределение частот и провести анализ данных.

Примером абсолютной частоты в математических моделях может быть анализ результатов опроса. Если провести опрос среди группы людей и записать количество ответов на каждый вопрос, то можно использовать абсолютную частоту, чтобы определить наиболее популярные ответы или тенденции в ответах.

Абсолютная частота и относительная частота: разница

Абсолютная частота отражает количество раз, которое определенное значение встречается в наборе данных. Она показывает, сколько раз данное значение повторяется в выборке. Например, если мы имеем выборку из 100 человек и хотим узнать, сколько человек имеют рост 170 см, то абсолютная частота будет показывать, сколько раз значение «170» встречается в этой выборке.

Относительная частота, с другой стороны, показывает, какую долю составляет определенное значение от общего количества наблюдений. Она измеряется в процентах или долях и позволяет сравнить значения на основе их относительной величины. Например, если у нас есть выборка из 100 человек и 20 из них имеют рост 170 см, то относительная частота для значения «170» будет равна 20% или 0,2.

Таким образом, основная разница между абсолютной и относительной частотой заключается в их измерении и целях. Абсолютная частота показывает количество повторений конкретного значения, а относительная частота позволяет сравнивать значения на основе их доли в общем объеме данных. Оба этих показателя являются важными инструментами статистического анализа и помогают в анализе данных и выявлении закономерностей.

Значение абсолютной частоты в исследованиях и анализе данных

В исследованиях и анализе данных абсолютная частота играет важную роль. Она позволяет определить количество раз, которое определенное значение или событие встречается в наборе данных. Абсолютная частота помогает исследователям понять распределение данных и выделить наиболее значимые значения.

Значение абсолютной частоты особенно полезно при анализе качественных данных, таких как категориальные переменные. Например, при исследовании предпочтений потребителей можно использовать абсолютную частоту для определения самых популярных продуктов или услуг. Анализировать абсолютную частоту также можно для определения частоты появления определенных событий, например, в анализе нежелательных событий или аварий.

При проведении статистических исследований абсолютная частота может использоваться для определения частоты появления определенных значений в выборке или популяции. С помощью абсолютной частоты можно определить основные характеристики данных, такие как мода — значение с наибольшей абсолютной частотой, или медиана — значение, разделяющее набор данных на две равные части.

В исследованиях по социальным наукам абсолютная частота может использоваться для изучения распределения определенных характеристик в обществе. Например, исследователи могут использовать абсолютную частоту для определения распределения определенных демографических характеристик, таких как возраст, пол или образование, среди населения.

Итак, значение абсолютной частоты в исследованиях и анализе данных заключается в том, что она помогает определить количество раз, которое определенное значение или событие встречается в наборе данных. Это позволяет исследователям анализировать и понимать распределение данных, выделять наиболее значимые значения и проводить статистические выводы на основе этих данных.