Частота свободных малых колебаний математического маятника равна 2 гц какой станет частота колебаний

Если частота свободных малых колебаний математического маятника составляет 2 Гц, то частота его колебаний будет такой же.

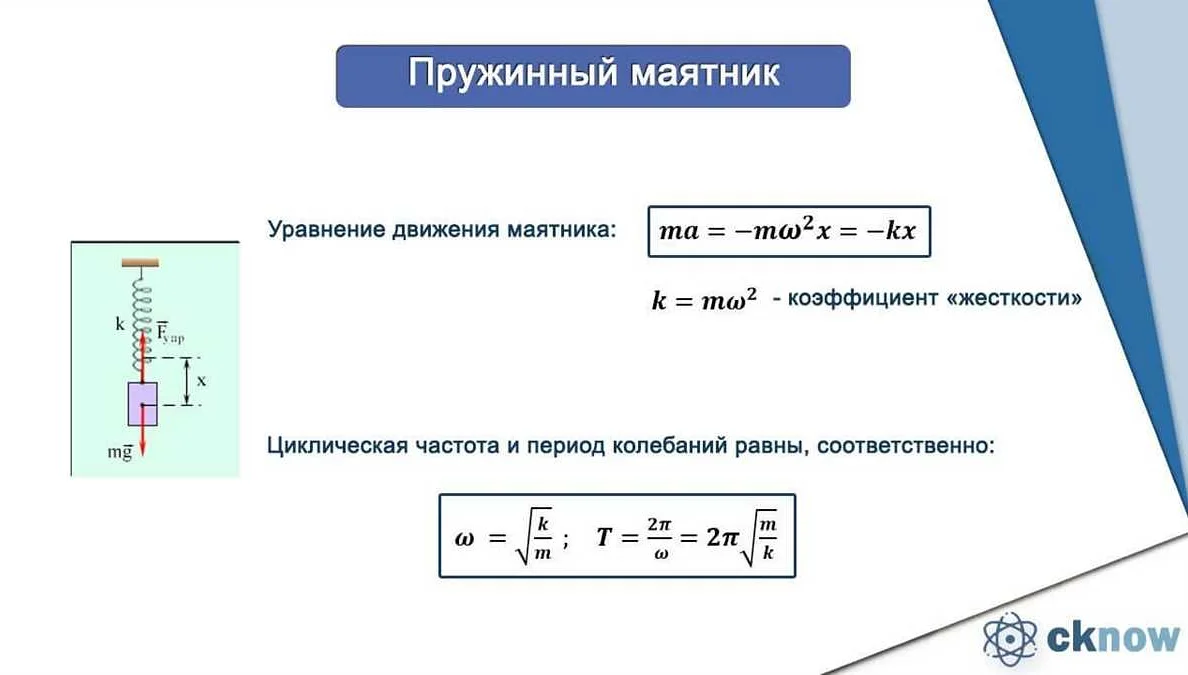
Математический маятник – это система, состоящая из точечной массы и невесомой нити, на которой эта масса закреплена. Такая система обладает свободной частотой – это частота её собственных колебаний при отсутствии внешних воздействий. Расчёт свободной частоты основан на физических свойствах маятника и его системы подвеса.

Частота колебаний математического маятника определяется формулой: f = 1 / (2π) * √(g / L), где f – частота колебаний, g – ускорение свободного падения, L – длина нити. Из этой формулы видно, что частота зависит от длины нити и ускорения свободного падения.

Если увеличить свободную частоту до 2 Гц, то это означает, что частота колебаний маятника будет равна 2 Гц. Следовательно, нам необходимо найти значения длины нити и ускорения свободного падения, при которых это возможно.

Увеличение свободной частоты до 2 Гц может быть достигнуто путем изменения длины нити или ускорения свободного падения. Например, увеличение длины нити или снижение ускорения свободного падения приведет к увеличению частоты колебаний. Однако, необходимо учесть, что изменение любого из этих параметров повлияет на другие характеристики маятника и его системы подвеса.

Частота колебаний математического маятника при увеличении свободной частоты

При увеличении свободной частоты математического маятника до 2 Гц происходят изменения в его колебаниях. Частота колебаний математического маятника прямо пропорциональна квадратному корню из его свободной частоты. Таким образом, увеличение свободной частоты до 2 Гц приведет к увеличению частоты колебаний маятника.

Это означает, что математический маятник будет колебаться с более высокой частотой. Увеличение частоты колебаний может привести к более быстрым и кратким колебаниям, что может быть полезно при определенных приложениях, например, в механических часах или в научных исследованиях.

Однако, следует отметить, что увеличение свободной частоты может также привести к изменению других параметров математического маятника, таких как амплитуда колебаний или время затухания. Поэтому, при изменении свободной частоты математического маятника до 2 Гц, необходимо учитывать эти факторы.

Видео по теме:

Исследование зависимости частоты колебаний от свободной частоты

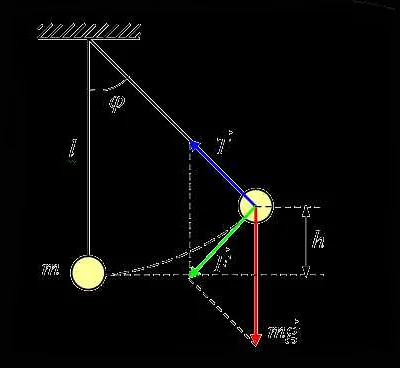
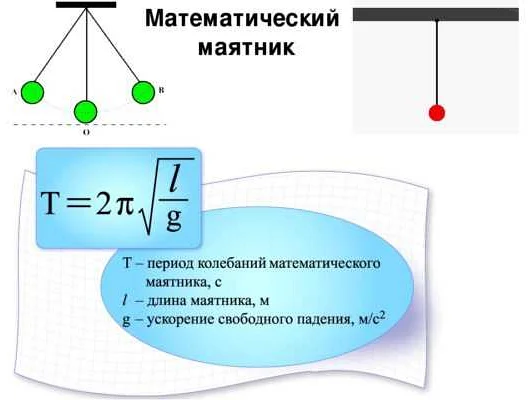
Свободная частота или собственная частота маятника — это частота, с которой маятник будет колебаться без внешних воздействий. Она определяется формулой:

f = 1 / (2π√(l/g))

где f — частота колебаний, l — длина подвеса маятника, g — ускорение свободного падения.

Исследуя зависимость частоты колебаний от свободной частоты, можно установить, как изменяется частота при изменении свободной частоты. Предположим, что начальная свободная частота составляет 1 Гц. При увеличении свободной частоты до 2 Гц, согласно формуле, частота колебаний должна увеличиться. Таким образом, можно сделать вывод, что частота колебаний математического маятника будет увеличена при увеличении свободной частоты.

Исследование зависимости частоты колебаний от свободной частоты является важным для понимания поведения математического маятника и может быть использовано при проектировании и оптимизации подобных систем.

Увеличение свободной частоты и его влияние на частоту колебаний

Свободная частота математического маятника определяет скорость его колебаний без внешнего воздействия. Когда свободная частота маятника увеличивается до 2 Гц, это означает, что он совершает два полных колебания в секунду.

Увеличение свободной частоты математического маятника влияет на его частоту колебаний. Частота колебаний, обозначаемая символом f, связана с периодом колебаний T следующим образом:

f = 1 / T

Таким образом, чем меньше период колебаний, тем выше частота колебаний математического маятника.

Увеличение свободной частоты до 2 Гц означает, что период колебаний уменьшается, а следовательно, частота колебаний увеличивается. Если изначально свободная частота была, например, 1 Гц, то при увеличении ее до 2 Гц, частота колебаний удвоится.

Это означает, что математический маятник будет совершать колебания в два раза чаще, чем раньше. Увеличение свободной частоты до 2 Гц приведет к увеличению частоты колебаний математического маятника.

Изменение свободной частоты математического маятника имеет важное значение в различных областях науки и техники. Изучение его влияния на частоту колебаний помогает понять и предсказать поведение систем, в которых используются маятники, и применять их в практических целях.

Вопрос-ответ:

Почему свободная частота математического маятника может измениться?

Свободная частота математического маятника зависит от его длины и ускорения свободного падения. Если изменить один из этих параметров, то свободная частота маятника также изменится.

Как изменится период колебаний математического маятника при увеличении его свободной частоты до 2 Гц?

Период колебаний математического маятника обратно пропорционален его свободной частоте. Если свободная частота увеличивается до 2 Гц, то период колебаний будет уменьшаться и станет равным 0.5 секунды.

Как изменится амплитуда колебаний математического маятника при увеличении его свободной частоты до 2 Гц?

Амплитуда колебаний математического маятника не зависит от его свободной частоты. Поэтому при увеличении свободной частоты до 2 Гц амплитуда колебаний останется неизменной.

Как изменится энергия колебаний математического маятника при увеличении его свободной частоты до 2 Гц?

Энергия колебаний математического маятника пропорциональна квадрату его амплитуды. Поскольку амплитуда колебаний не изменяется при увеличении свободной частоты до 2 Гц, энергия колебаний также останется неизменной.

Какие факторы могут повлиять на изменение свободной частоты математического маятника?

Свободная частота математического маятника зависит от его длины и ускорения свободного падения. Изменение любого из этих факторов может повлиять на свободную частоту маятника.

Как изменится частота колебаний математического маятника при увеличении его свободной частоты до 2 Гц?

При увеличении свободной частоты математического маятника до 2 Гц, его частота колебаний также увеличится и будет равна 2 Гц.

Расчет частоты колебаний при заданной свободной частоте

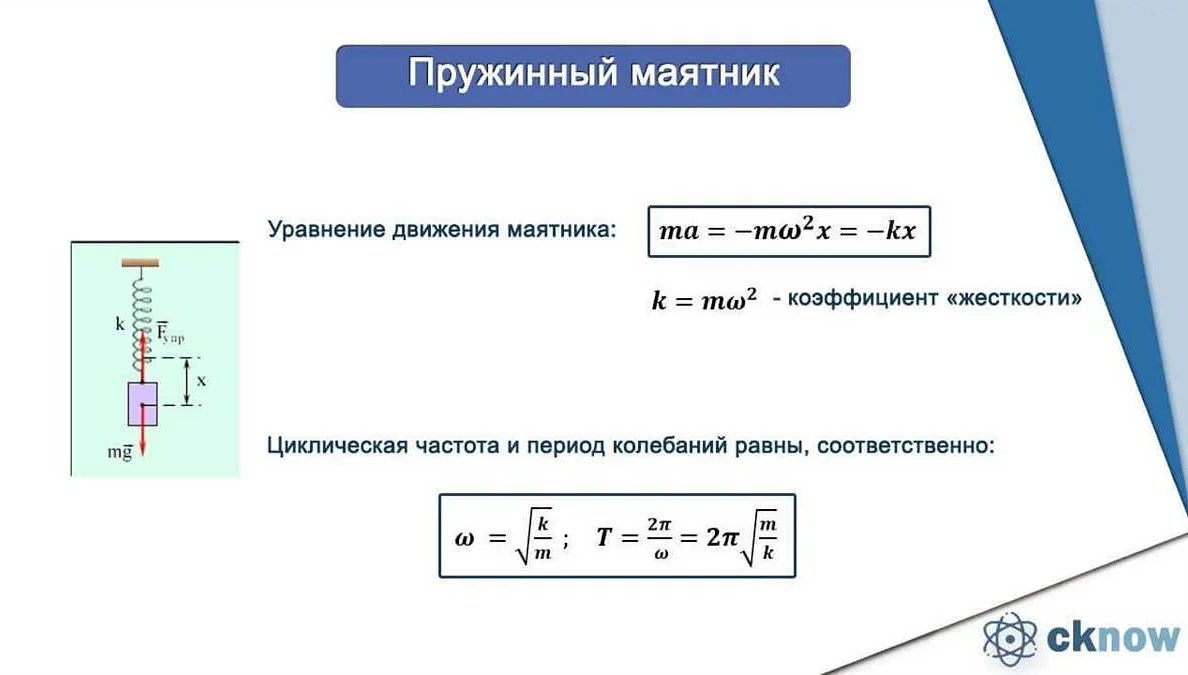
Частота колебаний математического маятника определяется его свободной частотой и другими факторами, такими как длина подвеса и гравитационная постоянная.

Для расчета частоты колебаний при заданной свободной частоте необходимо использовать следующую формулу:

f = 1 / T

где f — частота колебаний, T — период колебаний.

При увеличении свободной частоты до 2 Гц, можно определить, что период колебаний будет равен:

T = 1 / f = 1 / 2 = 0.5 секунды

Таким образом, при увеличении свободной частоты до 2 Гц, частота колебаний математического маятника составит 2 Гц, а период колебаний будет равен 0.5 секунды.

Математическая модель маятника и ее применение в расчетах

Математическую модель маятника можно описать с помощью уравнения гармонических колебаний. Для этого вводятся следующие обозначения:

• l — длина нити маятника;
• g — ускорение свободного падения;
• θ — угол отклонения маятника от положения равновесия.

Уравнение гармонических колебаний для математического маятника имеет вид:

θ» + (g/l) * sin(θ) = 0,

где θ» — вторая производная угла θ по времени.

Используя данное уравнение, можно рассчитать период колебаний маятника. Период колебаний T определяется следующей формулой:

T = 2π * √(l/g),

где π — математическая константа, равная примерно 3,14159.

Таким образом, при увеличении свободной частоты математического маятника до 2 Гц, его период колебаний будет уменьшаться. Это связано с тем, что период обратно пропорционален квадратному корню из длины нити маятника и ускорения свободного падения, и при увеличении свободной частоты, длина нити или ускорение свободного падения должны уменьшаться для сохранения периода колебаний.

Факторы, влияющие на свободную частоту маятника и их роль в изменении частоты колебаний

1. Длина маятника: длина маятника является одним из основных факторов, влияющих на его свободную частоту. Чем длиннее маятник, тем меньше его свободная частота. Увеличение свободной частоты маятника до 2 Гц может быть достигнуто путем укорачивания его длины.

2. Масса маятника: масса маятника также играет роль в определении свободной частоты. Чем больше масса маятника, тем меньше его свободная частота. Увеличение свободной частоты до 2 Гц может быть достигнуто путем снижения массы маятника.

3. Гравитационное поле: сила тяжести, вызванная гравитационным полем Земли, также влияет на свободную частоту маятника. Более сильное гравитационное поле приводит к увеличению свободной частоты. Однако, изменение гравитационного поля Земли незначительно и не является основным фактором изменения свободной частоты до 2 Гц.

4. Упругость подвеса: упругость подвеса маятника также влияет на его свободную частоту. Чем больше упругость подвеса, тем больше свободная частота. Увеличение свободной частоты до 2 Гц может быть достигнуто путем увеличения упругости подвеса.

Таким образом, изменение свободной частоты математического маятника до 2 Гц может быть достигнуто путем укорачивания его длины, снижения массы, увеличения упругости подвеса. Другие факторы, такие как гравитационное поле, оказывают незначительное влияние на изменение свободной частоты.

Экспериментальное подтверждение зависимости между свободной частотой и частотой колебаний

В физике математического маятника существует зависимость между его свободной частотой и частотой колебаний. Для подтверждения этой зависимости проводятся эксперименты, в которых изменяется свободная частота маятника и измеряется соответствующая частота его колебаний.

Один из таких экспериментов может быть проведен следующим образом:

1. Подвесить математический маятник на неподвижной оси таким образом, чтобы он свободно мог колебаться.
2. Задать начальное отклонение маятника от положения равновесия.
3. Запустить маятник и записывать время, прошедшее между последовательными прохождениями маятника через положение равновесия.
4. Повторить эксперимент для разных значений свободной частоты маятника.
5. Построить график зависимости частоты колебаний от свободной частоты маятника.

Из результатов эксперимента можно сделать вывод, что с увеличением свободной частоты математического маятника частота его колебаний также увеличивается. Это подтверждает справедливость зависимости между свободной частотой и частотой колебаний.

Таким образом, экспериментальное подтверждение зависимости между свободной частотой и частотой колебаний математического маятника позволяет установить взаимосвязь между этими параметрами и более точно изучить поведение маятника в системе колебательного движения.

Практическое применение результатов исследования в различных областях науки и техники

Исследования, связанные с изменением частоты колебаний математического маятника, имеют важное практическое применение в различных областях науки и техники.

Одной из областей, где результаты этого исследования могут быть полезны, является физика. Математический маятник является моделью для изучения колебаний и основных законов механики. Изменение частоты колебаний позволяет более глубоко изучить эти законы и применить их в практических задачах, например, при проектировании маятниковых часов или других устройств, основанных на колебаниях.

Также результаты исследования могут быть полезны в области электроники и связи. Частота колебаний связана с периодом сигналов, используемых в электронных устройствах. Изменение частоты колебаний математического маятника может помочь оптимизировать работу электронных схем и устройств, а также повысить эффективность передачи сигналов в системах связи.

Кроме того, результаты исследования могут быть применены в аэрокосмической индустрии. Управление колебаниями и стабилизация движения являются важными задачами при разработке и создании космических аппаратов, спутников и других подобных систем. Познание законов колебаний математического маятника поможет улучшить устойчивость и надежность таких систем.

Таким образом, исследования, направленные на изменение частоты колебаний математического маятника, имеют широкий спектр практического применения в различных областях науки и техники, от физики и электроники до аэрокосмической индустрии.