Координаты точки как ее аналитический эквивалент математика

Узнайте, что такое аналитические координаты точки и как они позволяют математикам описывать положение точки на плоскости. Узнайте, как расчет координат помогает в решении геометрических задач и визуализации математических объектов.

Аналитическое представление координат точки – одно из основных понятий в математике. Оно позволяет определить положение точки на плоскости или в пространстве с помощью числовых значений. Координаты задаются относительно выбранной системы координат, которая включает в себя оси и начало отсчета.

В двумерной геометрии, например, система координат состоит из двух перпендикулярных осей – горизонтальной (Ox) и вертикальной (Oy). Начало координат обозначается буквой O. Для определения положения точки на плоскости необходимо указать ее горизонтальную и вертикальную координаты, которые обозначаются соответственно x и y.

В трехмерной геометрии система координат состоит из трех взаимно перпендикулярных осей – Ox, Oy и Oz. В этом случае, чтобы определить положение точки в пространстве, необходимо указать ее горизонтальную, вертикальную и глубинную координаты, которые обозначаются соответственно x, y и z.

Аналитическое представление координат точки является важным инструментом в решении геометрических и физических задач. Оно позволяет проводить точные вычисления и определять расстояния между точками, углы наклона, площади фигур и многое другое. Использование координатной системы позволяет упростить математические модели и анализировать объекты в различных пространственных измерениях.

Что такое аналитическое представление?

Аналитическое представление в математике относится к способу описания точек в пространстве или на плоскости с помощью координат. Координаты точки представляют собой числовые значения, которые указывают на ее положение относительно определенных осей.

На плоскости для представления точек обычно используется декартова система координат, состоящая из двух перпендикулярных осей: горизонтальной оси x и вертикальной оси y. Координаты точки в этой системе записываются в виде упорядоченной пары чисел (x, y), где x — это значение по горизонтальной оси, а y — значение по вертикальной оси.

В трехмерном пространстве для представления точек используется трехмерная декартова система координат, состоящая из трех перпендикулярных осей: горизонтальной оси x, вертикальной оси y и оси z, которая направлена вверх. Координаты точки в трехмерной системе записываются в виде упорядоченной тройки чисел (x, y, z), где x — значение по горизонтальной оси, y — значение по вертикальной оси и z — значение по оси z.

Аналитическое представление точек позволяет осуществлять различные операции, такие как нахождение расстояния между точками, задание уравнений прямых и плоскостей, а также решение геометрических задач. Оно является основой для многих областей математики и находит применение в различных научных и инженерных дисциплинах.

Координаты точки в прямоугольной системе координат

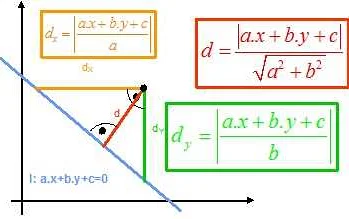
Каждая точка в прямоугольной системе координат имеет две координаты — абсциссу и ординату. Абсцисса точки определяет ее положение относительно горизонтальной оси, а ордината — относительно вертикальной оси.

Обозначение координат точки в прямоугольной системе координат происходит в виде упорядоченной пары чисел, где первое число — абсцисса точки, а второе число — ордината точки. Например, точка с координатами (3, 4) находится на расстоянии 3 единиц от начала горизонтальной оси и 4 единиц от начала вертикальной оси.

Координаты точек в прямоугольной системе координат могут быть положительными, отрицательными или нулевыми. Если абсцисса и ордината положительные, то точка находится в первой четверти плоскости. Если абсцисса положительная, а ордината отрицательная, то точка находится в четвертой четверти плоскости. Если абсцисса отрицательная, а ордината положительная, то точка находится во второй четверти плоскости. Если обе координаты отрицательные, то точка находится в третьей четверти плоскости. Если обе координаты равны нулю, точка находится в начале координат, которое обозначается символом O.

Координаты точки в полярной системе координат

В полярной системе координат положение точки определяется двумя величинами: радиусом и углом. Радиусом (r) измеряется расстояние от начала координат (полюса) до точки, а углом (θ) — направление от положительной оси до луча, проведенного из полюса до точки.

Таким образом, координаты точки в полярной системе представляются в виде упорядоченной пары (r, θ), где r — радиус, а θ — угол.

Радиус может быть любым положительным числом, а угол может принимать значения от 0 до 2π (или от 0 до 360 градусов), в зависимости от выбранной системы измерения углов.

Например, точка P с координатами (3, π/4) в полярной системе координат находится на расстоянии 3 от полюса и образует угол π/4 с положительной осью.

Использование полярной системы координат позволяет более удобно описывать положение точек в некоторых задачах, например, при описании движения объекта по окружности или при анализе полярных координатных графиков.

Преобразование координат между системами

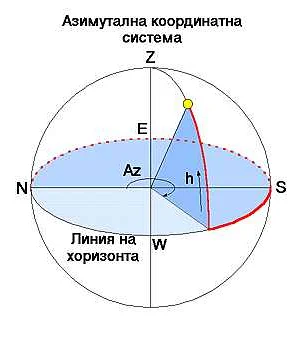
Существует несколько способов преобразования координат между системами, в зависимости от их структуры и особенностей. Наиболее распространенные из них:

1. Преобразование координат в декартовой системе в полярные или сферические координаты.
2. Преобразование координат в пространстве с помощью матриц поворота и смещения.
3. Преобразование координат в проекционных системах, таких как географические или картографические проекции.

Каждый из этих методов имеет свои особенности и применяется в различных областях науки и технологии. Например, преобразование в полярные координаты может быть полезным при описании движения объектов в полярных системах, таких как радары или антенны. Преобразование с помощью матриц поворота и смещения используется в компьютерной графике для перемещения и вращения объектов в трехмерном пространстве. Преобразование в проекционных системах позволяет отображать географические данные на плоскости карты или на экране компьютера.

Важно уметь выполнять преобразование координат между различными системами и понимать их математическую основу. Это позволяет более гибко работать с данными и использовать различные методы анализа и визуализации.

Операции над точками в прямоугольной системе координат

Операции над точками в прямоугольной системе координат включают:

Операция	Описание
Сложение	Суммирование координат точек. Результатом сложения двух точек (x1, y1) и (x2, y2) будет точка (x1 + x2, y1 + y2).
Вычитание	Вычитание координат точек. Результатом вычитания двух точек (x1, y1) и (x2, y2) будет точка (x1 — x2, y1 — y2).
Умножение на число	Умножение координат точки на число. Результатом умножения точки (x, y) на число a будет точка (a * x, a * y).
Деление на число	Деление координат точки на число. Результатом деления точки (x, y) на число a будет точка (x / a, y / a), при условии a ≠ 0.

Операции над точками позволяют выполнять различные манипуляции с координатами и получать новые точки в рамках прямоугольной системы координат.

Операции над точками в полярной системе координат

В полярной системе координат точка представляется в виде пары значений: радиуса и угла. Радиус указывает на расстояние от начала координат до точки, а угол определяет направление этого радиуса относительно положительного направления оси абсцисс.

Операции над точками в полярной системе координат включают сложение, вычитание, умножение и деление точек, а также нахождение расстояния между точками и нахождение координат точки, симметричной данной точке относительно начала координат.

1. Сложение точек

Сложение двух точек в полярной системе координат происходит путем сложения их радиусов и углов. Пусть имеются две точки A(r1, θ1) и B(r2, θ2). Тогда координаты точки C, полученной в результате сложения точек A и B, вычисляются по формулам:

r = r1 + r2

θ = θ1 + θ2

где r — радиус точки C, θ — угол точки C.

2. Вычитание точек

Вычитание точек в полярной системе координат аналогично сложению, только разность радиусов и углов. Пусть имеются две точки A(r1, θ1) и B(r2, θ2). Тогда координаты точки C, полученной в результате вычитания точки B из точки A, вычисляются по формулам:

r = r1 — r2

θ = θ1 — θ2

3. Умножение точки на число

Умножение точки в полярной системе координат на число происходит путем умножения радиуса точки на это число. Пусть имеется точка A(r, θ) и число k. Тогда координаты точки C, полученной в результате умножения точки A на число k, вычисляются по формулам:

r = k * r

θ = θ

4. Деление точки на число

Деление точки в полярной системе координат на число производится путем деления радиуса точки на это число. Пусть имеется точка A(r, θ) и число k. Тогда координаты точки C, полученной в результате деления точки A на число k, вычисляются по формулам:

r = r / k

θ = θ

5. Расстояние между точками

Расстояние между двумя точками в полярной системе координат вычисляется по формуле:

d = sqrt((r2 — r1)^2 + (θ2 — θ1)^2)

где d — расстояние между точками A и B.

6. Координаты симметричной точки

Координаты симметричной точки в полярной системе координат относительно начала координат вычисляются путем смены знака угла. Пусть имеется точка A(r, θ). Тогда координаты точки B, симметричной точке A относительно начала координат, вычисляются по формулам:

r = r

θ = -θ

Геометрическое представление точек на плоскости

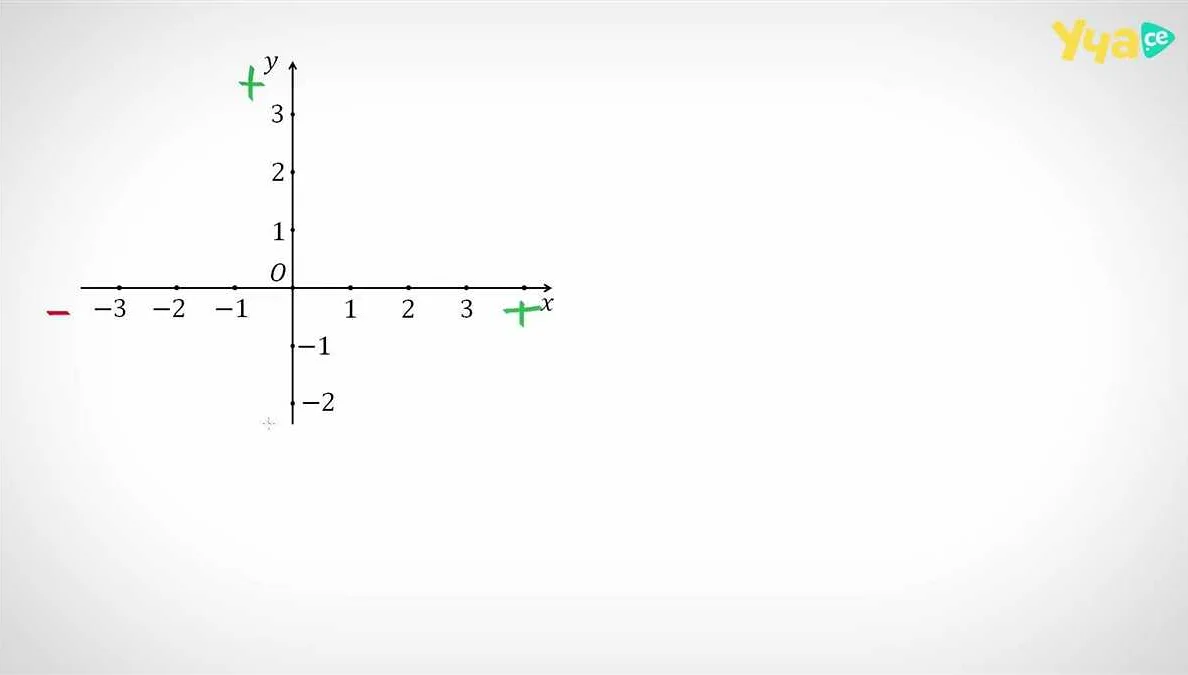
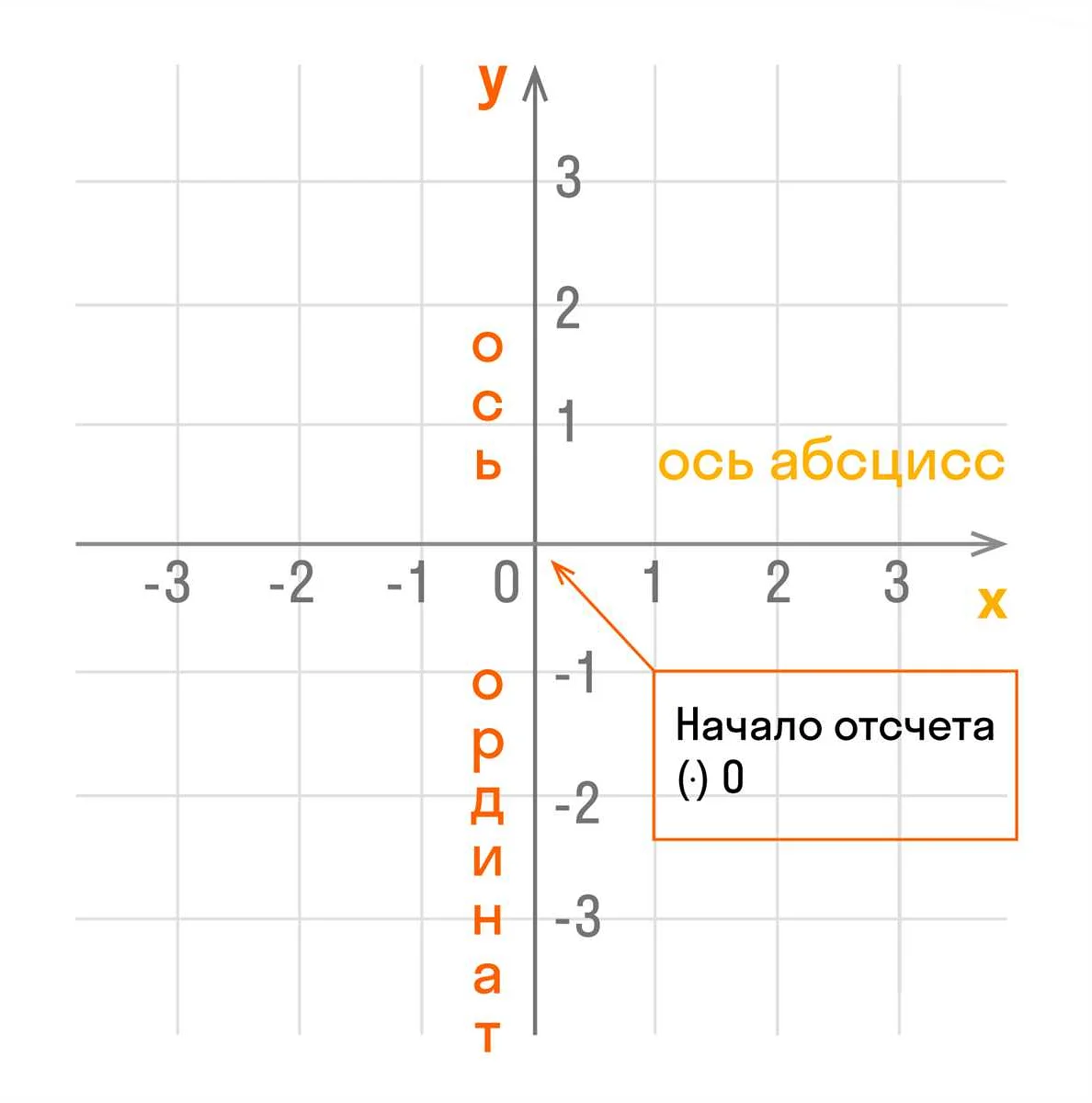
Координатная система является основой геометрического представления точек на плоскости. Она состоит из двух взаимно перпендикулярных прямых – осей координат. Одна ось называется горизонтальной (обычно обозначается осью OX) и отвечает за значение горизонтальной координаты точки. Другая ось называется вертикальной (обычно обозначается осью OY) и отвечает за значение вертикальной координаты точки. Точка пересечения осей координат называется началом координат и имеет координаты (0, 0).

Каждой точке на плоскости соответствуют две числовые величины – ее горизонтальная и вертикальная координаты. Горизонтальная координата измеряется вдоль оси OX, а вертикальная – вдоль оси OY. Обычно горизонтальную координату обозначают буквой x, а вертикальную – буквой y. Точка с координатами (x, y) на плоскости обозначает, что она находится x единиц от начала координат вдоль оси OX и y единиц от начала координат вдоль оси OY.

Геометрическое представление точек на плоскости позволяет проводить различные операции, такие как нахождение расстояния между точками, построение отрезков и прямых, определение углов и многое другое. Оно является основой для изучения геометрии и алгебры, а также находит применение в различных областях науки и техники.

Примеры использования аналитического представления

Аналитическое представление координат точки в математике находит широкое применение в различных областях и задачах. Ниже приведены несколько примеров использования аналитического представления:

1. Геометрия:

Аналитическое представление координат точки позволяет изучать и анализировать геометрические фигуры с помощью алгебраических методов. Например, для определения расстояния между двумя точками или угла между двумя векторами необходимо знать их координаты.

2. Физика:

В физике аналитическое представление используется для описания движения объектов, решения задач о силе и давлении, анализа электрических и магнитных полей и других физических величин. Например, при изучении движения тела в пространстве необходимо знать его координаты в зависимости от времени.

3. Экономика:

В экономике аналитическое представление координат используется для моделирования экономических процессов и анализа экономических данных. Например, при построении графиков спроса и предложения или при определении эластичности спроса и предложения необходимо знать координаты точек на графике.

4. Компьютерная графика:

В компьютерной графике аналитическое представление координат используется для создания и отображения графических объектов на экране. Например, при рисовании 2D и 3D графики необходимо знать координаты точек, линий и поверхностей, чтобы правильно отобразить изображение.

Это лишь некоторые из множества областей, где аналитическое представление координат точки находит применение. Знание и умение работать с аналитическим представлением является важным навыком для математиков, физиков, инженеров и других специалистов, работающих с числами и графиками.

Вопрос-ответ:

Что такое аналитическое представление координат точки?

Аналитическое представление координат точки — это способ записи координат точки на плоскости или в пространстве с помощью числовых значений, таких как числа на оси координат.

Какие системы координат используются в математике?

В математике используются разные системы координат, такие как декартова система координат, полярная система координат, цилиндрическая система координат и сферическая система координат.

Как записывается точка в декартовой системе координат?

В декартовой системе координат точка записывается в виде упорядоченной пары или упорядоченного тройки чисел, которые обозначают расстояние точки от начала координат по соответствующим осям.

Какие преимущества дает аналитическое представление координат точки?

Аналитическое представление координат точки позволяет легко определять расстояния между точками, находить середину отрезка, решать геометрические задачи с помощью алгебраических методов и проводить анализ графических данных.

Какие операции можно выполнять с координатами точек?

С координатами точек можно выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление. Это позволяет решать задачи на перемещение точек, нахождение расстояний и нахождение уравнений прямых и плоскостей.

Видео по теме: