Координаты это что в математике

Координаты в математике представляют собой числовые значения, которые определяют местоположение точки на плоскости или в пространстве. Они состоят из двух или трех чисел, соответствующих соответственно оси X, Y и, если нужно, оси Z. Использование координат позволяет точно указать положение объекта в пространстве и является основой для многих математических и физических концепций.

Координаты – одно из важнейших понятий в математике, которое позволяет определить положение точки в пространстве или на плоскости. С помощью координат можно описать местоположение объектов, решать геометрические задачи и анализировать данные. Для удобства обозначения координат в математике используются числовые значения.

В двумерном пространстве (плоскости) координаты точки задаются двумя числами – абсциссой и ординатой. Абсцисса обозначает расстояние точки от вертикальной оси, а ордината – расстояние точки от горизонтальной оси. Обозначение координат в двумерном пространстве обычно записывается в виде (x, y), где x – абсцисса, y – ордината.

В трехмерном пространстве координаты точки задаются тремя числами – абсциссой, ординатой и аппликатой. Абсцисса определяет расстояние точки от вертикальной оси, ордината – расстояние от горизонтальной оси, а аппликата – расстояние от горизонтальной плоскости. Обозначение координат в трехмерном пространстве записывается в виде (x, y, z), где x – абсцисса, y – ордината, z – аппликата.

Пример: рассмотрим точку A в двумерном пространстве с координатами (3, 2). Абсцисса этой точки равна 3, что означает, что она находится на расстоянии 3 единиц от вертикальной оси, а ордината равна 2, что означает, что точка находится на расстоянии 2 единиц от горизонтальной оси.

Определение координат в математике

В двумерной системе координат, также известной как плоскость, каждая точка может быть представлена парой чисел (x, y). Здесь x — это горизонтальная координата, а y — вертикальная координата. Начало координат обычно находится в центре плоскости и обозначается точкой (0, 0).

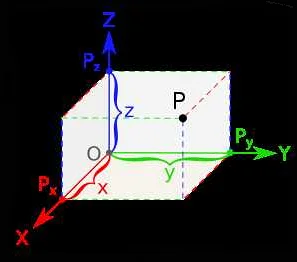
В трехмерной системе координат, каждая точка может быть представлена тройкой чисел (x, y, z). Здесь x — это горизонтальная координата, y — вертикальная координата, а z — глубина. Начало координат также находится в центре трехмерного пространства и обозначается точкой (0, 0, 0).

Координаты также могут быть представлены в виде дробных чисел или отрицательных чисел, чтобы указать точки, находящиеся за пределами основной системы координат.

Примеры использования координат

1. Географические координаты:

В географии координаты используются для определения точного местоположения на Земле. Широта и долгота являются основными географическими координатами. Например, город Москва находится приблизительно на координатах 55.7558° N (северной широты) и 37.6176° E (восточной долготы).

2. Координаты в декартовой системе:

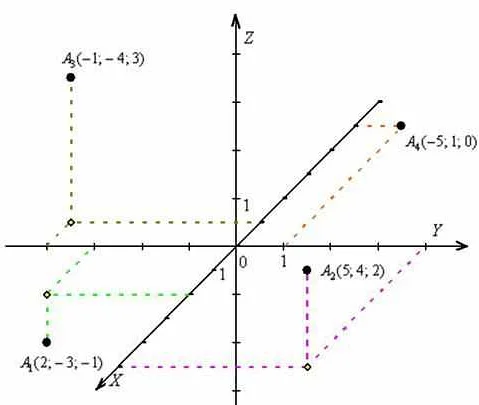
В математике и физике используется декартова система координат, в которой точка в пространстве определяется с помощью трех чисел (x, y, z). Например, точка A с координатами (2, 3, 4) находится на расстоянии 2 единицы по оси x, 3 единицы по оси y и 4 единицы по оси z.

3. Координаты в компьютерной графике:

В компьютерной графике координаты используются для определения положения пикселя на экране. Например, пиксель с координатами (100, 200) находится на 100 пикселей от левого края экрана и на 200 пикселей от верхнего края экрана.

4. Полярные координаты:

В полярной системе координат точка определяется с помощью расстояния от начала координат (радиус) и угла между положительным направлением оси x и линией, соединяющей начало координат с точкой. Например, точка B с полярными координатами (r, θ) имеет радиус r и угол θ относительно положительного направления оси x.

5. Координаты в топологии:

В топологии координаты используются для определения отношений между точками в пространстве. Например, в топологической сортировке графа каждой точке присваивается координата, отражающая ее порядок в сортировке.

Координатная плоскость и система координат

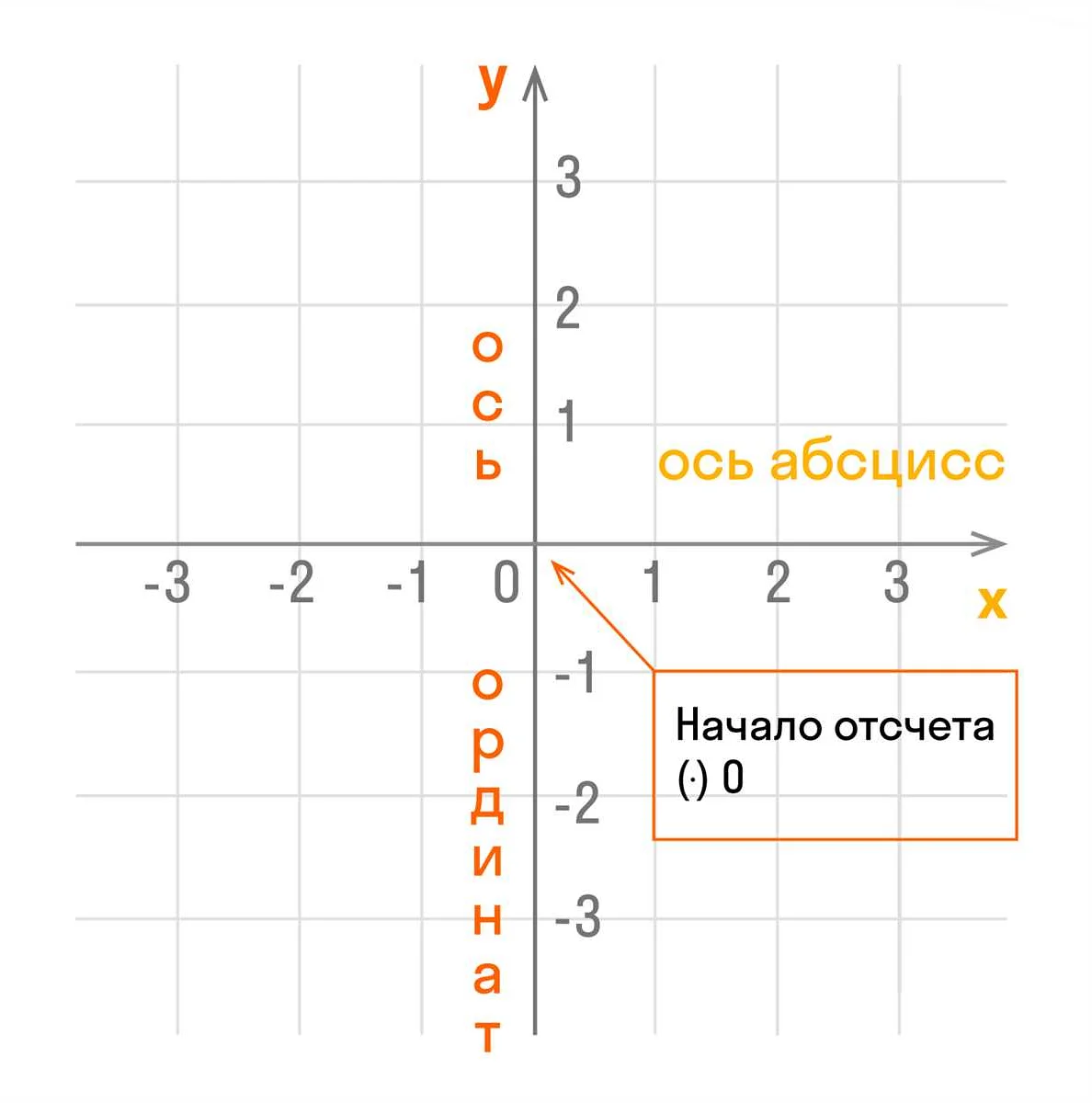
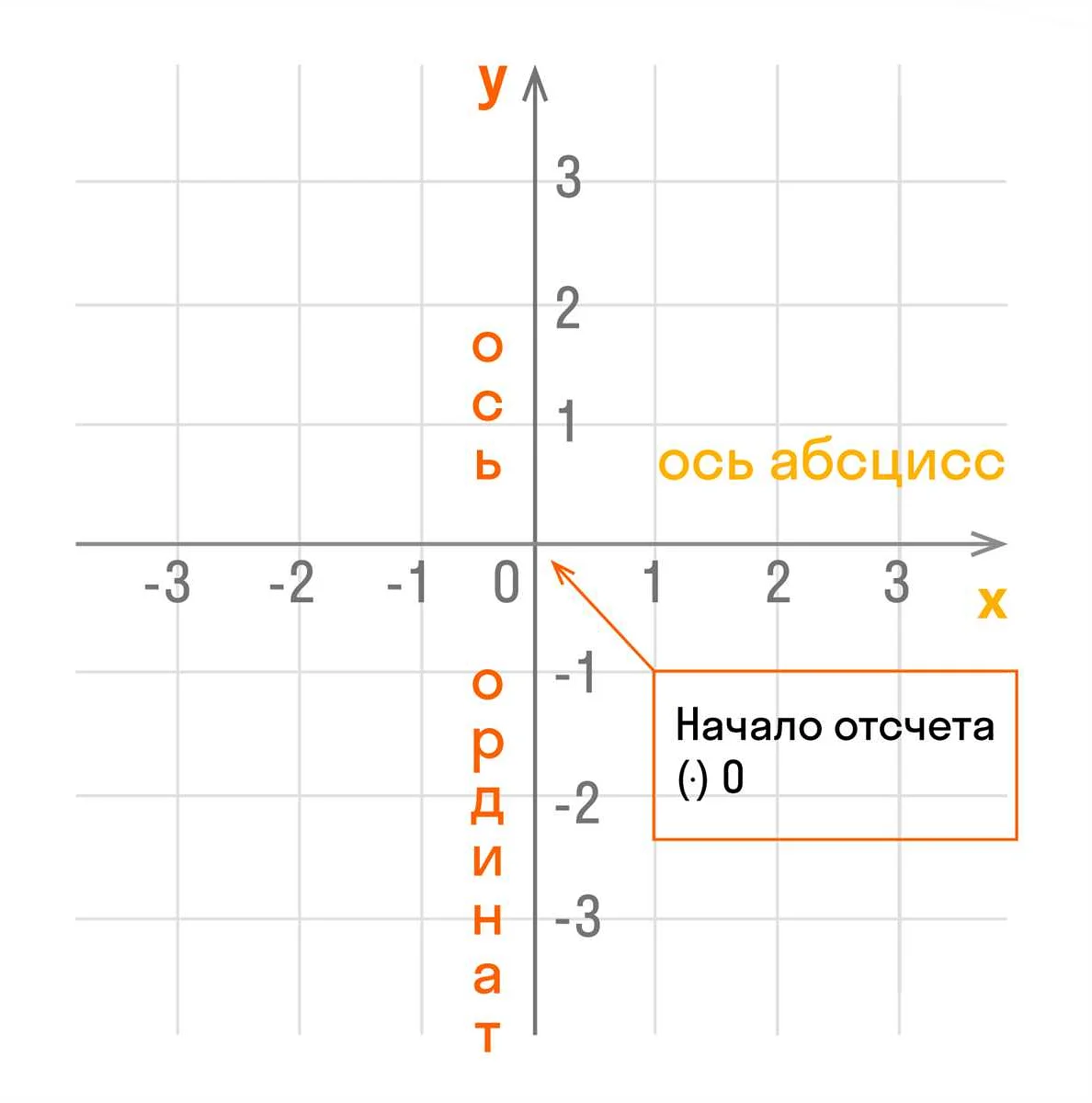
Система координат представляет собой набор правил и установок, с помощью которых можно описать положение точки на координатной плоскости. Она состоит из двух взаимно перпендикулярных осей – горизонтальной и вертикальной, которые называются осями абсцисс и ординат соответственно.

Ось абсцисс горизонтальна и простирается слева направо, образуя основу плоскости. Ось ординат вертикальна и простирается сверху вниз. Там, где оси пересекаются, находится начало координат, обозначаемое точкой O.

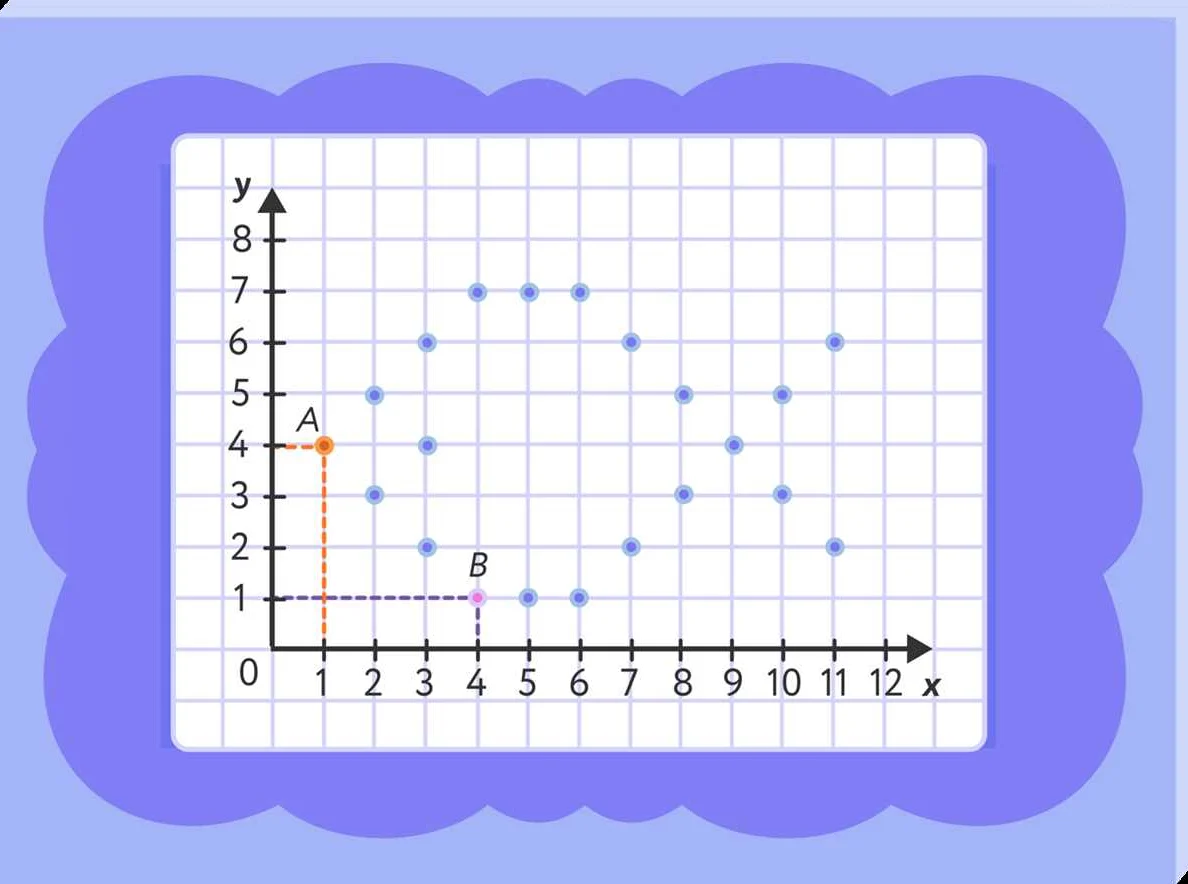
Каждая точка на координатной плоскости имеет свои координаты, которые записываются в виде пары чисел (x, y). При этом первое число в паре обозначает расстояние точки от начала координат по горизонтальной оси и называется абсциссой точки, а второе число обозначает расстояние точки от начала координат по вертикальной оси и называется ординатой точки.

Например, точка A с координатами (3, 4) находится на расстоянии 3 единиц от начала координат по оси абсцисс и на расстоянии 4 единиц по оси ординат. Точка B с координатами (-2, 1) находится на расстоянии 2 единиц от начала координат влево по оси абсцисс и на расстоянии 1 единицы вверх по оси ординат.

Прямоугольные координаты: x и y

В математике прямоугольные координаты используются для определения положения точки на плоскости. Каждая точка на плоскости имеет две координаты: x и y.

Координата x определяет расстояние точки от вертикальной оси, которая называется осью абсцисс. Если точка находится слева от начала координат, значение x будет отрицательным, а если справа — положительным.

Координата y определяет расстояние точки от горизонтальной оси, которая называется осью ординат. Если точка находится ниже начала координат, значение y будет отрицательным, а если выше — положительным.

Например, точка с координатами (3, 4) находится на расстоянии 3 от оси абсцисс (вправо) и 4 от оси ординат (вверх).

Точкаxy

A	2	-5
B	-1	3
C	0	0

В данной таблице приведены примеры точек с их прямоугольными координатами.

Полярные координаты: радиус и угол

Радиус определяет расстояние от начала координат до точки, а угол указывает направление точки от положительной полуоси x. Угол измеряется в градусах или радианах и может быть положительным или отрицательным.

Полярные координаты особенно полезны для описания точек, которые лежат на окружностях или других кривых, имеющих радиальную симметрию. Они также используются для удобного представления векторов, например, в физике или геометрии.

В полярных координатах точка обозначается в виде (r, θ), где r — радиус, а θ — угол. Например, точка с радиусом 3 и углом 45 градусов будет обозначаться как (3, 45°).

Если угол θ равен 0, то точка находится на положительной полуоси x. Если угол равен 90 градусам, то точка лежит на положительной полуоси y. Положительные углы отсчитываются против часовой стрелки, а отрицательные — по часовой стрелке.

Переход между полярными и декартовыми координатами осуществляется с помощью следующих формул:

x = r * cos(θ)

y = r * sin(θ)

где x и y — декартовы координаты, r — радиус, а θ — угол.

Координаты точек на графиках функций

Координаты точек на графике функции состоят из двух чисел: абсциссы и ординаты. Абсцисса точки определяет ее положение по горизонтальной оси, а ордината — по вертикальной оси.

Например, рассмотрим график функции y = x^2. Для этой функции координаты точек на графике можно найти, подставляя значения аргумента x в уравнение функции и вычисляя соответствующие значения y.

xy

-2	4
-1	1
0	0
1	1
2	4

Например, при x = -2, значение y будет равно 4. Это означает, что точка с координатами (-2, 4) будет находиться на графике функции y = x^2.

Использование координат точек на графиках функций позволяет анализировать и визуализировать свойства функций, а также находить решения уравнений и неравенств.

Географические координаты и GPS

Широта указывает на расстояние от данной точки до экватора и измеряется в градусах. Широта может быть северной или южной, в зависимости от того, находится ли точка выше или ниже экватора. Значение широты может варьироваться от -90° до 90°.

Долгота, с другой стороны, определяет положение точки на востоке или западе от Гринвича и также измеряется в градусах. Значение долготы может варьироваться от -180° до 180°.

GPS (Global Positioning System) – это навигационная система, которая использует сигналы, передаваемые спутниками, для определения точного местоположения на Земле. GPS основана на использовании географических координат и позволяет людям, транспорту и другим устройствам определять свое местоположение в реальном времени с высокой точностью.

Координаты, полученные с помощью GPS, широко используются в различных областях, таких как навигация, геодезия, туризм и многих других.

КоординатыМестоположение

55.7558° N, 37.6176° E	Москва, Россия
40.7128° N, 74.0060° W	Нью-Йорк, США
51.5074° N, 0.1278° W	Лондон, Великобритания

Вопрос-ответ:

Что такое координаты в математике?

Координаты в математике — это числа, которые позволяют определить положение точки на плоскости или в пространстве.

Какие виды координат существуют в математике?

Существует два основных вида координат: прямоугольные (декартовы) координаты и полярные координаты.

Как определить положение точки на плоскости с помощью прямоугольных координат?

Прямоугольные (декартовы) координаты состоят из двух чисел (x, y), где x — это расстояние точки от вертикальной оси (ось ординат), а y — это расстояние точки от горизонтальной оси (ось абсцисс).

Можете привести пример использования координат в математике?

Конечно! Например, в геометрии координаты используются для определения положения точек на плоскости или в пространстве. Они также могут использоваться в физике для описания движения тела или в экономике для построения графиков функций.

Как определить положение точки на плоскости с помощью полярных координат?

Полярные координаты состоят из двух чисел (r, θ), где r — это расстояние от начала координат до точки, а θ — это угол между положительным направлением оси абсцисс и линией, соединяющей начало координат и точку.

Что такое координаты в математике?

Координаты в математике — это числа, которые определяют положение точки на плоскости или в пространстве относительно некоторой фиксированной системы отсчета.

Координаты в компьютерной графике и моделировании

Координаты точек в компьютерной графике определяются относительно начала координатной системы, которое обычно находится в верхнем левом углу экрана. Каждая точка задается парой чисел (x, y), где x – горизонтальная координата, а y – вертикальная координата.

В трехмерной компьютерной графике используется трехмерная координатная система (x, y, z), где оси X и Y аналогичны двумерной системе, а ось Z указывает глубину или расстояние от экрана. Такая система координат позволяет создавать трехмерные объекты и эффекты, такие как перспектива, тени и текстуры.

Координаты в компьютерной графике и моделировании используются для рисования геометрических фигур, анимации, текстурирования, освещения и других визуальных эффектов. Они являются основой для работы с графическими программами, играми, виртуальной реальностью и компьютерной анимацией.

Видео по теме: