Что такое координата в математике
Содержимое
- 1 Что такое координата в математике
- 1.1 Координата: определение и значение в математике
- 1.2 Видео по теме:
- 1.3 Координатная прямая: основные понятия и свойства
- 1.4 Декартова система координат: основы и применение
- 1.5 Плоскость и трехмерное пространство: координатные системы
- 1.6 Координаты точки: как их определить и использовать
- 1.7 Примеры использования координат в геометрии
- 1.8 Координаты в физике: связь с пространственными понятиями
- 1.9 Вопрос-ответ:
- 1.9.0.1 Что такое координата в математике?
- 1.9.0.2 Какие примеры можно привести для понимания координат в математике?
- 1.9.0.3 Как можно задать координаты точки на плоскости?
- 1.9.0.4 Какие свойства имеют координаты точек на прямой?
- 1.9.0.5 Какие математические операции можно выполнять с координатами точек?
Координата в математике — это числовое значение, которое определяет положение точки на графике или в пространстве. Узнайте, какие виды координат существуют и как они используются в математических вычислениях.
Координата – это числовое значение, которое используется для определения положения точки, объекта или события в пространстве или на плоскости. В математике координаты широко применяются для описания геометрических фигур, решения уравнений и построения графиков.
Координатная система – это система абстрактных осей и плоскостей, которая используется для определения координат. В двумерной координатной системе точка определяется двумя числовыми значениями – абсциссой (x) и ординатой (y). Они образуют угол относительно оси x и позволяют точно указать местоположение объекта на плоскости.
Например, в координатной системе точка (2, 3) имеет абсциссу 2 и ординату 3. Это означает, что точка находится на расстоянии 2 единицы от начала координат по оси x и на 3 единицы от начала координат по оси y.
Координаты также широко применяются в трехмерной геометрии и физике. В трехмерной координатной системе точка определяется тремя числовыми значениями – абсциссой (x), ординатой (y) и аппликатой (z). Они позволяют точно указать положение объекта в пространстве.
Координата: определение и значение в математике
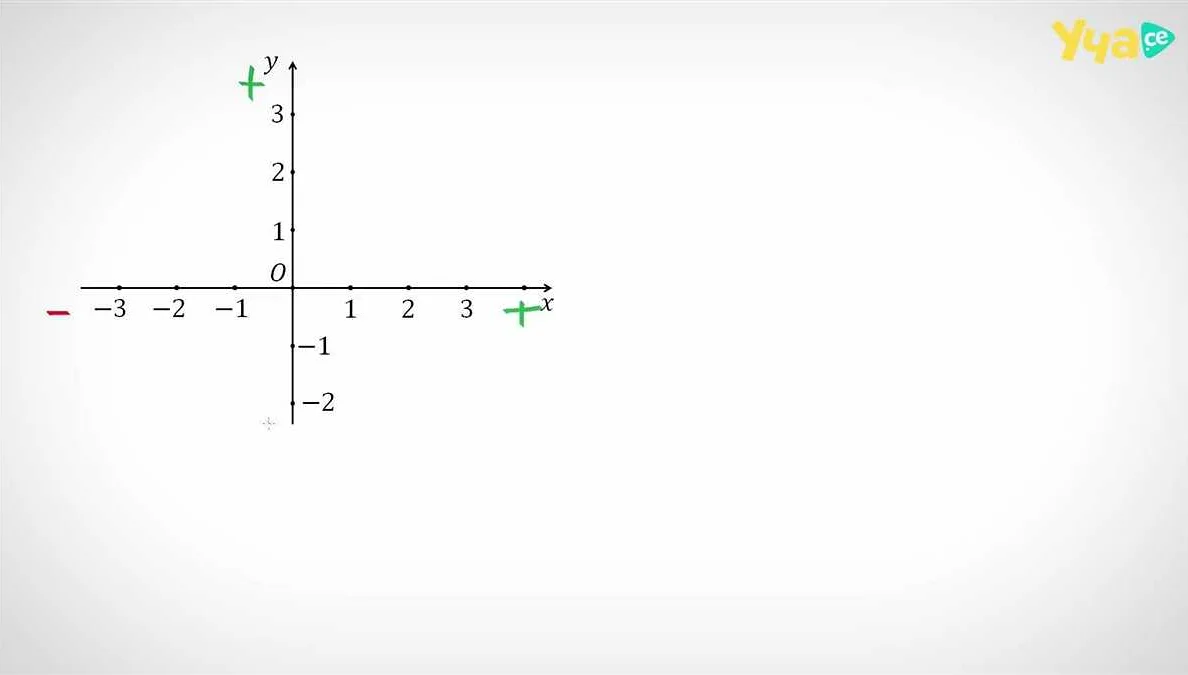
В двумерной геометрии координата состоит из двух чисел — абсциссы (x-координата) и ординаты (y-координата). Например, точка с координатами (3, 5) на плоскости расположена на расстоянии 3 единицы по горизонтали от начала координат и на 5 единиц по вертикали.
В трехмерной геометрии координата состоит из трех чисел — абсциссы (x-координата), ординаты (y-координата) и аппликаты (z-координата). Например, точка с координатами (2, 4, 6) в трехмерном пространстве расположена на расстоянии 2 единицы по горизонтали, 4 единицы по вертикали и 6 единиц по глубине.
Координаты в математике играют важную роль при решении геометрических задач, построении графиков функций, а также в других областях науки и техники. Они позволяют точно определить положение объектов и анализировать их свойства.
Видео по теме:
Координатная прямая: основные понятия и свойства
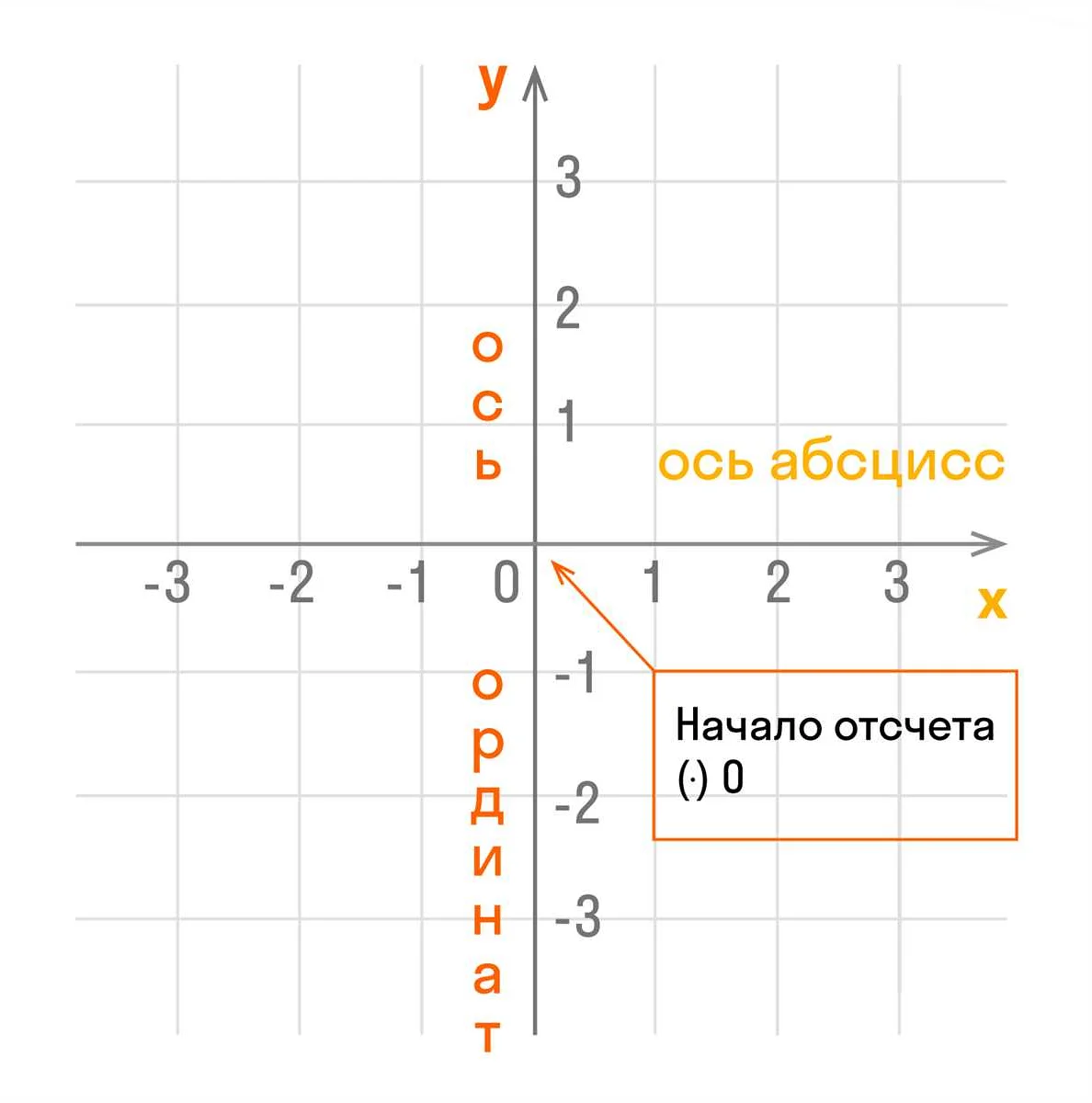
На координатной прямой существуют два направления: в положительную и отрицательную стороны. Обычно положительные значения координат находятся справа от начала отсчета, а отрицательные значения — слева. Начало координат, обозначаемое точкой O, находится в центре координатной прямой и имеет координату 0.
Координатная прямая делится на равные отрезки, которые называются делениями. Расстояние между двумя соседними делениями называется единицей измерения. Обычно на координатной прямой отмечаются основные деления, обозначаемые целыми числами. Также между основными делениями можно отмечать дополнительные деления, обозначаемые десятичными числами.
Свойства координатной прямой позволяют решать различные задачи и проводить различные операции. Например, с помощью координатной прямой можно находить расстояние между двумя точками, определять положение точки относительно других точек, строить отрезки и графики функций, решать уравнения и неравенства, а также многое другое.
Декартова система координат: основы и применение
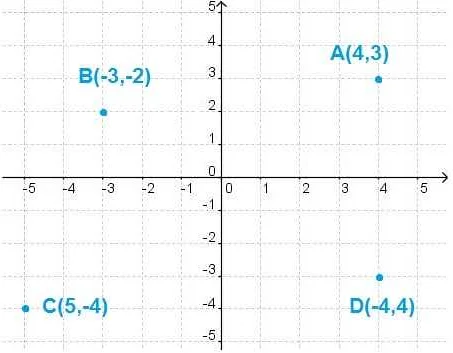
В декартовой системе координат пространство разбивается на две или три взаимно перпендикулярные оси. В двумерном случае это оси X и Y, а в трехмерном – оси X, Y и Z. Каждая ось имеет числовую шкалу, на которой указывается положение точки относительно начала координат.
Точка в декартовой системе координат задается упорядоченным набором чисел, называемых координатами. В двумерном случае это пара чисел (x, y), а в трехмерном – тройка чисел (x, y, z). Координата x указывает положение точки относительно оси X, координата y – относительно оси Y, а координата z – относительно оси Z.
Декартова система координат широко применяется в различных областях науки и техники. Например, она используется в геометрии для описания геометрических фигур и решения различных задач. Также она применяется в физике для описания положения и движения объектов в пространстве.
Основное преимущество декартовой системы координат заключается в ее простоте и удобстве использования. Она позволяет наглядно представить положение точек и взаимное расположение объектов. Благодаря этому, декартовая система координат является одной из основных математических концепций и языков для описания мира вокруг нас.
Плоскость и трехмерное пространство: координатные системы
На плоскости используется прямоугольная координатная система, которая состоит из двух перпендикулярных осей – горизонтальной (ось абсцисс) и вертикальной (ось ординат). Каждая точка плоскости имеет две координаты – абсциссу и ординату, которые обозначаются обычно буквами x и y соответственно. Например, точка A может быть описана координатами (3, 5), где 3 – абсцисса, а 5 – ордината.
В трехмерном пространстве используется прямоугольная декартова система координат, которая состоит из трех перпендикулярных осей – горизонтальной (ось x), вертикальной (ось y) и оси z, которая направлена вдоль высоты. Каждая точка трехмерного пространства имеет три координаты – x, y и z. Например, точка B может быть описана координатами (2, 4, -1), где 2 – координата по оси x, 4 – координата по оси y и -1 – координата по оси z.
Координатные системы на плоскости и в трехмерном пространстве позволяют решать широкий спектр задач, связанных с геометрией, физикой, инженерией и другими науками.
Координаты точки: как их определить и использовать
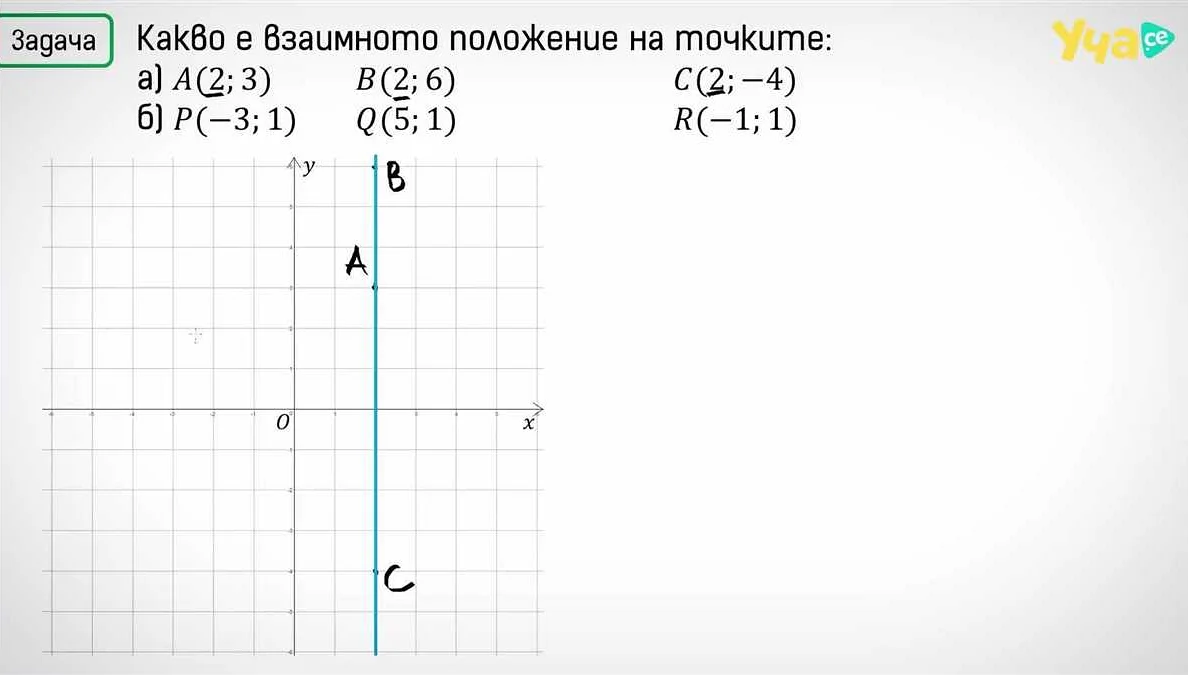
В математике координаты точки используются для ее определения на плоскости или в пространстве. Координаты представляют собой числа, которые указывают положение точки относительно определенных осей.
На плоскости используется система координат, состоящая из двух перпендикулярных осей — горизонтальной (ось абсцисс) и вертикальной (ось ординат). Точка на плоскости определяется двумя числами — ее абсциссой (x-координатой) и ординатой (y-координатой). Например, точка A с координатами (2, 3) находится на 2 единицы вправо от начала координат и на 3 единицы вверх.
В трехмерном пространстве используется система координат с тремя осями — осью x, осью y и осью z. Точка в пространстве определяется тремя числами — ее координатами x, y и z. Например, точка B с координатами (1, -2, 4) находится на 1 единицу вправо от начала координат, на 2 единицы вниз и на 4 единицы вперед.
Координаты точек могут использоваться для решения различных задач. Например, при построении графиков функций, определении расстояния между точками, нахождении площади фигур и т.д. Знание и понимание координат помогает анализировать и описывать геометрические объекты и их взаимное расположение.
Важно: при работе с координатами точек необходимо учитывать выбранную систему координат и правила ее использования. Ошибки в определении или использовании координат могут привести к неверным результатам и неправильному пониманию геометрических объектов.
В заключение, координаты точек — это числа, которые указывают положение точек относительно осей в системе координат. Они широко используются в математике и геометрии для определения и анализа геометрических объектов.
Примеры использования координат в геометрии
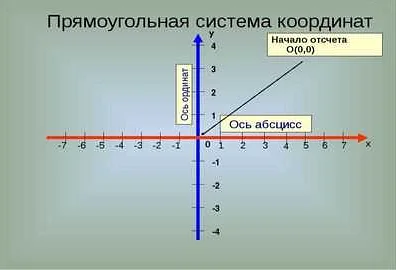
1. Плоскость координат: Для описания положения точек на плоскости используется система координат, состоящая из двух осей — горизонтальной (ось абсцисс) и вертикальной (ось ординат). Каждая точка на плоскости имеет уникальные координаты (x, y), где x — значение по оси абсцисс, а y — значение по оси ординат. Например, точка A с координатами (2, 3) на плоскости находится на расстоянии 2 единиц по оси абсцисс и 3 единицы по оси ординат от начала координат.
2. Векторы: Векторы также могут быть представлены в виде координат. Например, вектор AB может быть представлен как (x2-x1, y2-y1), где (x1, y1) — координаты начала вектора, а (x2, y2) — координаты конца вектора. Таким образом, координаты позволяют вычислить длину и направление вектора.
3. Геометрические фигуры: Координаты также используются для описания размеров и положения геометрических фигур, таких как прямоугольники, круги, треугольники и т.д. Например, прямоугольник может быть описан координатами двух противоположных углов (x1, y1) и (x2, y2).
4. Тригонометрия: В тригонометрии координаты используются для определения тригонометрических функций (синус, косинус, тангенс и т.д.) углов. Например, в прямоугольном треугольнике со сторонами a, b и гипотенузой c, синус угла α может быть определен как отношение координаты противолежащего катета к гипотенузе (sin α = a/c).
Координаты в физике: связь с пространственными понятиями
В физике координаты обычно используются в трехмерном пространстве, где каждая точка описывается тремя координатами: длиной, широтой и высотой. Эти координаты позволяют определить точное положение объекта в пространстве и его перемещение.
Координаты в физике также связаны с другими пространственными понятиями, такими как векторы и направления. Векторы могут быть использованы для описания перемещения объекта в пространстве, а направления могут помочь определить, куда направлена сила или движение.
Например, при описании движения тела в пространстве, координаты могут показать его положение в каждый момент времени, а векторы будут указывать направление и силу его движения.
Таким образом, координаты в физике играют важную роль в описании и изучении физических явлений и процессов, позволяя установить точное положение и перемещение объектов в пространстве и времени.
Вопрос-ответ:
Что такое координата в математике?
Координата в математике — это числовое значение, которое определяет позицию точки на прямой, плоскости или в пространстве. Она позволяет определить расстояние от точки до начала координатной системы. Координаты могут быть положительными, отрицательными или нулевыми в зависимости от их положения относительно начала координат.
Какие примеры можно привести для понимания координат в математике?
Один из примеров координат в математике — это прямая числовая ось. На этой оси каждой точке сопоставляется координата, которая является числовым значением позиции точки на оси. Например, точка с координатой 3 на числовой оси находится на расстоянии 3 единиц от начала координат, в положительную сторону. Другой пример — это координатная плоскость, где каждой точке сопоставляются две координаты: x-координата и y-координата.
Как можно задать координаты точки на плоскости?
Координаты точки на плоскости задаются парой чисел (x, y), где x — это горизонтальная координата, а y — вертикальная координата. Например, точка A с координатами (2, 4) находится на расстоянии 2 единиц вправо и 4 единиц вверх от начала координат.
Какие свойства имеют координаты точек на прямой?
На прямой координаты точек могут быть положительными, отрицательными или нулевыми, в зависимости от их положения относительно начала координат. Точка с положительной координатой находится в положительной полуплоскости, точка с отрицательной координатой находится в отрицательной полуплоскости, а точка с нулевой координатой находится в начале координат. Координаты точек также могут быть равными, если они находятся на одинаковом расстоянии от начала координат.
Какие математические операции можно выполнять с координатами точек?
С координатами точек можно выполнять различные математические операции, такие как сложение, вычитание, умножение и деление. Например, если даны две точки с координатами (x1, y1) и (x2, y2), то их координаты можно сложить для получения новой точки с координатами (x1 + x2, y1 + y2). Также можно находить расстояние между точками на основе их координат с помощью формулы расстояния между двумя точками в пространстве.
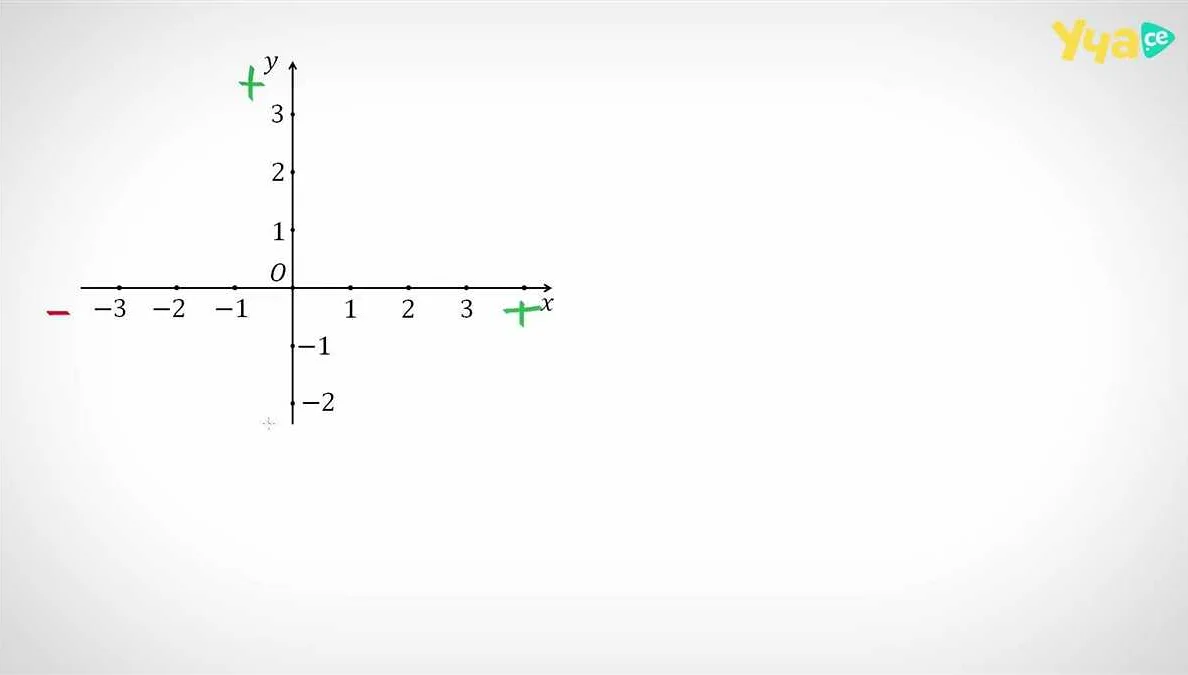

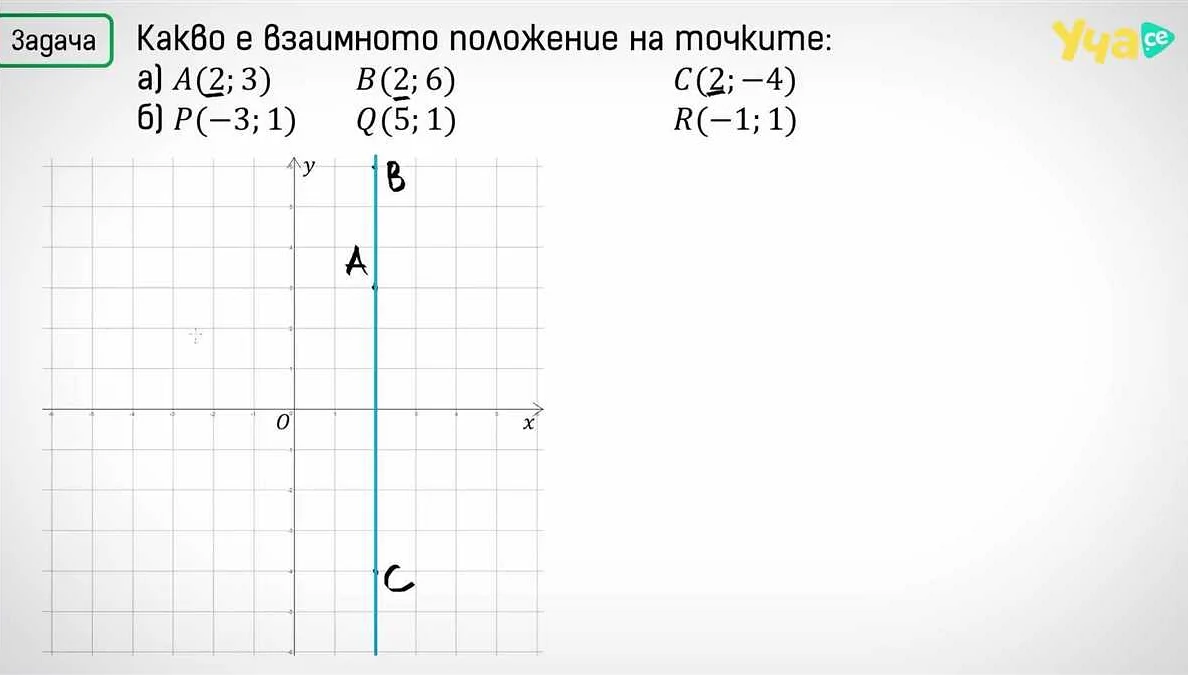

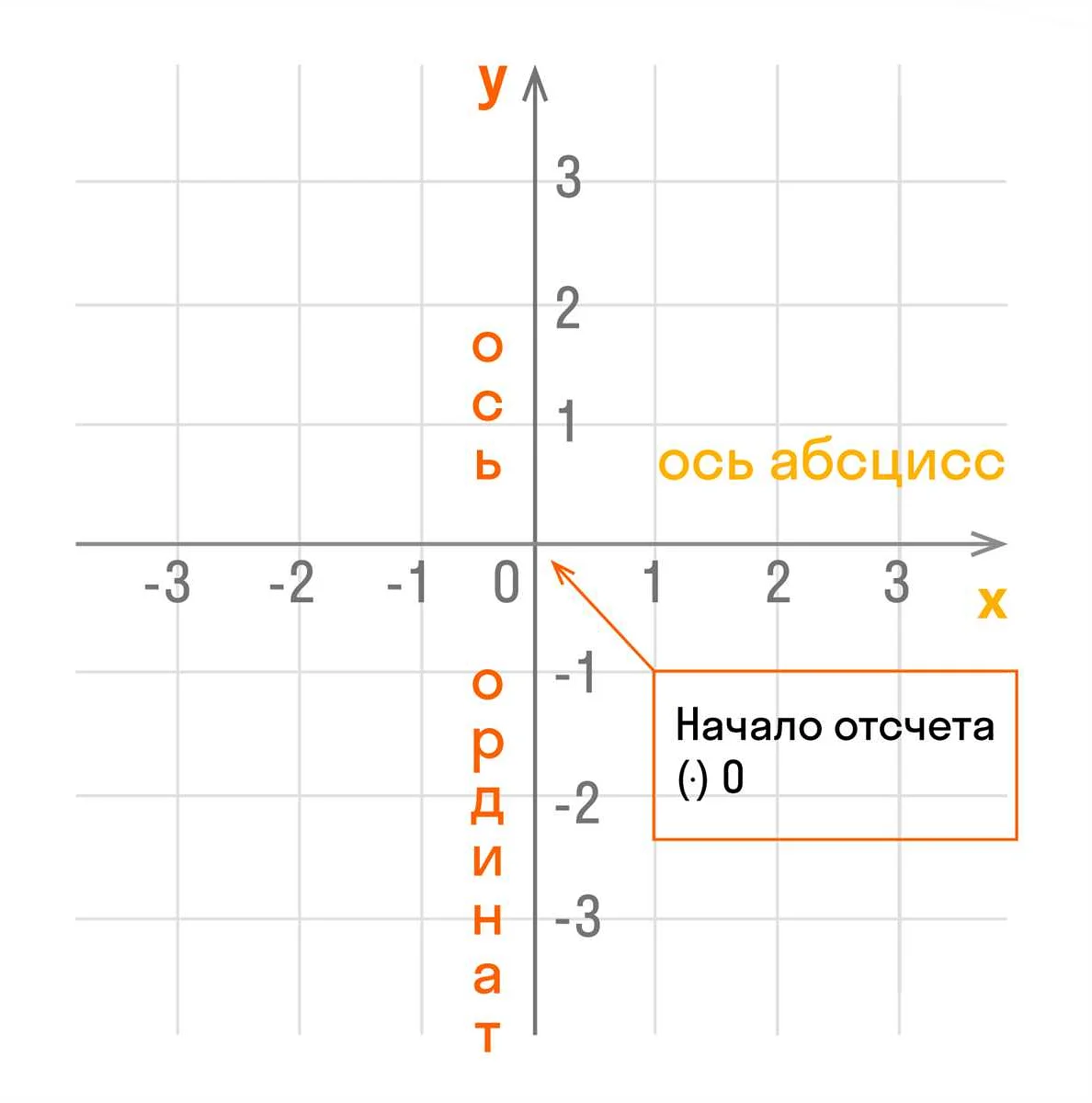
Координата в математике — это числовое значение, которое указывает на положение точки на плоскости или в пространстве. Она состоит из двух или более чисел, которые обозначают расстояние до осей координат. Координаты широко используются в геометрии, физике, экономике и других науках. Например, в двумерной плоскости координаты точки А могут быть (3, 5), где первое число указывает на расстояние до оси X, а второе — до оси Y. В трехмерном пространстве координаты могут быть (2, 3, 4), где первое число обозначает расстояние до оси X, второе — до оси Y и третье — до оси Z. Определение координат позволяет точно определить положение объектов и решать сложные задачи в различных областях науки и техники.
Координаты в математике — это числа, которые указывают положение точки на плоскости или в пространстве. Они используются для определения расстояния и направления относительно других точек. Каждая координата представляет собой числовое значение, которое определяет положение точки на оси. Например, на плоскости для точки А с координатами (3, 4) первое число 3 указывает положение точки по оси Х, а второе число 4 — по оси У. Таким образом, координаты помогают нам точно определить положение объекта в пространстве и использовать их для решения различных математических задач.
Очень интересная статья! Я всегда задумывалась, что такое координата в математике, и наконец-то получила ясное определение. Теперь понятно, что координата — это числовое значение, которое определяет положение точки относительно начала координат. Примеры с графиками очень помогли визуализировать эту концепцию. Теперь я смогу легко разобраться с системой координат и использовать ее в решении задач. Спасибо за разъяснения!
Координата – это числовое значение, которое задает позицию точки на плоскости или в пространстве. Определение координаты существенно упрощает решение математических задач и позволяет более точно описывать положение объектов. Например, в двумерной системе координат (x, y) каждая точка имеет две координаты – абсциссу (x) и ординату (y). Зная эти значения, мы можем определить точку на плоскости и провести с ней различные операции. В трехмерной системе координат (x, y, z) добавляется еще одна координата – глубина (z), что позволяет описывать положение точки в пространстве. Координаты находят применение в различных областях, включая геометрию, физику, информатику и географию. Изучение координат помогает улучшить понимание пространственных отношений и решать задачи более эффективно.