Что значит целые числа в математике 6 класс

Целые числа в математике для 6 класса — это набор чисел, включающий положительные и отрицательные числа, а также ноль. В статье вы узнаете, как работать с целыми числами, выполнять операции сложения, вычитания, умножения и деления, а также решать примеры и задачи на эту тему.

Целые числа являются одной из основных составляющих математической системы и являются расширением натуральных чисел. Они представляют собой числа, которые могут быть положительными, отрицательными или нулем. В шестом классе ученики впервые знакомятся с этими числами и изучают их основные свойства.

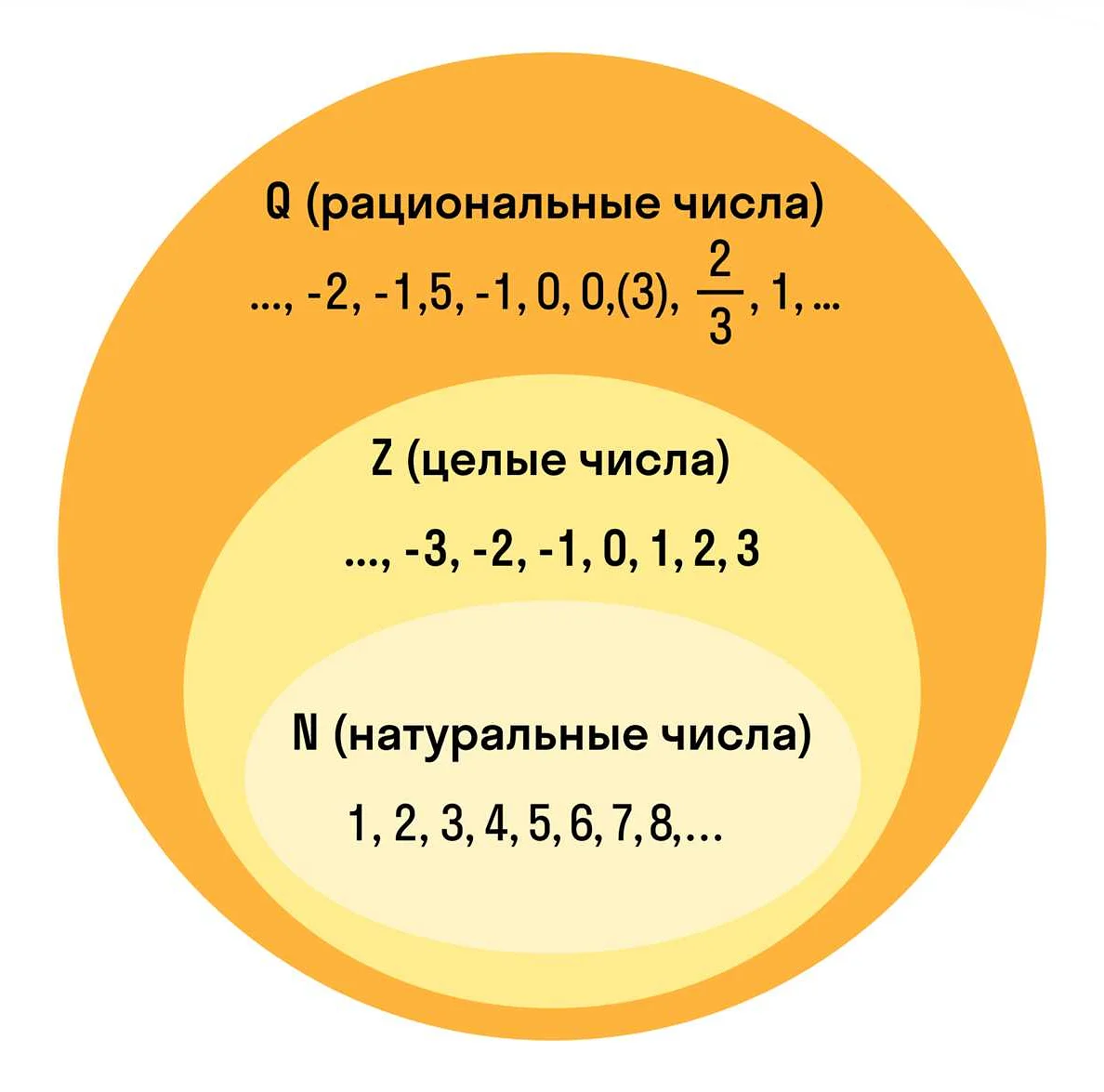
Определение целых чисел включает в себя все натуральные числа, их противоположности, а также нуль. Они обозначаются символом Z и записываются в виде {…, -3, -2, -1, 0, 1, 2, 3, …}. Целые числа можно представить на числовой прямой, где положительные числа расположены справа от нуля, отрицательные числа — слева, а ноль находится в центре.

Свойства целых чисел:

1. Сложение целых чисел: при сложении целых чисел с одинаковыми знаками, складываем их модули и ставим знак суммы. При сложении чисел с разными знаками, вычитаем из большего по модулю числа меньшее и ставим знак числа с большим модулем.

2. Умножение целых чисел: при умножении целых чисел с одинаковыми знаками получаем положительное число, а при умножении чисел с разными знаками — отрицательное число.

Что такое целые числа?

Целые числа включают в себя все натуральные числа, а также их отрицательные значения и ноль. Натуральные числа — это числа, которые используются для счета предметов или перечисления. Например, 1, 2, 3, 4, и так далее.

Значки «+», «-» и «0» используются для обозначения положительных, отрицательных и нулевых чисел соответственно. Например, +5, -10, 0.

Целые числа могут быть использованы для решения различных математических задач и применяются в различных областях науки и техники. Например, в физике, экономике, компьютерных науках и других.

Свойства целых чисел включают ассоциативность сложения и умножения, коммутативность сложения и умножения, существование нейтрального элемента относительно сложения и умножения, а также законы дистрибутивности и интервалы на числовой прямой.

ОбозначениеОписание

Z	Множество всех целых чисел
+	Сложение целых чисел
—	Вычитание целых чисел
*	Умножение целых чисел
0	Нейтральный элемент относительно сложения и умножения

Видео по теме:

Целые числа на числовой прямой

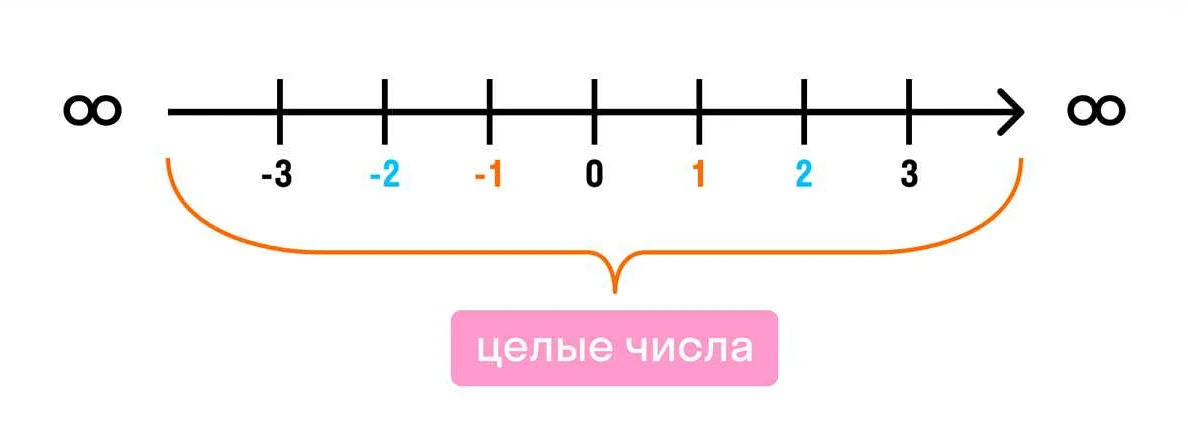
Целые числа представляют собой числовую систему, которая включает в себя все натуральные числа, их противоположности (отрицательные числа) и ноль. Для наглядного представления целых чисел используется числовая прямая, на которой числа располагаются в порядке возрастания или убывания.

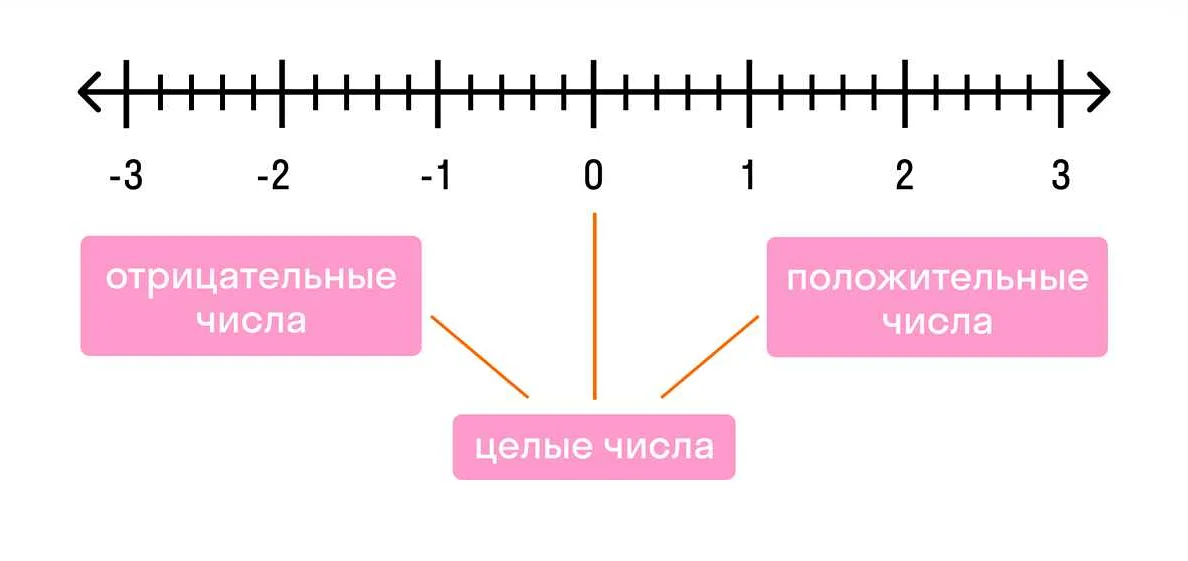
На числовой прямой положительные целые числа располагаются справа от нуля, а отрицательные — слева. Ноль занимает центральное положение и является нейтральным элементом.

Числовая прямая позволяет наглядно представить отношение между целыми числами и увидеть их взаимное расположение. Например, если на числовой прямой отметить число 2 и число -3, то можно сразу увидеть, что число -3 меньше числа 2, так как оно находится левее на прямой.

Целые числа на числовой прямой можно складывать и вычитать. Сложение целых чисел соответствует перемещению на число шагов вправо или влево на числовой прямой, а вычитание — на число шагов влево или вправо соответственно. Например, если на числовой прямой находится число 4, то при сложении с числом -2 мы перемещаемся на два шага влево и приходим к числу 2.

Таким образом, использование числовой прямой помогает визуализировать и понять основные свойства и операции с целыми числами.

Операции с целыми числами

Целые числа можно складывать, вычитать, умножать и делить. Все эти операции имеют свои правила и свойства.

Сложение целых чисел

Сложение целых чисел производится следующим образом: прибавляемое число (слагаемое) сначала ставим по оси чисел, а затем прибавляем к нему число, равное слагаемому. Если слагаемое положительное, то двигаемся вправо, если отрицательное – влево. Сумма будет располагаться на полученной позиции.

Вычитание целых чисел

Вычитание целых чисел можно представить как сложение с обратным числом. Для этого нужно взять обратное число вычитаемого и сложить его с уменьшаемым. Таким образом, вычитание сводится к сложению.

Умножение целых чисел

Умножение целых чисел производится по следующим правилам:

• Умножение на ноль дает ноль: 0 х а = 0.
• При умножении чисел одного знака получается положительное число: а х b > 0, если а и b одновременно положительны или отрицательны.
• При умножении чисел разного знака получается отрицательное число: а х b < 0, если а и b разных знаков.

Деление целых чисел

Деление целых чисел производится по следующим правилам:

• Деление на ноль невозможно.
• При делении числа на себя получается единица: а / а = 1.
• При делении числа на единицу результат равен самому числу: а / 1 = а.
• При делении числа на -1 результат равен числу с противоположным знаком: а / -1 = -а.

Свойства целых чисел при сложении

Сложение целых чисел имеет несколько основных свойств:

1. Сложение целых чисел ассоциативно. Это означает, что порядок складываемых чисел не меняет их суммы. Например: (а + b) + c = а + (b + c).
2. Сложение целых чисел коммутативно. Это означает, что порядок складываемых чисел не влияет на их сумму. Например: а + b = b + a.
3. Существует нейтральный элемент относительно сложения целых чисел. Это число 0. При сложении числа с нулем, получается исходное число. Например: а + 0 = а.
4. Для каждого целого числа а существует обратное число (-а), такое что а + (-а) = 0.

Эти свойства позволяют упрощать выражения и выполнять операции со сложением целых чисел более эффективно.

Свойства целых чисел при вычитании

Свойство 1: Коммутативность

При вычитании целых чисел порядок слагаемых можно менять местами без изменения результата. Например, для любых целых чисел a и b, a — b = b — a.

Свойство 2: Ассоциативность

При вычитании целых чисел можно изменять порядок выполнения операций без изменения результата. Например, для любых целых чисел a, b и c, (a — b) — c = a — (b — c).

Свойство 3: Существование обратного элемента

У каждого целого числа a существует обратное число (-a), такое что a + (-a) = 0.

Свойство 4: Аддитивность

При вычитании целых чисел можно разбивать сложные выражения на простые и вычислять результат для каждой части отдельно. Например, для любых целых чисел a, b и c, (a + b) — c = (a — c) + (b — c).

Эти свойства позволяют упростить вычисления и проводить преобразования с выражениями, содержащими вычитание целых чисел.

Свойства целых чисел при умножении

Умножение имеет свои особенности и свойства, которые помогают нам упростить вычисления и делать определенные заключения. Ниже приведены основные свойства целых чисел при умножении:

СвойствоОписаниеПример

Коммутативность	Порядок множителей не влияет на результат умножения.	3 * 4 = 4 * 3 = 12
Ассоциативность	Множители можно перегруппировывать без изменения результата.	(2 * 3) * 4 = 2 * (3 * 4) = 24
Распределительное свойство	Умножение можно распределить на сложение и вычитание.	3 * (2 + 4) = (3 * 2) + (3 * 4) = 18
Умножение на 0	Умножение на ноль всегда даёт ноль.	5 * 0 = 0
Умножение на 1	Умножение на единицу не меняет число.	7 * 1 = 7

Знание этих свойств помогает нам более эффективно работать с целыми числами и делать вычисления более простыми и понятными.

Свойства целых чисел при делении

Целые числа обладают несколькими важными свойствами при делении:

1. Если целое число делится нацело на другое целое число, то результатом деления также будет целое число. Например, 10 делится нацело на 5, поэтому результатом будет 2.
2. Если целое число делится нацело на себя, то результатом будет 1. Например, 20 делится нацело на 20, поэтому результатом будет 1.
3. Если целое число делится нацело на 1, то результатом будет само это число. Например, 15 делится нацело на 1, поэтому результатом будет 15.
4. Если целое число делится нацело на -1, то результатом будет противоположное число. Например, 12 делится нацело на -1, поэтому результатом будет -12.
5. Если целое число делится нацело на другое целое число, то остаток от деления будет также целым числом. Например, при делении 10 на 3, остаток будет равен 1.

Эти свойства целых чисел при делении являются основополагающими в математике и широко используются в различных областях науки и техники.

Вопрос-ответ:

Что такое целые числа?

Целые числа – это числа, которые являются результатом сложения или вычитания натуральных чисел. Они могут быть положительными, отрицательными или нулем.

Как можно представить целые числа на числовой прямой?

Целые числа можно представить на числовой прямой, где положительные числа располагаются справа от нуля, отрицательные – слева от нуля, а ноль находится точно в центре.

Как складывать и вычитать целые числа?

Для сложения целых чисел нужно сложить их абсолютные значения и сохранить знак числа с большим абсолютным значением. Для вычитания нужно придумать обратное число и применить правила сложения.

Какое свойство имеют целые числа при сложении?

Свойство целых чисел при сложении заключается в том, что сумма двух любых целых чисел всегда является целым числом.

Какое свойство имеют целые числа при умножении?

Свойство целых чисел при умножении заключается в том, что произведение двух любых целых чисел всегда является целым числом.

Что такое целые числа?

Целые числа — это числа, которые включают в себя натуральные числа, их отрицательные значения и ноль. Натуральные числа — это числа, которые используются для подсчета предметов или людей. Отрицательные числа обозначаются знаком минус перед числом и используются для обозначения долгов, отрицательных изменений или отрицательных величин.