В чем различия между нодом и ноком в математике для учеников 6 класса?

Различия между нодом и ноком в математике 6 класса. Узнайте, как эти понятия отличаются и как их использовать в решении задач. Научитесь правильно применять нод и нок в математических операциях и расчетах.

Нод и нок – два понятия, которые встречаются в математике и активно используются при решении задач на числа и их свойства в 6 классе. Хотя оба термина относятся к нахождению общих делителей или кратных чисел, они имеют различные значения и применяются в разных ситуациях.

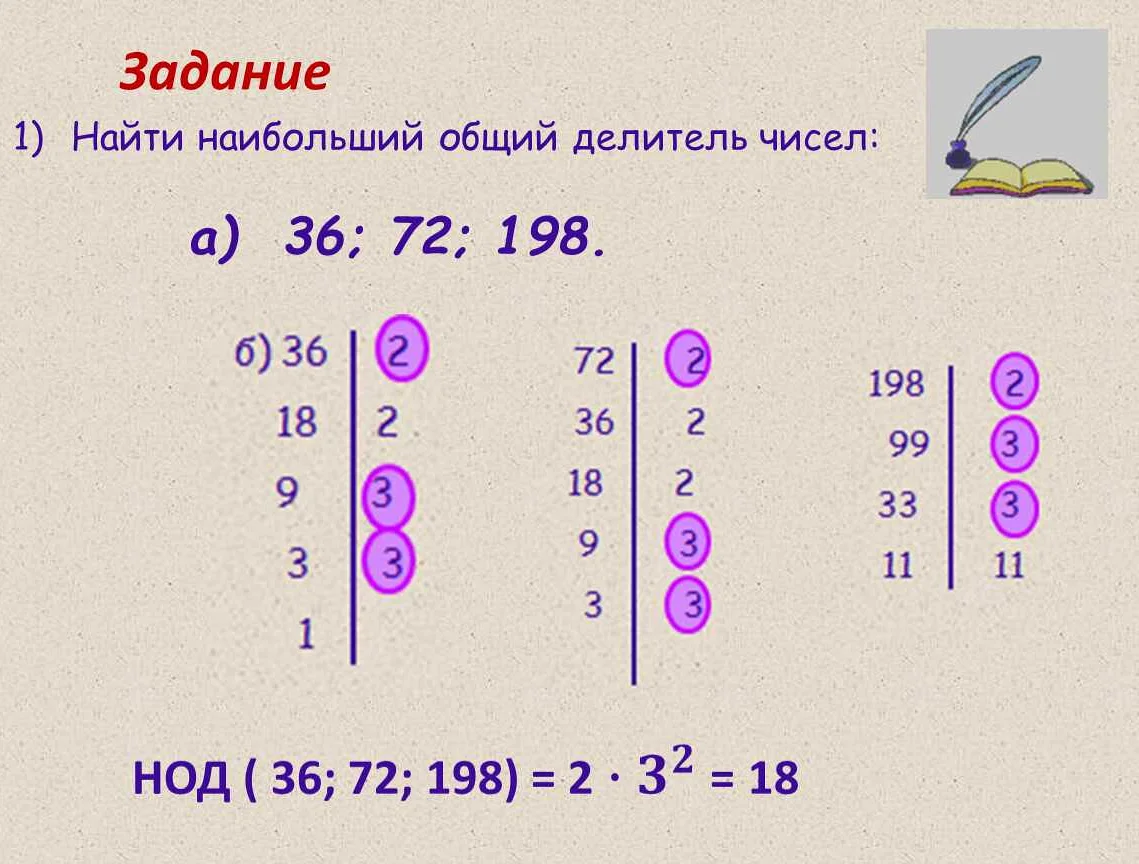
Нод (наибольший общий делитель) – это наибольшее число, на которое делятся без остатка два или более числа. Например, для чисел 12 и 16 наибольшим общим делителем будет число 4, так как оно делит оба числа без остатка, а большее число, например, 6, делит только одно число без остатка.

Формула для нахождения нода двух чисел a и b выглядит так: нод(a, b) = a % b, где % — оператор остатка от деления. То есть, наибольший общий делитель двух чисел равен остатку от деления первого числа на второе.

Нок (наименьшее общее кратное) – это наименьшее число, которое делится нацело на два или более числа. Например, для чисел 4 и 6 наименьшим общим кратным будет число 12, так как оно делится нацело и на 4, и на 6, и большее число, например, 18, делится только на одно число без остатка.

Формула для нахождения нока двух чисел a и b выглядит так: нок(a, b) = (a * b) / нод(a, b), где / — оператор деления. То есть, наименьшее общее кратное двух чисел равно произведению этих чисел, деленному на их наибольший общий делитель.

Основные понятия математики 6 класса

1. Числа и числовые выражения: в 6 классе ученики изучают различные виды чисел, такие как натуральные, целые, рациональные и иррациональные числа. Также они учатся работать с числовыми выражениями, выполнять операции сложения, вычитания, умножения и деления.

2. Десятичная система счисления: ученики узнают, как записывать числа в десятичной системе счисления, а также как выполнять операции с этими числами. Они также изучают понятие десятичной дроби и десятичного разложения числа.

3. Геометрия: в 6 классе ученики изучают основные понятия геометрии, такие как точка, прямая, отрезок, угол и многоугольник. Они также учатся строить геометрические фигуры и решать задачи на их основе.

4. Функции и графики: ученики знакомятся с понятием функции, ее графика и способами представления функций. Они учатся находить значения функций в заданных точках и строить графики функций.

5. Вероятность и статистика: ученики изучают основные понятия вероятности и статистики, такие как эксперимент, исход, вероятность события, выборка и диаграмма.

Изучение этих основных понятий поможет ученикам развить математическое мышление и подготовит их к более сложным темам в дальнейшем обучении.

Видео по теме:

Чем отличается нод от нок

Нод двух чисел является наибольшим числом, которое делит их без остатка. Например, для чисел 12 и 18, наибольший общий делитель равен 6, так как 6 делит оба числа без остатка.

Нок двух чисел является наименьшим числом, которое делится на оба числа без остатка. Например, для чисел 12 и 18, наименьшее общее кратное равно 36, так как 36 делится и на 12, и на 18 без остатка.

Таким образом, нод и нок имеют разные цели. Нод используется для нахождения общих делителей чисел, а нок — для нахождения общих кратных чисел. Они позволяют решать различные математические задачи и широко применяются в алгебре и арифметике.

Какие задачи решаются с помощью нод и нок

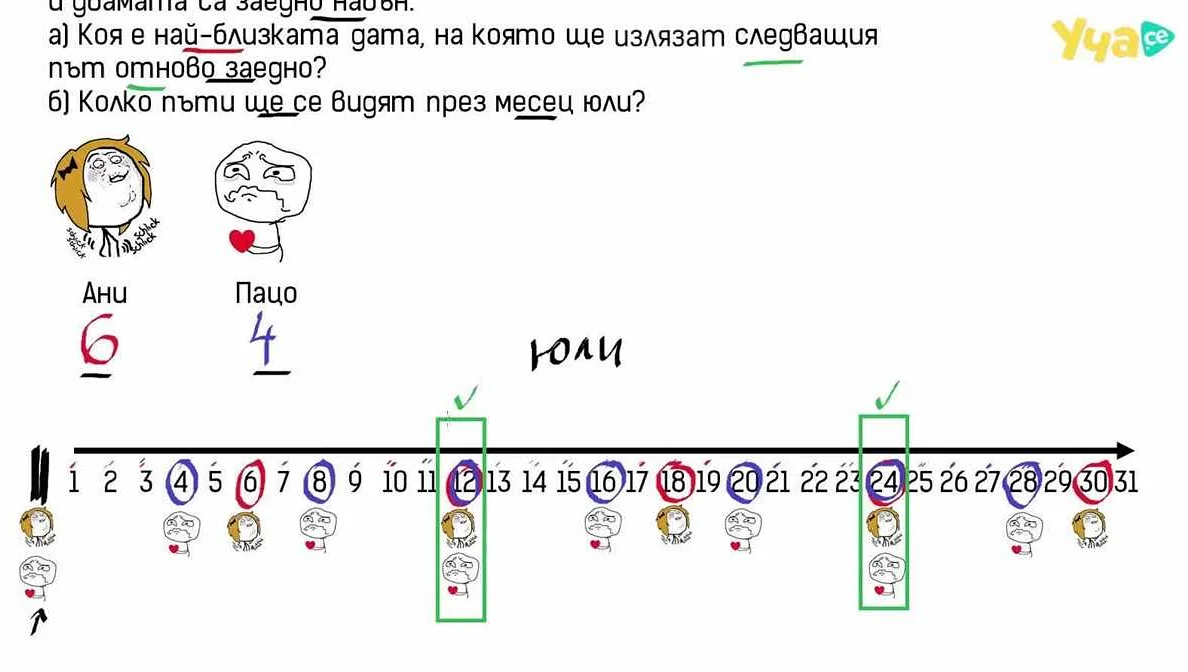
В математике, нод и нок используются для решения различных задач, связанных с нахождением общих множителей и общих кратных двух или более чисел.

Нод (наибольший общий делитель) используется для нахождения наибольшего числа, на которое делятся все заданные числа без остатка. Например, если нужно найти нод чисел 12 и 18, мы можем разложить их на простые множители: 12 = 2 * 2 * 3, 18 = 2 * 3 * 3. Затем, выбирая самое большое число из общих множителей, получим, что нод(12, 18) = 2 * 3 = 6. Нод также используется для упрощения дробей.

Нок (наименьшее общее кратное) используется для нахождения наименьшего числа, которое делится на все заданные числа без остатка. Например, если нужно найти нок чисел 4 и 6, мы можем разложить их на простые множители: 4 = 2 * 2, 6 = 2 * 3. Затем, учитывая все простые множители и их максимальные степени, получим, что нок(4, 6) = 2 * 2 * 3 = 12.

Использование нод и нок позволяет решать различные задачи, связанные с дробями, уравнениями, делением чисел на множители и другими математическими операциями.

Типичные примеры использования нод и нок

Пример использования нод:

Представим, что у нас есть граф, который описывает дорожную сеть города. В этом графе вершинами будут являться различные перекрестки и улицы, а ребрами — дороги, соединяющие эти перекрестки. Каждая вершина графа будет соответствовать конкретному перекрестку или улице, а нода — это название этой вершины. Например, нода «Площадь Ленина» будет соответствовать перекрестку, а нода «ул. Ленина» будет соответствовать улице с таким же названием.

Таким образом, использование нод позволяет наглядно описывать вершины графа и связи между ними.

Пример использования нок:

Если ноды описывают вершины графа, то ноки описывают ребра. Их можно рассматривать как связи между вершинами. Например, если у нас есть граф, описывающий дорожную сеть города, то ноки будут соответствовать дорогам между перекрестками. Например, нок «Дорога А» будет соответствовать дороге, соединяющей перекрестки «Площадь Ленина» и «Площадь Победы».

Таким образом, использование нок позволяет указывать связи между вершинами графа и определять, какие вершины достижимы друг из друга.

Как определить нод и нок в данной задаче

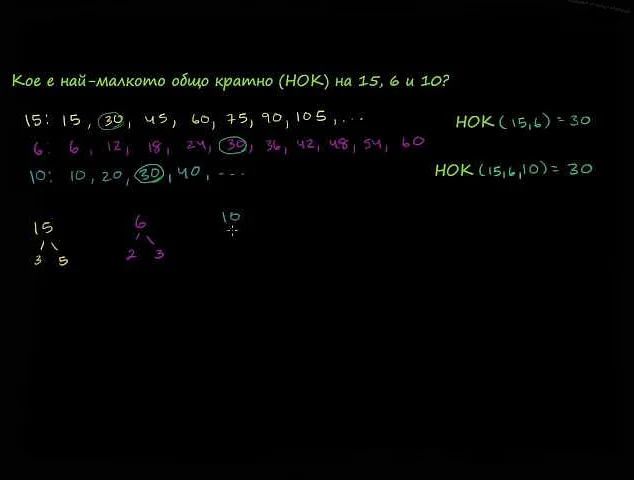
Нод (наибольший общий делитель) и нок (наименьшее общее кратное) двух чисел можно определить с помощью алгоритма Евклида.

Алгоритм Евклида заключается в последовательном делении большего числа на меньшее и нахождении остатка от деления. Операцию деления повторяют до тех пор, пока остаток от деления не станет равным нулю. На этом этапе число, на которое производится деление, является наибольшим общим делителем (нод).

Например, если даны числа 24 и 36, то алгоритм Евклида будет выглядеть следующим образом:

36 ÷ 24 = 1 (остаток: 12)

24 ÷ 12 = 2 (остаток: 0)

Таким образом, наибольший общий делитель (нод) чисел 24 и 36 равен 12.

Наименьшее общее кратное (нок) чисел можно определить с помощью формулы:

нок(a, b) = (a * b) / нод(a, b),

где a и b — числа, для которых ищется нок.

Продолжим пример с числами 24 и 36:

нод(24, 36) = 12,

нок(24, 36) = (24 * 36) / 12 = 72.

Таким образом, наименьшее общее кратное (нок) чисел 24 и 36 равно 72.

Правила работы с нод и нок

Правила для НОД:

1. НОД двух чисел всегда является положительным числом.
2. Если одно из чисел равно нулю, то НОД равен другому числу.
3. Если оба числа равны нулю, то НОД не определен.
4. НОД можно найти с помощью разложения чисел на простые множители и сравнения степеней простых множителей.
5. НОД можно найти с помощью алгоритма Евклида, который основан на последовательном делении одного числа на другое.

Правила для НОК:

1. НОК двух чисел всегда является положительным числом.
2. Если одно из чисел равно нулю, то НОК равен нулю.
3. Если оба числа равны нулю, то НОК не определен.
4. НОК можно найти с помощью разложения чисел на простые множители и сравнения степеней простых множителей.
5. НОК можно найти с помощью формулы: НОК = (a * b) / НОД(a, b), где a и b — два числа.

Правила работы с нод и нок помогут вам в решении задач и упрощении вычислений с числами.

Практические примеры на определение нод и нок

Чтобы лучше понять, в чем разница между наибольшим общим делителем (нод) и наименьшим общим кратным (нок), рассмотрим несколько примеров.

Пример 1:

Найдем нод и нок для чисел 12 и 18.

Делители числа 12: 1, 2, 3, 4, 6, 12

Делители числа 18: 1, 2, 3, 6, 9, 18

Наибольший общий делитель (нод) для чисел 12 и 18: 6

Наименьшее общее кратное (нок) для чисел 12 и 18: 36

Пример 2:

Найдем нод и нок для чисел 15 и 20.

Делители числа 15: 1, 3, 5, 15

Делители числа 20: 1, 2, 4, 5, 10, 20

Наибольший общий делитель (нод) для чисел 15 и 20: 5

Наименьшее общее кратное (нок) для чисел 15 и 20: 60

Пример 3:

Найдем нод и нок для чисел 24 и 36.

Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24

Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

Наибольший общий делитель (нод) для чисел 24 и 36: 12

Наименьшее общее кратное (нок) для чисел 24 и 36: 72

Таким образом, наибольший общий делитель (нод) — это наибольшее число, на которое делятся два заданных числа без остатка, а наименьшее общее кратное (нок) — наименьшее число, которое делится без остатка на оба заданных числа.

Использование нод и нок в решении математических задач

Нод двух чисел — это наибольшее число, которое одновременно делит оба этих числа без остатка. Например, нод чисел 12 и 18 равен 6. Нод часто используется при упрощении дробей, поиске простых чисел и решении диофантовых уравнений.

Нок двух чисел — это наименьшее число, которое делится на оба этих числа без остатка. Например, нок чисел 4 и 6 равен 12. Нок широко применяется при решении задач на временах, расстояниях и других задачах, связанных с периодичностью.

Использование нод и нок позволяет упрощать вычисления и находить общие закономерности в задачах. Знание этих понятий помогает ученикам лучше понимать математические процессы и четко формулировать решения задач.

В шестом классе ученики активно изучают нод и нок в рамках темы «Делители, кратные, нод и нок». Они учатся находить нод и нок различных чисел, применять их при решении задач и проводят анализ полученных результатов.

Использование нод и нок в решении математических задач помогает ученикам развивать логическое мышление, умение находить общие закономерности и применять их на практике. Освоение этих понятий является важным шагом в учебном процессе и дает возможность успешно справляться с более сложными математическими заданиями.

Вопрос-ответ:

Чем отличается нод от нок?

НОД (наибольший общий делитель) — это наибольшее число, которое одновременно делится на все заданные числа. НОК (наименьшее общее кратное) — это наименьшее число, которое одновременно делится на все заданные числа.

Как найти НОД и НОК двух чисел?

Чтобы найти НОД двух чисел, нужно найти все их общие делители и выбрать наибольший из них. Чтобы найти НОК, нужно найти все кратные числа каждого из заданных чисел и выбрать наименьшее из них.

Как найти НОД и НОК нескольких чисел?

Для нахождения НОД нескольких чисел нужно последовательно находить НОД каждых двух чисел и заменять два числа на полученный НОД до тех пор, пока не останется одно число — НОД всех заданных чисел. Для нахождения НОК нескольких чисел нужно последовательно находить НОК каждых двух чисел и заменять два числа на полученный НОК до тех пор, пока не останется одно число — НОК всех заданных чисел.

В чем заключается практическое применение НОД и НОК?

НОД и НОК имеют широкое применение в различных областях, таких как математика, физика, программирование и т.д. Они могут использоваться, например, для упрощения дробей, нахождения общего времени при синхронизации процессов, нахождения наименьшего общего кратного при работе с дробями и т.д.

Какие свойства есть у НОД и НОК?

У НОД и НОК есть несколько свойств. Например, для НОД справедливо свойство делимости (если число делится на НОД двух чисел, то оно делится и на сами числа). Для НОК справедливо свойство кратности (если НОК является кратным числам, то оно является кратным и каждому из этих чисел).