Что такое нод в математике и нок

Нод и нок — это два важных понятия в математике. Нод (наибольший общий делитель) и нок (наименьшее общее кратное) используются для решения различных задач, связанных с дробями, целыми числами и множествами. Узнайте, что такое нод и нок, как они вычисляются и как применяются в математике.

В математике термин «нод» (наибольший общий делитель) и «нок» (наименьшее общее кратное) являются ключевыми понятиями, используемыми при работе с числами. Нод и нок представляют собой важные инструменты, которые позволяют решать различные задачи, связанные с делением, разложением чисел на простые множители и поиском общих кратных.

Наибольший общий делитель (нод) двух или более чисел является наибольшим числом, которое одновременно является делителем для каждого из этих чисел. Наибольший общий делитель может быть найден различными методами, включая простое деление, разложение чисел на простые множители и алгоритм Евклида.

Наименьшее общее кратное (нок) двух или более чисел является наименьшим числом, которое делится на каждое из этих чисел без остатка. Наименьшее общее кратное также может быть найдено различными способами, включая простое умножение, разложение чисел на простые множители и использование алгоритма Евклида в сочетании с нахождением нода.

Примеры использования нода и нока в математике широко распространены. Они могут быть использованы для упрощения дробей, нахождения общего знаменателя, решения уравнений и систем уравнений, а также для поиска периодов в десятичных дробях. Знание понятия нода и нока является неотъемлемой частью математической грамотности и может быть полезным для решения различных задач в научных и инженерных областях.

Определение нод и нок

НОК (наименьшее общее кратное) — это наименьшее число, которое одновременно является кратным для двух или более чисел. То есть, НОК — это наименьшее число, которое делится на все заданные числа без остатка.

НОД и НОК являются важными понятиями в математике и широко применяются в различных областях, включая алгебру, арифметику и дискретную математику. Например, НОД используется для упрощения дробей, нахождения общего знаменателя, а также для решения уравнений и систем уравнений. НОК используется для определения периодичности и схожести временных интервалов, а также в задачах планирования и расписаний.

Свойства нод и нок

1. Нод — это точка, в которой производная функции равна нулю или не существует. В ноде меняется направление изменения функции.

2. Нок — это точка, в которой производная функции меняет знак, т.е. перескакивает через ноль. В ноке происходит смена выпуклости функции.

3. Ноды и ноки могут быть как локальными, так и глобальными. Локальные ноды и ноки находятся на ограниченных участках функции, в то время как глобальные ноды и ноки присутствуют на всей области определения функции.

4. Ноды и ноки могут быть стационарными или нестационарными. Стационарные ноды и ноки не изменяют свое положение с течением времени, а нестационарные ноды и ноки могут перемещаться.

Для наглядности рассмотрим пример: функция f(x) = x^2 — 4x + 3 имеет нод в точке x = 2 и нок в точке x = 1. В ноде происходит смена направления изменения функции, а в ноке происходит смена выпуклости функции.

Различия между нод и нок

Нод (наибольший общий делитель) двух чисел является наибольшим числом, которое делит оба числа без остатка. Нод используется для нахождения общих множителей и делителей чисел и может быть полезен при упрощении дробей, решении уравнений и других задачах.

Нок (наименьшее общее кратное) двух чисел является наименьшим числом, которое делится на оба числа без остатка. Нок используется для нахождения общих кратных чисел и может быть полезен при сложении и вычитании дробей, решении уравнений и других задачах.

Основное различие между нод и нок заключается в том, что нод находит наибольший общий делитель двух чисел, а нок находит наименьшее общее кратное двух чисел.

Для примера, рассмотрим два числа: 12 и 18. Нод этих чисел равен 6, так как 6 является наибольшим числом, которое делит и 12, и 18 без остатка. Нок этих чисел равен 36, так как 36 является наименьшим числом, которое делится и на 12, и на 18 без остатка.

ЧислаНодНок

12 и 18

6

36

Примеры использования нод и нок

Ноды и ноки используются в различных математических конструкциях и вычислениях. Вот несколько примеров:

Пример 1: В дереве вычислений ноды представляют операции, а ноки – операнды. Например, в выражении «2 + 3 * 4», ноды будут представлять операции «+» и «*», а ноки – числа «2», «3» и «4».

Пример 2: В графах ноды могут представлять вершины, а ноки – ребра. Например, в графе дорожной сети, ноды будут представлять перекрестки, а ноки – дороги, соединяющие эти перекрестки.

Пример 3: В бинарных деревьях ноды могут представлять узлы дерева, а ноки – значения, хранящиеся в каждом узле. Например, в бинарном дереве поиска, ноды будут представлять узлы дерева, а ноки – числа, которые хранятся в каждом узле.

Это лишь некоторые из примеров использования нод и нок в математике. Они могут быть применены в различных областях, от графов и деревьев до алгоритмов и вычислений.

Практическое значение нод и нок

Одним из основных практических значений НОД и НОК является их применение в задачах долей и пропорций. Например, при расчете различных соотношений, таких как смешивание разных веществ или разделение чего-либо на части, нод и нок могут помочь определить оптимальные пропорции и доли.

Также НОД и НОК находят применение в задачах календарного планирования. Например, при планировании мероприятий, длительность которых измеряется в разных временных единицах (например, часы и минуты), нод и нок позволяют определить общую длительность или наименьший общий множитель временных интервалов.

Кроме того, НОД и НОК находят применение в теории вероятности. Например, при решении задач на нахождение вероятности взаимозависимых событий, нод и нок могут помочь определить общую вероятность наступления событий.

В области информатики НОД и НОК широко используются при решении задач, связанных с работой с числами, их разложением на простые множители или сравнением их значений.

Таким образом, понимание и умение применять НОД и НОК в практических задачах является важным навыком, который может быть полезен в различных сферах деятельности.

Как найти нод и нок

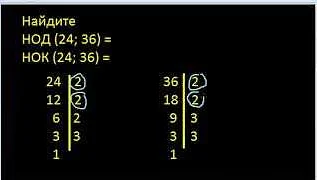
Нод (наибольший общий делитель) и нок (наименьшее общее кратное) двух чисел можно найти с помощью нескольких алгоритмов.

Алгоритм Евклида является одним из наиболее распространенных и простых способов нахождения нод двух чисел. Он основан на принципе, что наибольший общий делитель двух чисел равен наибольшему общему делителю их разности и одного из чисел. Применение алгоритма Евклида позволяет быстро и эффективно находить нод.

Алгоритм нахождения нок также может быть основан на алгоритме Евклида. Для нахождения нок двух чисел необходимо найти их нод и затем воспользоваться формулой: нок = (число1 * число2) / нод. Таким образом, нахождение нок сводится к нахождению нод и выполняется в несколько шагов.

Для наглядности и удобства вычислений можно использовать таблицу, в которой будут представлены шаги алгоритма Евклида для нахождения нод и нок. В таблице необходимо последовательно записывать числа, их разности и результаты деления, пока разность не станет равной нулю. На последнем шаге в таблице будет искомое значение нод (или нок).

Число 1Число 2РазностьНодНок

12	8	4
8	4	4
4	0	4

В данной таблице приведен пример вычисления нод и нок для чисел 12 и 8. Первый столбец содержит исходные числа, второй столбец — разности между числами, третий столбец — результаты деления. Последний ненулевой результат деления будет являться искомым значением нод (или нок).

Нод и нок в алгоритмах

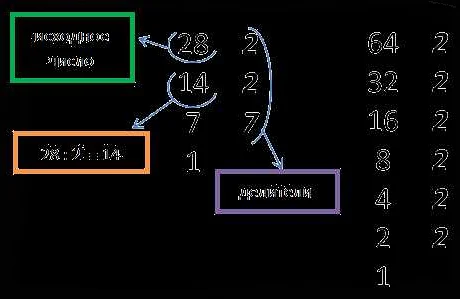
Нод двух чисел — это наибольшее число, которое делит оба числа без остатка. Например, для чисел 12 и 18, нод равен 6, так как это наибольшее число, которое делит и 12, и 18.

Нок двух чисел — это наименьшее число, которое делится на оба числа без остатка. Например, для чисел 4 и 6, нок равен 12, так как это наименьшее число, которое делится и на 4, и на 6.

Алгоритмы для нахождения нода и нока могут быть разными, но часто используются алгоритмы на основе разложения чисел на простые множители и алгоритмы Евклида. Алгоритм Евклида основан на том, что нод двух чисел равен ноду остатка от деления одного числа на другое и делителю. Этот алгоритм может быть реализован как рекурсивная функция или итеративный цикл.

Нод и нок имеют ряд свойств, которые могут быть использованы при решении арифметических задач. Например, для трех чисел A, B и C, нод(A, B, C) равен ноду(nod(A, B), C). Это свойство позволяет находить нод нескольких чисел путем последовательного нахождения нода двух чисел.

В заключение, понимание нода и нока в алгоритмах позволяет эффективно решать различные задачи, связанные с арифметикой и алгоритмами. Знание алгоритмов нахождения нода и нока помогает в решении проблемы нахождения наименьшего общего кратного, определения простых чисел и других задач, связанных с делением и разложением чисел.

Вопрос-ответ:

Что такое нод и нок в математике?

Нод (наибольший общий делитель) и нок (наименьшее общее кратное) — это два основных понятия в теории чисел. Нод двух чисел — это наибольшее число, на которое оба числа делятся без остатка. Нок двух чисел — это наименьшее число, которое делится на оба числа без остатка.

Как найти нод и нок двух чисел?

Нод можно найти с помощью алгоритма Евклида. Для этого нужно разделить одно число на другое и найти остаток. Затем нужно разделить предыдущее деление на полученный остаток и так далее, пока остаток не станет равным нулю. Нод будет равен последнему ненулевому остатку. Нок можно найти с помощью формулы: нок(a,b) = |a * b| / нод(a,b).

Какие свойства имеют нод и нок?

Нод двух чисел всегда является положительным числом и не превышает наименьшего из двух чисел. Нок двух чисел также всегда является положительным числом и не меньше наибольшего из двух чисел. Кроме того, нок двух чисел равен их произведению, если числа взаимно простые.

Какие примеры можно привести для нод и нок?

Примеры нод: нод(12, 18) = 6, нод(20, 30) = 10. Примеры нок: нок(4, 6) = 12, нок(15, 25) = 75. Также можно рассмотреть примеры, когда числа взаимно простые: нод(7, 9) = 1, нок(7, 9) = 63.

Для чего используются нод и нок в математике?

Нод и нок широко используются в различных областях математики, таких как теория чисел, алгебра, дискретная математика и др. Нод например, применяется для упрощения дробей, решения линейных диофантовых уравнений и поиска общих делителей. Нок используется, например, для нахождения общего кратного для периодических явлений и решении задач на временные интервалы.

Что такое нод и нок в математике?

НОД (наибольший общий делитель) и НОК (наименьшее общее кратное) — это два важных понятия в математике, относящихся к числам. НОД двух чисел — это наибольшее число, на которое оба числа делятся без остатка. НОК двух чисел — это наименьшее число, которое делится на оба числа без остатка.

Какие свойства имеют НОД и НОК?

НОД и НОК обладают несколькими важными свойствами. Например, свойство коммутативности означает, что порядок чисел в выражении НОД(a, b) или НОК(a, b) не имеет значения. То есть, НОД(a, b) = НОД(b, a) и НОК(a, b) = НОК(b, a). Еще одно свойство — ассоциативность, означает, что можно находить НОД или НОК более чем двух чисел в любом порядке, например, НОД(a, НОД(b, c)) = НОД(НОД(a, b), c). Другие свойства включают распределительные законы и свойства относительно умножения и деления.

Видео по теме: