Нод и нок в математике что это
Содержимое
- 1 Нод и нок в математике что это
- 1.1 Нод и нок в математике: понятие и определение
- 1.2 Нод и нок: различия и сходства
- 1.3 Нод и нок: основные свойства и принципы вычисления
- 1.4 Нод и нок: примеры из реальной жизни
- 1.5 Нод и нок: применение в различных областях
- 1.6 Видео по теме:
- 1.7 Вопрос-ответ:
- 1.8 Нод и нок: алгоритмы вычисления
- 1.9 Нод и нок: сложность вычисления и возможные оптимизации
Нод и нок (наибольший общий делитель и наименьшее общее кратное) — основные понятия в математике, используемые для нахождения общих свойств и операций над числами. Наибольший общий делитель (НОД) двух или нескольких чисел — это наибольшее число, которое одновременно делится на все эти числа. Наименьшее общее кратное (НОК) двух или нескольких чисел — это наименьшее число, которое делится на все эти числа без остатка. Узнайте, как эти понятия применяются в математике и как их можно вычислить.
Нод, или наибольший общий делитель двух чисел, является одной из важнейших арифметических операций. Он позволяет найти наибольшее число, которое одновременно делится на оба заданных числа без остатка.
Нод используется во множестве математических и инженерных задач. Например, он может быть использован для упрощения дробей, определения периодичности повторения десятичной дроби, построения простых чисел и т.д.
Для вычисления нода существует несколько методов, включая метод Эвклида и его расширенную версию. Основная идея метода Эвклида заключается в последовательном делении двух чисел, пока остаток не станет равным нулю. Нод будет равен последнему ненулевому остатку.
Нок, или наименьшее общее кратное двух чисел, является другой важной арифметической операцией. Он позволяет найти наименьшее число, которое делится на оба заданных числа без остатка.
Нок также находит применение во многих областях. Например, он может быть использован для вычисления времени периодического явления, определения взаимосвязи между двумя или более событиями, построения схем параллельной работы и т.д.
Для вычисления нока существует несколько методов, включая методы факторизации и решето Эратосфена. Основная идея метода факторизации заключается в разложении чисел на простые множители и умножении наименьших степеней этих множителей.
Нод и нок в математике: понятие и определение
НОД двух или более чисел — это наибольшее число, на которое делятся все эти числа без остатка. Например, НОД чисел 12 и 18 равен 6, так как оно делится и на 12, и на 18 без остатка, при этом нет другого числа, которое могло бы быть большим и делилось бы на оба этих числа.
НОК двух или более чисел — это наименьшее число, которое делится на все эти числа без остатка. Например, НОК чисел 4 и 6 равен 12, так как это наименьшее число, на которое без остатка делятся и 4, и 6.
Для вычисления НОД и НОК существует несколько способов. Один из самых распространенных методов для вычисления НОД — алгоритм Евклида. Он основан на том, что НОД двух чисел равен НОДу одного из них и остатка от деления второго числа на первое. Данный алгоритм может быть применен последовательно для вычисления НОД более чем двух чисел.
Для вычисления НОК существует несколько методов, включая метод разложения на простые множители и метод использования НОД. Метод разложения на простые множители сводит вычисление НОК к нахождению наименьшей общей степени всех простых множителей чисел. Метод использования НОД заключается в следующем: НОК двух чисел равен произведению самих чисел, деленному на их НОД.
ОперацияОбозначение
| НОД | gcd(a, b) |
| НОК | lcm(a, b) |
Нод и нок: различия и сходства
Различия:
- Нод используется для нахождения наибольшего общего делителя двух или более чисел, тогда как нок используется для нахождения наименьшего общего кратного.
- Нод можно вычислить с помощью алгоритма Евклида, который основан на последовательных делениях и нахождении остатков, тогда как нок вычисляется путем деления наименьшего числа на нод и умножения на другое число.
- Нод всегда является положительным числом, тогда как нок может быть как положительным, так и отрицательным числом, в зависимости от знаков исходных чисел.
Сходства:
- Оба понятия важны для решения задач, связанных с дробями, простыми и составными числами, а также для выполнения операций с дробями, десятичными числами и различными системами счисления.
- Использование нод и нок позволяет упростить математические выражения, провести сокращение дробей, а также определить, есть ли общие множители или кратные числа.
- Нод и нок являются фундаментальными понятиями в теории чисел и алгебре, и их знание позволяет более глубоко понять принципы и законы математики.
В заключение, нод и нок, несмотря на свои различия в целях и способах вычисления, имеют много общего и они оба играют важную роль в математике.
Нод и нок: основные свойства и принципы вычисления

Основные свойства НОД и НОК:
СвойствоОписание
| Коммутативность | НОД(a, b) = НОД(b, a) НОК(a, b) = НОК(b, a) |
| Ассоциативность | НОД(a, НОД(b, c)) = НОД(НОД(a, b), c) НОК(a, НОК(b, c)) = НОК(НОК(a, b), c) |
| Идемпотентность | НОД(a, a) = a НОК(a, a) = a |
| Делимость | Если a делится на b без остатка, то НОД(a, b) = b Если a и b делятся на c без остатка, то НОК(a, b) = c |
Принципы вычисления НОД и НОК:
- Для вычисления НОД и НОК двух чисел можно использовать алгоритм Евклида. Он основан на том, что НОД(a, b) равен НОД(b, a mod b), где «mod» — операция нахождения остатка от деления.
- Для вычисления НОК двух чисел можно использовать формулу: НОК(a, b) = (a * b) / НОД(a, b).
НОД и НОК широко применяются в различных областях математики и информатики, например, в алгоритмах сжатия данных, криптографии, решении уравнений и многих других задачах.
Нод и нок: примеры из реальной жизни
ПримерОписание
| 1 | Планирование расписания |
| 2 | Разделение ресурсов |
| 3 | Расчет времени доставки |
| 4 | Подбор размеров |
| 5 | Анализ данных |
1. Планирование расписания: НОД может использоваться для определения наименьшего общего интервала времени, в течение которого несколько событий должны произойти одновременно или последовательно. Например, при составлении расписания занятий в школе, НОД может помочь определить, через какие промежутки времени можно проводить определенные уроки, чтобы не возникало перекрытий.
2. Разделение ресурсов: НОК может использоваться для определения наименьшего общего кратного объема ресурса, необходимого для выполнения нескольких задач. Например, при разделении задач между несколькими работниками, НОК может помочь определить, через какие интервалы времени необходимо предоставлять ресурсы каждому работнику.
3. Расчет времени доставки: НОК может использоваться для определения наименьшего общего кратного времени, требуемого для доставки груза или выполнения задачи. Например, при расчете времени доставки почты или товаров, НОК может помочь определить, через какие интервалы времени можно осуществить доставку с минимальной задержкой.
4. Подбор размеров: НОД может использоваться для определения наибольшего общего делителя двух или более чисел, что может быть полезно при выборе оптимального размера для одежды, обуви или других предметов. Например, при выборе размера одежды, НОД может помочь определить, какие размеры соответствуют наиболее широкому диапазону людей.
5. Анализ данных: НОД и НОК могут использоваться в анализе данных для определения структуры и связей между наборами данных. Например, при анализе данных, связанных с финансами или экономикой, НОД и НОК могут помочь определить общие тренды, цикличность и сезонность.
Таким образом, НОД и НОК являются не только абстрактными математическими понятиями, но и полезными инструментами в реальной жизни. Их применение в различных областях помогает оптимизировать процессы, улучшать планирование и принимать эффективные решения.
Нод и нок: применение в различных областях

Одной из основных областей, где нод и нок находят применение, является алгебра. В алгебре нод используется для решения уравнений и систем уравнений. Он позволяет находить общие множители и делители, а также сокращать дроби до простейших видов. Нок, в свою очередь, применяется для нахождения общего кратного нескольких чисел, что может быть полезно, например, при работе с дробями и рациональными числами.
Другая область, где нод и нок широко используются, это теория чисел. Нод и нок помогают находить различные свойства чисел, такие как взаимная простота, сравнение чисел по модулю и т.д. Они также применяются в задачах нахождения простых чисел, факторизации чисел и построения псевдослучайных генераторов.
Нод и нок также находят применение в криптографии, где они используются для шифрования и дешифрования информации. Алгоритмы на основе нод и нок обеспечивают высокую степень защиты данных и позволяют создавать надежные шифры.
Кроме того, нод и нок применяются в теории графов, где они используются для нахождения кратчайших путей, построения деревьев и определения связности графа. Они также находят применение в теории игр, экономике, физике и других областях науки и техники.
Таким образом, нод и нок являются важными математическими понятиями, которые находят широкое применение в различных областях. Их использование позволяет решать разнообразные задачи и получать новые знания и результаты в науке и технике.
Видео по теме:
Вопрос-ответ:
Что такое НОД и НОК?
НОД (наибольший общий делитель) двух или более чисел — это наибольшее число, которое одновременно делится на все эти числа без остатка. НОК (наименьшее общее кратное) — это наименьшее число, которое делится на все эти числа без остатка.
Как вычисляется НОД двух чисел?
НОД двух чисел можно вычислить с помощью алгоритма Евклида. Сначала необходимо разделить большее число на меньшее и получить остаток. Затем нужно повторить эту операцию с полученным остатком и делителем. Процесс повторяется до тех пор, пока не будет получен ноль в качестве остатка. На этом этапе делитель будет являться НОДом исходных чисел.
Как вычисляется НОК двух чисел?
НОК двух чисел можно вычислить с помощью формулы: НОК(a, b) = |a * b| / НОД(a, b). Где a и b — исходные числа, а НОД(a, b) — наибольший общий делитель. Также можно использовать алгоритм Евклида для нахождения НОДа и затем применить формулу для НОКа.
Зачем вычислять НОД и НОК чисел?
Вычисление НОД и НОК чисел имеет множество практических применений. Например, они используются при упрощении дробей, при решении уравнений и систем уравнений, при построении и анализе графов, а также в различных алгоритмах и задачах комбинаторики. Они помогают находить общие свойства чисел и упрощают решение различных математических задач.
Нод и нок: алгоритмы вычисления

Для вычисления нод и нок существуют различные алгоритмы. Рассмотрим основные из них:
Алгоритм Евклида для вычисления нод
Алгоритм Евклида основан на следующем принципе: нод двух чисел равен ноду остатка от деления большего числа на меньшее число и меньшему числу. Процесс повторяется до тех пор, пока одно из чисел не станет равным нулю. В этом случае ненулевое число будет являться нодом.
Алгоритм Евклида может быть представлен в виде таблицы:
Число AЧисло BОстаток от деления A на B
| 54 | 24 | 6 |
| 24 | 6 | 0 |
В данном примере нод чисел 54 и 24 равен 6.
Алгоритм нахождения нок через нод
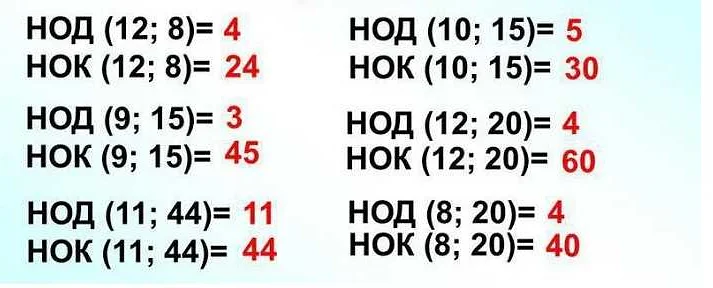
Для нахождения нок двух чисел можно использовать следующий алгоритм: нок равен произведению чисел, деленному на нод этих чисел. То есть, если A и B — два числа, то нок(A, B) = (A * B) / нод(A, B).
Например, если A = 4 и B = 6, то нод(4, 6) = 2, а нок(4, 6) = (4 * 6) / 2 = 12.
Таким образом, алгоритм нахождения нок через нод сводится к вычислению нод и простым арифметическим операциям.
Использование алгоритмов Евклида для вычисления нод и нахождения нок позволяет эффективно решать задачи, связанные с нахождением наименьшего общего делителя и наименьшего общего кратного чисел.
Нод и нок: сложность вычисления и возможные оптимизации

Сложность вычисления нод и нок зависит от используемого алгоритма. Один из наиболее распространенных алгоритмов вычисления нод — алгоритм Евклида. Он основан на принципе «деление с остатком» и позволяет быстро находить наибольший общий делитель двух чисел.
- Алгоритм Евклида для вычисления нод двух чисел:
- Если одно из чисел равно нулю, то нод равен другому числу.
- Иначе, повторяем шаги 3 и 4.
- Делим большее число на меньшее с остатком.
- Новое большее число — меньшее число, а новое меньшее число — остаток от деления.
- Повторяем шаги 3 и 4, пока новое меньшее число не станет равным нулю.
- Тогда нод равен последнему ненулевому остатку.
Сложность вычисления нода двух чисел с помощью алгоритма Евклида составляет O(log n), где n — максимальное из двух чисел. Это делает алгоритм очень эффективным даже для больших чисел.
Однако вычисление нока нескольких чисел может быть сложнее. Существует несколько способов оптимизации вычисления нока, например:
- Вычисление нока пары чисел и последующее использование полученного значения для вычисления нока с остальными числами.
- Использование формулы нока: нок(a, b) = |a * b| / нод(a, b).
- Использование алгоритма быстрого возведения в степень для более эффективного вычисления нока.
Все эти методы позволяют сократить количество операций и ускорить вычисление нока нескольких чисел.
Таким образом, вычисление нода и нока является важной задачей в математике. Алгоритм Евклида позволяет быстро находить нод двух чисел, а использование оптимизированных методов вычисления нока помогает ускорить работу с несколькими числами.



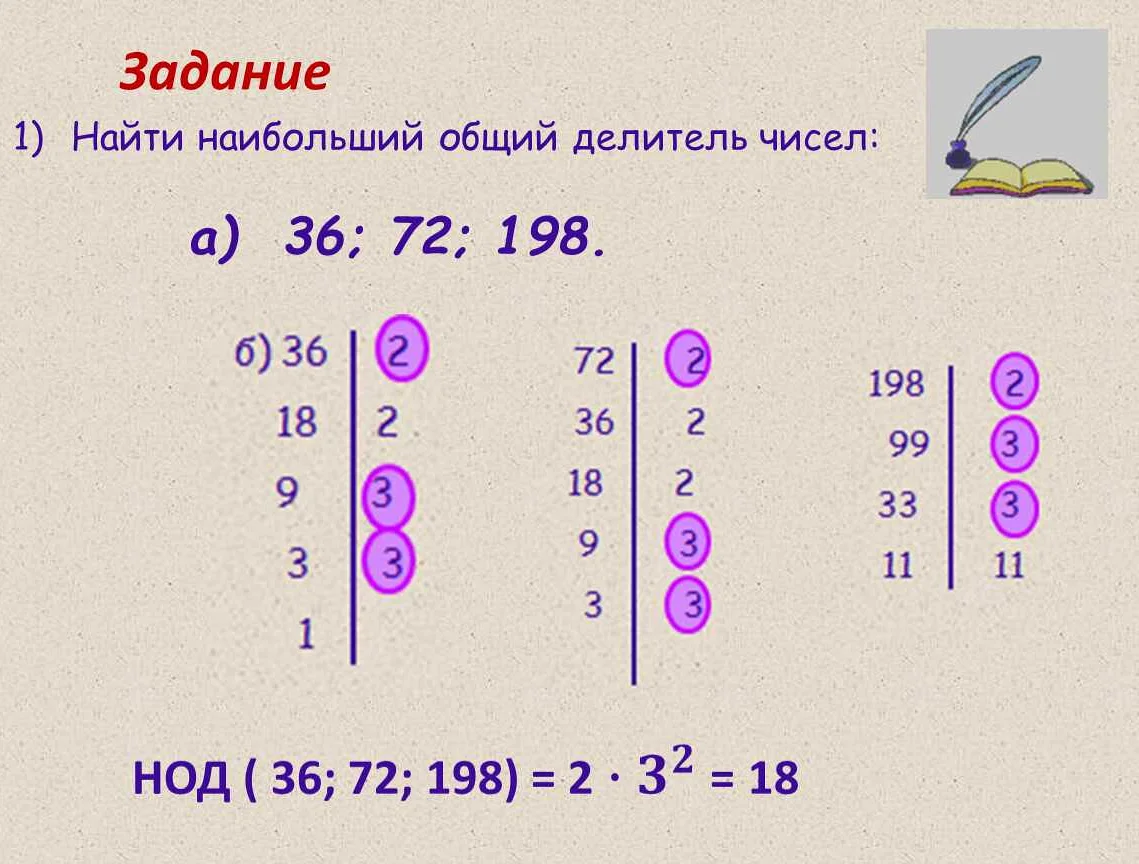
Отличная статья, очень понятно объясняет, что такое нод и нок в математике. Я давно интересуюсь этой темой, и мне очень пришлось по душе подробное описание алгоритма вычисления этих чисел. Всегда было непонятно, каким образом можно найти наибольший общий делитель двух чисел или наименьшее общее кратное. Теперь стало ясно, что это осуществимо через разложение чисел на простые множители. Этот метод вычисления очень логичный и эффективный. Спасибо автору за доступное изложение материала! Теперь я смогу использовать эту информацию в своих математических расчетах.
Отличная статья! Спасибо за разъяснение, что такое НОД и НОК. Я всегда слышал эти термины, но никогда не понимал, что они означают. Теперь я понял, что НОД — это наибольший общий делитель двух чисел, а НОК — это наименьшее общее кратное. Очень интересно узнать, как они вычисляются. Я не знал, что для вычисления НОД используется алгоритм Евклида, а для НОК — формула, основанная на НОД. Теперь я гораздо лучше понимаю, как решать задачи, связанные с нахождением НОД и НОК. Статья была очень понятной и информативной. Жду новых интересных материалов от вас!
Статья очень понятно и доступно объясняет понятия НОД и НОК. Математика всегда казалась сложной для меня, но благодаря этой статье я легко разобралась в этих понятиях. НОД — это наибольший общий делитель, а НОК — наименьшее общее кратное. Очень удобно знать, как вычислять эти значения, особенно при работе с дробями или различными единицами измерения. Спасибо автору за понятное объяснение и примеры. Теперь я чувствую себя более уверенной в решении математических задач!