Числитель что это такое в математике

Числитель — это математический термин, обозначающий числовую или количественную характеристику объекта или явления. Он используется в арифметике, алгебре и других разделах математики для обозначения числа или выражения, которое представляет собой отдельную единицу измерения или количество.

Числитель — это одна из основных составляющих дробей в математике. Он представляет собой верхнюю часть дроби и указывает на количество частей, на которые разделено целое число или объект. Числитель всегда должен быть целым числом и не может быть десятичным или отрицательным.

Определение числителя может быть проиллюстрировано простым примером. Рассмотрим дробь 3/4. Здесь число 3 является числителем, так как оно указывает на количество частей, которые мы берем из целого числа или объекта. В данном случае, мы берем 3 части из 4-х возможных.

Числитель имеет важное значение в математике, так как позволяет нам выражать нецелые числа и дроби. Он используется в различных областях математики, таких как арифметика, геометрия, алгебра и т. д. Например, в арифметике числитель используется для выполнения операций сложения, вычитания, умножения и деления с дробями.

Числитель в математике: что это?

Например, если у нас есть дробь 3/5, то числитель равен 3. Это означает, что мы берем 3 части из целого числа или объекта, которое разделено на 5 частей.

Числитель также может быть представлен в виде целого числа, если дробь является неправильной. Например, дробь 7/4 имеет числитель 7, что означает, что мы берем 7 частей из целого числа или объекта, которое разделено на 4 части.

Числитель в математике играет важную роль при работе с дробями и различными математическими операциями, такими как сложение, вычитание, умножение и деление дробей. Он помогает нам определить количество частей, которые мы берем из целого числа или объекта, и выполнять необходимые вычисления.

Важно помнить, что числитель всегда находится вверху дроби и указывает на количество частей, которые мы берем из целого числа или объекта.

Видео по теме:

Числитель в математике: основные свойства

Основные свойства числителя в математике:

Сложение числителей	Если имеются две или более дроби с одинаковыми знаменателями, числители могут быть сложены путем сложения числителей.
Вычитание числителей	При вычитании дробей с одинаковыми знаменателями, числители могут быть вычтены путем вычитания числителей.
Умножение числителей	При умножении дробей, числители перемножаются, а знаменатели перемножаются.
Деление числителей	При делении дробей, числитель первой дроби умножается на знаменатель второй дроби, а знаменатель первой дроби умножается на числитель второй дроби.

Числитель позволяет определить часть от целого числа или объекта. Он играет важную роль при работе с дробями и позволяет выполнять различные арифметические операции над ними. Понимание основных свойств числителя помогает в решении задач, связанных с дробями и их применением в реальных ситуациях.

Числитель в математике: арифметические операции

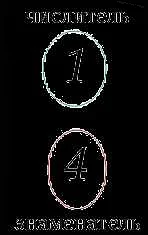
В математике числитель играет важную роль при выполнении арифметических операций над дробями. Рассмотрим основные арифметические операции с числителями:

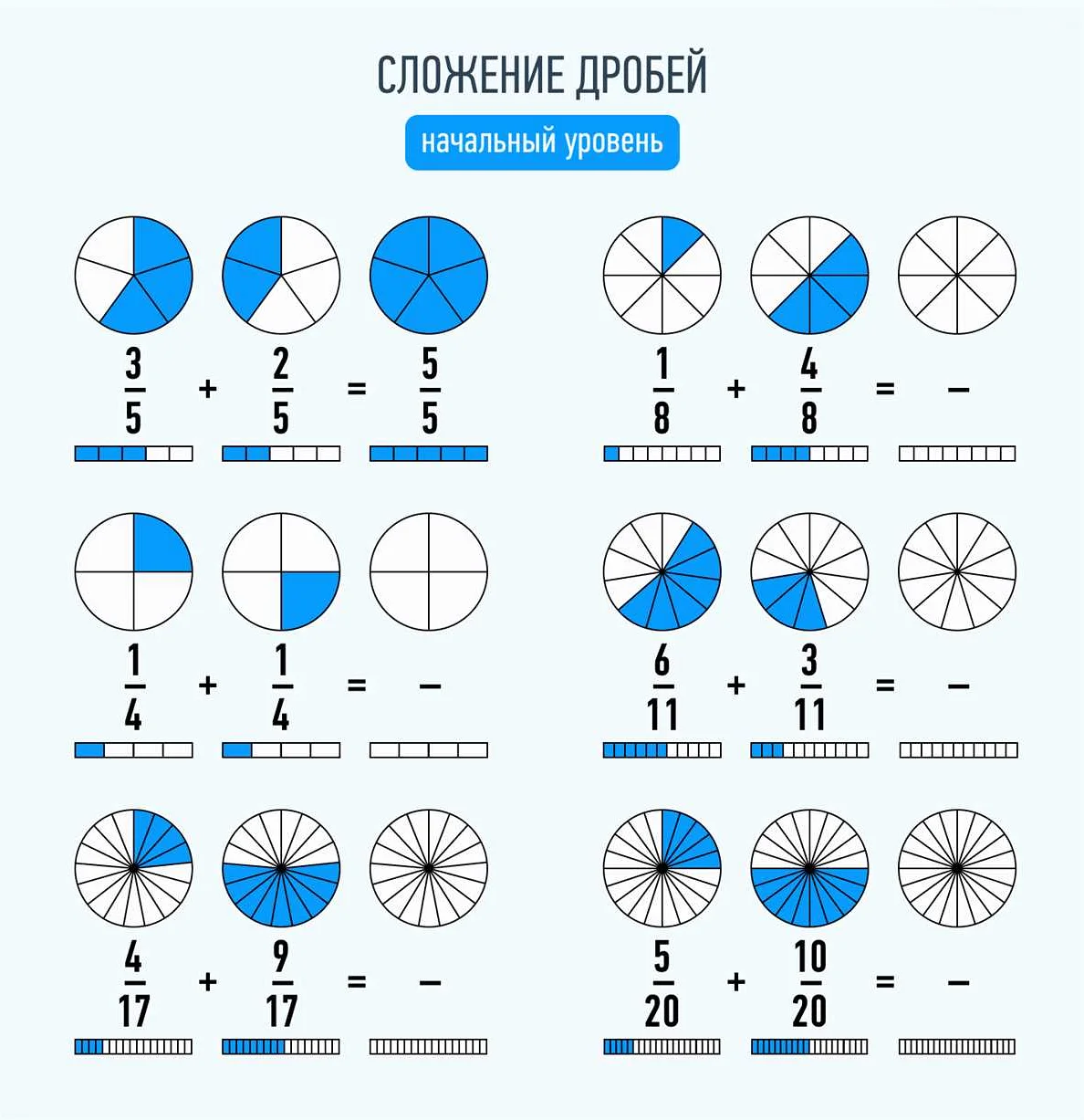
1. Сложение: Для сложения двух дробей с одинаковыми знаменателями нужно просто сложить их числители. Например, если у нас есть дроби 3/4 и 2/4, то их сумма будет 5/4. Если у дробей разные знаменатели, то для сложения их нужно привести к общему знаменателю.
2. Вычитание: Для вычитания двух дробей с одинаковыми знаменателями нужно просто вычесть их числители. Например, если у нас есть дроби 5/6 и 2/6, то их разность будет 3/6 или 1/2. Если у дробей разные знаменатели, то для вычитания их нужно привести к общему знаменателю.
3. Умножение: При умножении двух дробей нужно перемножить их числители. Например, если у нас есть дроби 2/3 и 1/4, то их произведение будет 2/12 или 1/6.
4. Деление: При делении одной дроби на другую нужно умножить первую дробь на обратную второй. Для этого нужно поменять местами числитель и знаменатель второй дроби. Например, если у нас есть дроби 3/5 и 2/7, то результат деления будет (3/5) * (7/2) = 21/10 или 2 1/10.

Таким образом, числитель в математике играет важную роль при выполнении арифметических операций с дробями. Знание и понимание этих операций позволяет более эффективно работать с дробями и решать задачи, связанные с их использованием.

Числитель в математике: десятичная система счисления

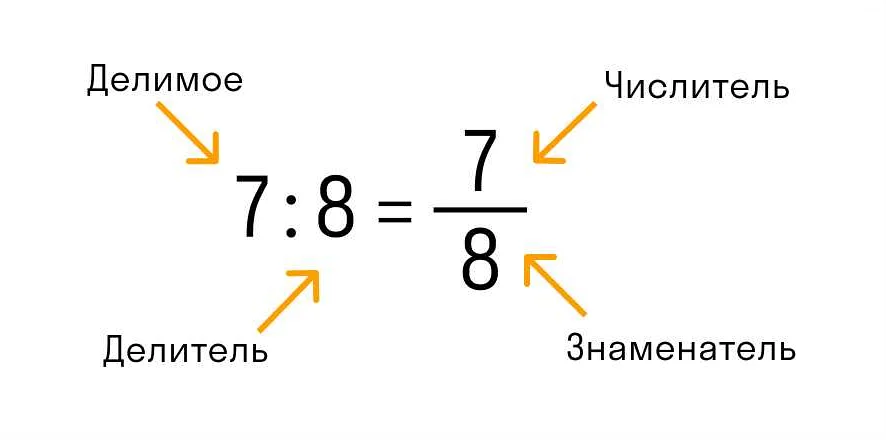
В десятичной системе счисления используются десять различных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Каждая цифра имеет свое место в числе, которое определяется разрядом. Например, число 257 состоит из трех разрядов: сотен, десятков и единиц.

В десятичной системе счисления число записывается слева направо, начиная с наибольшего разряда. Каждый разряд увеличивается в десять раз по сравнению с предыдущим разрядом. Так, число 257 можно разложить на разряды следующим образом:

СотниДесяткиЕдиницы

2

5

7

Таким образом, число 257 в десятичной системе счисления означает 2 сотни, 5 десятков и 7 единиц.

Десятичная система счисления широко используется в повседневной жизни, в том числе при работе с финансами, измерении времени и просто при подсчетах. Она является основной системой счисления в большинстве стран мира.

Числитель в математике: примеры использования

Рассмотрим несколько примеров использования числителя в математике:

1. Счет и арифметические операции:

Числитель используется для подсчета количества объектов. Например, если имеется 5 яблок, то число 5 является числителем, обозначающим количество этих яблок. Кроме того, числитель используется при выполнении арифметических операций, таких как сложение, вычитание, умножение и деление.

2. Дроби:

Числитель также применяется при работе с дробями. В дроби числитель обозначает количество частей, которые рассматриваем из целого. Например, в дроби 3/5 число 3 является числителем, обозначающим три части из пяти возможных.

3. Проценты:

Числитель часто используется при работе с процентами. Например, если имеется 25% скидка на товар, то число 25 является числителем, обозначающим количество процентов скидки.

4. Вероятность:

В теории вероятности числитель используется для указания количества благоприятных исходов в отношении к общему числу исходов. Например, если среди 10 марок почтовых марок 3 марки являются редкими, то число 3 является числителем, обозначающим количество редких марок.

Таким образом, числитель в математике играет важную роль при подсчете, измерении и описании количественных характеристик различных объектов и явлений.

Числитель в математике: рациональные числа

Рациональные числа могут быть положительными, отрицательными или нулем. Они могут быть представлены как десятичные дроби, но в этом случае они будут иметь конечное или периодическое представление.

Примеры рациональных чисел:

ЧислоОбыкновенная дробьДесятичная дробь

1	1/1	1.000…
-3	-3/1	-3.000…
2/3	2/3	0.666…
0	0/1	0.000

Рациональные числа обладают свойствами сложения, вычитания, умножения и деления, которые позволяют выполнять арифметические операции с этими числами. Они также могут быть сравнены и упорядочены друг с другом.

Рациональные числа играют важную роль в математике и широко применяются в различных областях, включая физику, экономику и инженерию.

Числитель в математике: иррациональные числа

Иррациональные числа могут быть представлены в виде бесконечных десятичных дробей, которые не имеют никакого периодического повторения. Некоторые из наиболее известных иррациональных чисел включают такие числа, как π (пи), e (число Эйлера) и корень квадратный из 2.

Числитель в иррациональных числах не может быть представлен в виде конечного числа или дроби. Например, числитель в числе π не может быть записан в виде конечной десятичной дроби или простой дроби. Он имеет бесконечное количество недостающих десятичных разрядов и не может быть точно представлен в виде десятичной дроби.

Иррациональные числа играют важную роль в математике и широко используются в различных областях, таких как физика, инженерия и компьютерные науки. Их свойства и связи с другими классами чисел изучаются в теории чисел и математическом анализе.

Иррациональные числа имеют множество интересных и важных свойств, и их изучение помогает расширить наше понимание числовой системы и ее приложений. Они представляют собой важную часть математического мира и оказывают влияние на множество аспектов нашей жизни.

Числитель в математике: применение в геометрии

Одним из примеров использования числителя в геометрии является нахождение длины отрезка. В геометрической системе координат, где точки представляются числами, длина отрезка может быть выражена числителем. Например, если на координатной прямой даны две точки с координатами 3 и 7, то длина отрезка между ними будет равна |7 — 3| = 4.

Также числитель может использоваться для нахождения площади прямоугольника. Если стороны прямоугольника обозначены числами a и b, то его площадь будет равна S = a * b. Здесь числитель представляет собой умножение двух чисел.

Еще одним примером применения числителя в геометрии является вычисление объема параллелепипеда. Если длина, ширина и высота параллелепипеда обозначены числами a, b и c соответственно, то его объем будет равен V = a * b * c. Таким образом, числитель здесь представляет собой умножение трех чисел.

В геометрии числитель играет важную роль при решении различных задач, связанных с измерением размеров и площадей фигур. Понимание его применения позволяет легче и точнее работать с геометрическими объектами и выполнять различные вычисления.

Вопрос-ответ:

Что такое числитель в математике?

Числитель — это одна из двух частей дроби, которая показывает, сколько частей целого имеется в дроби. Он находится над чертой дроби и обозначает количество, а ниже черты находится знаменатель, который показывает, на сколько частей целого делится дробь. Например, в дроби 3/4, числитель равен 3.

Какие примеры использования числителя в математике?

Числитель используется в математике для представления и описания долей и дробей. Например, когда мы хотим указать, что у нас есть три четверти от целого, мы можем записать это как дробь 3/4, где 3 — числитель. Также, числители используются при работе с пропорциями и при решении различных задач, связанных с долями и дробями.

Как найти числитель в десятичной дроби?

Для того чтобы найти числитель в десятичной дроби, нужно посмотреть на количество цифр после запятой. Например, в десятичной дроби 0,75 числитель равен 75, так как после запятой две цифры. Если в дроби нет запятой, то числитель равен самой десятичной дроби, так как она считается уже в виде десятичной части. Например, в дроби 0,5 числитель равен 0,5.

Как связаны числитель и знаменатель в дроби?

Числитель и знаменатель в дроби связаны путем определения количества частей целого. Числитель показывает, сколько частей целого имеется в дроби, а знаменатель показывает, на сколько частей целого делится дробь. Например, в дроби 3/4, числитель равен 3, что означает, что имеется 3 части целого, а знаменатель равен 4, что означает, что целое делится на 4 части.

Какие правила нужно знать для работы с числителем?

Для работы с числителем нужно знать некоторые правила. Например, когда складываются или вычитаются дроби с одинаковыми знаменателями, числители складываются или вычитаются, а знаменатель сохраняется. Также, при умножении дроби на число, числитель умножается на это число, а знаменатель остается неизменным. Правила работы с числителем зависят от конкретной операции и типа задачи.